最近在复习考研数学,对三重积分的球面坐标进行了学习,分享一下我对三重积分的球面坐标的基本理解。
1.球坐标的几何表示
直角坐标与球面坐标的关系如下:
其中,与
分别为OC与Z轴正方向的夹角,OC在XOY平面上与x轴正方向的夹角,通过下面这个图可以清晰得到球坐标
与直角坐标
之间的关系。

2.球坐标下的三重积分表达式
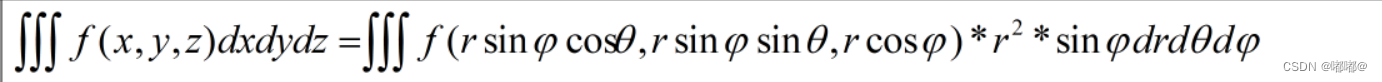
那么,这个球坐标下的三重积分表达式是怎么转换得到的呢?借用下面一张经典的图——

它的体积元素dv,可以看成一个小正方体,长宽高分别为,通过计算,可以得出如上的结果。
3.球坐标的基本计算
通过几个例子来进行计算分析:
例题1:

通过对积分域的基本判断,我们可以采用球坐标的三重积分进行计算,但是如果对目标式不进行简单变形,直接将z的球坐标带入进行计算难免麻烦,可以采用球的对称性的特点进行变化,起到简化计算的效果。

例题2:

首先对积分区域进行简单分析,它是由一个圆锥和一个半球体构成。

我们对积分域用球坐标进行计算。
首先,容易看出,积分域上点与z轴形成的夹角在45°与90°之间。接下来计算,r的范围。我们从o点引射线,如图——

计算得到:

于是计算得到——
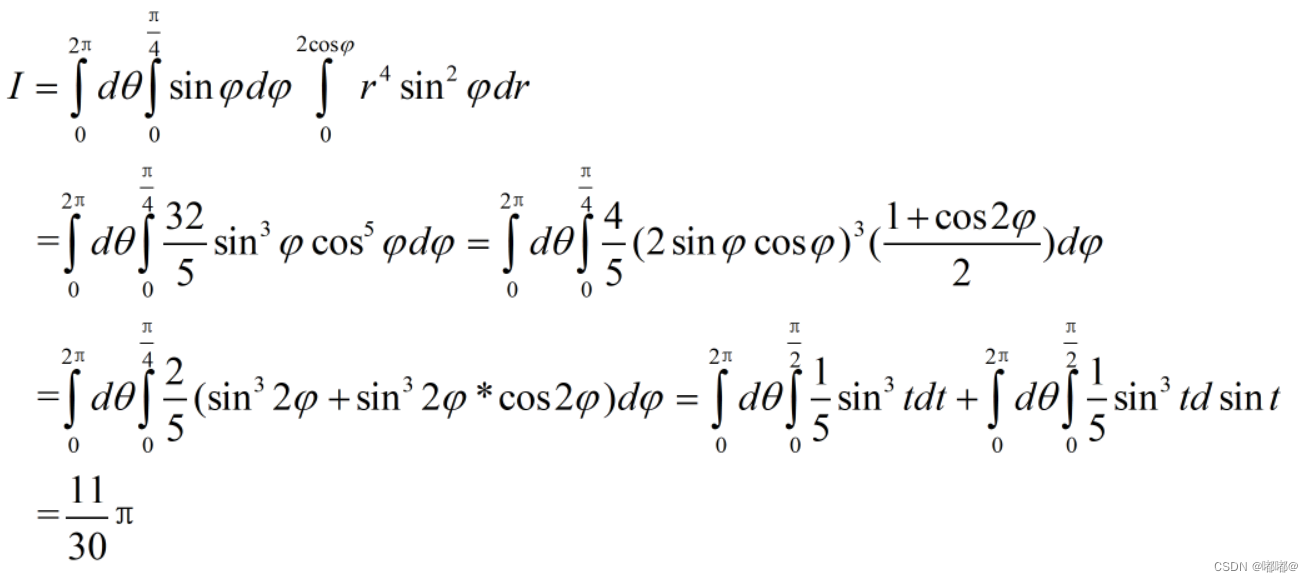























 879
879

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








