目录
一、电机理论基础
| 电机 | |||||||||
| 功率电机 | 控制电机 | ||||||||
| 直流电机 | 交流电机 | 交直两用电机 | 无刷直流电机 | 力矩电机 | 步进电机 | 伺服电机 | |||
1.异步电动机
异步电动机是一种交流电机,主要作为电动机使用。异步电机可以是三相的,也可以是单相的。三相异步电机主要用于工农业生产。单相异步电动则广泛用于各种民用电器和电动工具。
这里以三相交流异步电动机为例,讲解异步电机内部结构。三相异步电动机的基本结构主要由两部分组成:静止的定子和旋转的转子。定子与转子之间,留有相对运动所必需的空隙。图4-1是三相鼠笼式异步电动机的外形和内部结构。定子由定子铁芯、定子绕组、机座及端盖等组成。转子由转子铁芯、转子绕组和转轴组成。

2.直流有刷电机
直流有刷电机(BDC)是一种内含电刷装置,可以将直流电能转换成机械能的电动机。 在允许的范围之内,只需要调整电压,即可调整它的转速,因此这类电机拥有良好的调速性能。直流电机是指能通过直流电流而产生机械运动的电动机。
直流电机的结构形式很多,但总体上总不外乎由定子(静止部分)和转子(运动部分)两大部分组成。图4-3即为普通直流电机的结构图。直流电机的定子用于安放磁极和电刷,并作为机械支撑。它包括主磁极﹑换向极、电刷装置和机座等。转子一般称为电枢,主要包括电枢铁芯、电枢绕组、换向器等。

3.步进电机
步进电机是一种将电脉冲转化为角位移的执行机构。会商哲变抵时强悲步进电机由定子和转子组成。定子由硅钢片叠成,有一定数量的磁极和绕组。转子用硅钢片叠成或用软磁性材料做成凸极结构。如图4-12所示为一定子结构图。图4-13所示为一转子结构图。
电动机定子上有6个等分的磁极,相邻两个磁极间夹角为60°,相对的两个磁极组成一相。当某一绕组有电流通过,则该绕组的两个磁极立即形成N极.S极。每个磁极上各有5个均匀分布的矩形小齿。

4.舵机
舵机是一种“特殊”的直流电机,其构造不仅只有电机部分,而且还自带一个控制器,所以舵机本身就是一个闭环的控制系统(伺服系统)。 当我们给舵机发送指令信号时,它可以将指令信号变换为输出轴的角度并保持住,即便是负载发生了变化,它也能够进行自动调节。

5.无刷直流电机
无刷直流电机(Brushless Direct Current Motor,BLDCM)是一种不使用机械结构换向电刷而直接使用电子换向器的新型电机。这种电机在使用中有许多优点,比如:能获得更好的扭矩转速特性、高速动态响应、高效率、长寿命、低噪声﹑高转速、无换向火花、运行可靠和易于维护等。无刷直流电机被广泛用于日常生活用具、汽车工业、航空、消费电子、医学电子和工业自动化等装置和仪表。

更加宏观上分,我们也可以直接把电机分为定子部分和转子部分。
- 定子就是有线圈绕组,固定不动的部分;
- 转子就是电机旋转的部分,用于输出电机的转动和扭矩。
而进一步的,无刷电机可以分为内转子和外转子两种。
- 内转子无刷电机就是转子在内部;
- 外转子无刷电机就是转子在外面,我们常见的无刷电机。比如航模无刷电机,就是外转子无刷电机。

而直流无刷电机的驱动,就是依靠改变电机定子线圈的电流交变频率和波形, 在定子周围形成磁场, 驱动转子永磁体转动, 进而带动电机转起来。所以,想要让电机成功驱动,研究如何改变定子线圈的电流交变频率和波形就是我们的工作重点。
二、无刷电机驱动
1.六步梯形换相

2.FOC驱动
参考资料:DENGFOC文档
FOC通过输入电机力矩Iq,经过帕克逆变换求得Iα,Iβ,然后通过克拉克逆变换求得iA,iB,iC输出到电机中。

三、克拉克变换
三相sin状波形降级为二维平面内双变量Iα,Iβ形式。

1.克拉克变换基本形式

2.克拉克变换等幅值形式
论文或资料中的克拉克变换往往都会乘上一个系数:如(等幅值变换系数),或
(等功率变换系数)。

①克拉克变换等幅值证明
证明:当A输入-1A的电流时,根据基尔霍夫电流定律,iB、iC电流为A,通过克拉克变换计算得Iα为
。

所以为了让式子等辐值,即使得A相-1A时,反应在α轴上的电流也是-1A,我们就得乘上系数,使得iA=Iα。所以得到了克拉克变换的等幅值形式。
②克拉克变换等幅值推算
在推算式子中我们消去了变量iC,正是因为基尔霍夫电流定律的存在,我们只需要知道两相电流就能够求解得到第三相的电流,进而可以省去一相电流采集硬件。

四、克拉克逆变换
克拉克变换将三相电iA,iB,iC转换成二维坐标形式的Iα,Iβ。
克拉克逆变换则是将二维坐标Iα,Iβ再通过运算换为三相电iA,iB,iC。
1.克拉克等幅值形式逆变换

五、帕克变换
1.帕克变换数学模型
帕克变换将电机旋转的物理状态通过数学转换转变为Iα,Iβ。
三相线圈是实际三相电流的流动模型,通过在定子上建立α-β坐标系可转化出Iα,Iβ二维向量。然后在坐标系中叠加转子,当转子不动时Iα,Iβ是定值,但是当转子开始旋转后Iα,Iβ开始不断变化。
所以再建立一个随转子转动的Q-D坐标系。Q-D坐标系转动时与α-β坐标系构成的夹角θ就被称为电角度。所以知道电角度θ就很容易将Q-D坐标系上的值映射到α-β坐标系上。

2.帕克变换
将α-β坐标系映射到Q-D坐标系
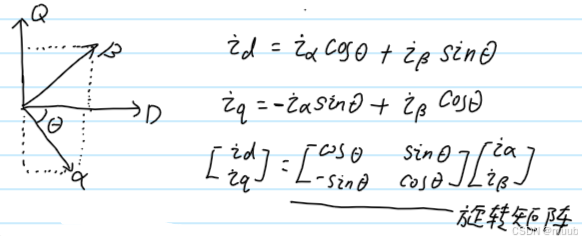
3.帕克逆变换

六、总结
将帕克变化拆分得到关于Iα,Iβ的关系式,式子中电角度θ是由编码器实时测出的所以已知,IQ,ID是有方向的矢量再加上电角度,所以可以看成为旋转的矢量。
通常在简单的FOC应用中,我们只需要控制IQ的电流大小,而把ID设置为0。此时,IQ的大小间接就决定了定子三相电流的大小,进而决定了定子产生磁场的强度。进一步我们可以说,它决定了电机产生的力矩大小。电机产生力矩后会绕中轴旋转,从而编码器读取的角度开始变化,然后新电角度再通过计算会得到新的IQ。
IQ是旋转的矢量,同时IQ又会间接影响磁场的强度,这正是FOC的名称磁场定向控制的由来。



























 2259
2259

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








