相关性分析

四种基本变量

1. 定类变量：能区分研究对象的属性，它只有类别层次之分，没有大小之分。比如性别(男，女)、职业(工人，白领)等等。
2. 定序变量：不仅能区分不同研究对象，还能反映出对象之间的高低、大小。比如满意度（非常满意、一般满意、满意、不满意）、文化程度（小学、初中、大学）。这些都是能看出高低的。
3. 定距变量：不仅能区分不同研究对象，反映出对象之间的高低，还能确定高低之差。它是没有绝对零点(取值为0代表没有)的。比如温度（10℃和20℃相差10℃）。
4. 定比变量：不同于定距变量的是：它具有绝对零点，也就是说可以反映出对象之间的倍数关系。比如身高（160cm是80cm的两倍），收入（收入90元是30元的三倍，收入为0代表没有收入）。
   层次关系：
   定类变量$\subset$定序变量$\subset$定距变量$\subset$定比变量

系数选择

系数	使用场景	正态性
Pearson相关系数	定距、定比变量，连续性变量	满足
Spearman相关系数	定序变量	不满足
Kendall相关系数	定序变量	不满足

由于上述都涉及到了正态性的判断，因此首先讲如何判断一个变量是否服从正态分布

后面要用的正态分布界值表放在网盘下面
百度网盘：正态分布界值表
提取码：mmca

正态性检验

KS检验

比较累计分布和理论分布或两个观测值分布的检验方法。
原假设$H_0$：两个观测值分布一致或数据符合理论分布
如果pvalue < $\alpha$， 拒绝原假设，若pvalue > $\alpha$，接受原假设

import pandas as pd
import scipy.stats as stats
#生成100个服从正态分布的随机数(不符合正态分布也可以)
X = np.random.normal(loc=0, scale=1, size=(100, ))

#KS检验
u = X.mean()
std = X.std()
#cdf可选很多。例如'norm', 'expon', 'rayleigh', 'gamma'，这里检验正态分布'norm'
stats.kstest(X, cdf="norm", args=(u, std))

'''
运行结果：(由于生成的是随机数，每次结果会不一样)
KstestResult(statistic=0.05967703844775221, pvalue=0.8474098341251864)
#说明：上述pvalue > 0.05，接受原假设，即服从正态分布
'''

夏皮洛-威尔克检验

适用小样本($3\le n\le 50$)
原假设和备择假设$H_0$：随机变量服从正态分布，$H_1$：随机变量不服从正态分布

#这里样本数100，其实超过了，但还是要演示一下
w = stats.shapiro(X)
w

'''
运行结果：
ShapiroResult(statistic=0.9812988042831421, pvalue=0.16760407388210297)
#说明：pvalue>0.05，说明接受原假设，即服从正态分布
'''

D’Agostino and Pearson omnibus normality test

推荐使用该用法，它是基于偏度和峰度计算的，具体详见python:5种正态性检验方法

#nan_policy默认为propagate，可选'raise'(返回空值), 'omit'(忽略空值)，表示如何处理空值
stats.normaltest(X, nan_policy='propagate')
'''
运行结果：
NormaltestResult(statistic=2.185353220985779, pvalue=0.3353177764064258)
#说明：pvalue>0.05，说明接受原假设，即服从正态分布
'''

安德森-达令检验

不仅可以检验正态分布，也可以检验指数分布、Logistic分布等其他分布

'''
参数选项：dist=['norm', 'expon', 'gumbel', 'extreme1', 'logistic']

返回值：
	statistic： 统计数,
	critical_values： 评判值,
	significance_level： 显著性水平(%)
	
说明：如果statistic < critical_values,则表示在相应的显著性水平下,接受原假设,认为符合给定的正态分布
'''

stats.anderson(X, dist="norm")
'''
运行结果：
AndersonResult(statistic=0.4699089092346611, critical_values=array([0.555, 0.632, 0.759, 0.885, 1.053]), significance_level=array([15. , 10. ,  5. ,  2.5,  1. ]))
#说明：假定我们选择显著性水平为5%,statistic<0.759,因此接受原假设，符合正态分布
'''

QQ图

这里不具体讲解数学公式，直接说结论：样本点是否落在一条直线上，直线斜率为标准差，截距为均值

fig, ax =plt.subplots(1, 1, figsize=(5, 5))
stats.probplot(X, plot=ax)
plt.show()

很直观的看出大部分样本点都在直线上，因此符合正态分布

直方图

画出直方图和核密度估计图观察是否符合正态分布

sns.distplot(X)
plt.show()

从图中可以看出符合正态分布
但如果变量不符合正态分布，那么如何将非正态分布转化为正态分布：

1. 对数变换
2. 平方根变换
3. 倒数变换

具体可以参考非正态分布数据转换为正态分布的几种方法

Pearson相关系数

$$\begin{gathered} \bar{X}=\frac{{\sum }_{i=1}^n{X}_i}{n},\bar{Y}=\frac{{\sum }_{i=1}^n{Y}_i}{n} \\ Cov(X,Y)=\frac{{\sum }_{i=1}^n(X-\bar{X})(Y-\bar{Y})}{n-1} \\ {\sigma }_X=\sqrt{\frac{{\sum }_{i=1}^n(X_i-\bar{X}{)}^2}{n-1}} \\ {\sigma }_Y=\sqrt{\frac{{\sum }_{i=1}^n(Y_i-\bar{Y}{)}^2}{n-1}} \\ r=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{{\sum }_{i=1}^n(X-\bar{X})(Y-\bar{Y})}{\sqrt{{\sum }_{i=1}^n(X_i-\bar{X}{)}^2}\sqrt{{\sum }_{i=1}^n(Y_i-\bar{Y}{)}^2}} \\ =\frac{1}{n-1}\sum _{i=1}^n(\frac{X_i-\bar{X}}{{\sigma }_X})(\frac{Y_i-\bar{Y}}{{\sigma }_Y}) \end{gathered}$$
最后一个式子可以看作X、Y标准化后的样本协方差

适用场景
1、连续变量
2、服从正态分布或接近正态分布
3、两变量是线性相关的（这点尤为重要，可以通过画散点图查看）

|r|的取值范围	相关程度
0.00-0.19	极低相关
0.20-0.39	低度相关
0.40-0.69	中度相关
0.70-0.89	高度相关
0.90-1.00	极高相关

注意： 1.非线性相关性也会导致相关系数很大 2、异常值和离群值都会影响相关系数 3、相关系数为0只能说不呈线性相关`，可能是非线性相关

假设检验：
原假设$H_0$：$r=0$，$H_1$：$r\ne 0$
构造统计量$t=r\sqrt{\frac{n-2}{1-r^2}}$，$t$服从自由度为n-2的t分布
计算$t$后查表或计算对应的p值判断是否显著
1、$|t|>t_{\frac{\alpha }{2}}$或 $p<\alpha$，表明r是显著
2、$|t|\le t_{\frac{\alpha }{2}}$或 $p\ge \alpha$，表明r是不显著
其中$\alpha =0.05$，在T分布表中可以查找

例子
来源皮尔逊（pearson）相关系数
下面是一组新生儿出生时身高和体重的数据，并计算他们之间的pearson相关系数

第一种方式

X = np.array([3.63, 3.02, 3.82, 3.42, 3.59, 2.87, 3.03, 3.46, 3.36, 3.3]) #体重
Y = np.array([53.1, 49.7, 48.4, 54.2, 54.9, 43.7, 47.2, 45.2, 54.4, 50.4]) #身高
r, p = stats.pearsonr(X, Y)
print(f"pearson系数: {r}")
print(f"pvalue: {p}")
'''
运行结果:
	pearson系数: 0.470177232968403
	pvalue: 0.1702861900753641
说明：pvalue > alpha=0.05的，所以算出的r是不显著的，即不存在线性相关
'''

或者你也可以自己实现

#计算协方差
def Cov(X, Y):
    X_avg, Y_avg = X.mean(), Y.mean()
    x, y = X - X_avg, Y - Y_avg
    return np.dot(x, y) / len(X)

pearson = Cov(X, Y) / (X.std() * Y.std())
pearson
'''
运行结果:0.4701772329684029
'''

t检验

t = pearson * np.sqrt((len(X)-2)/(1-pearson**2))
t
'''
运行结果：1.5068028555047277
'''

查找T分布表中$n^{\prime }=m-2=8,p(2)=0.05$所对应的t值，这里$n^{\prime }=38$，查找出t=2.306，1.506<2.306，也得出r是不显著的

Spearman相关系数

定义X和Y为两组定量数据，其Spearman系数为：
$$r_s=1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n(n^2-1)}$$
其中$d_i表示$X和Y之间的等级差
一个数的等级，就是所属列从小到大排序后其所处的位置，如果存在数组相同，取他们等级的平均值作为等级数

举个例子，来源于斯皮尔曼相关系数及其显著性检验

这里先给出身高和睡眠时间的等级，由于身高中含有两个160，并且他们的等级原本应该排在第三和第四，平均下来就是3.5，因此用3.5作为他们的等级数。同理也可得睡眠时间的等级，做差（身高的等级-睡眠时间的等级）得出等级差。

假设检验：
分为小样本($n\le 30$)和大样本($n>30$)两种情况

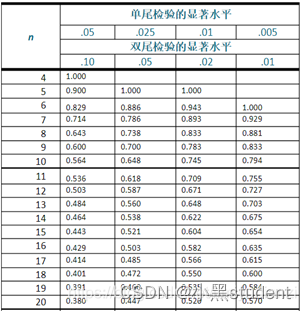
1. 小样本情况
   原假设$H_0$：$r_s=0$，$H_1$：$r_s\ne 0$
   构造统计量$t=r_s\sqrt{\frac{n-2}{1-r_s^2}}$，$t$服从自由度为n-2的t分布
   计算$t$后查表或计算对应的p值判断是否显著
   1、$|t|>t_{\frac{\alpha }{2}}$，表明$r_s$是显著
   2、$|t|\le t_{\frac{\alpha }{2}}$，表明$r_s$是不显著
   一般地，$\alpha =0.05$
   
2. 大样本情况
   $r_s\sqrt{n-1}\sim N(0,1)$
   需要计算出检验值$r_s\sqrt{n-1}$,并找出对应的p值（查标准正态分布界值表）
   $p\ge 0.05$，表明$r_s$没有显著性差异，即没有相关性
   $p<0.05$，表明$r_s$有显著性差异

依旧使用上面身高和睡眠时间的例子

X = np.array([160, 168, 174, 141, 160, 159, 176])
Y = np.array([7.6, 8.0, 8.8, 7.5, 6.9, 8.9, 9.0])
rs, p = stats.spearmanr(X, Y)
print(f"spearman相关系数： {rs}")
print(f"p_value： {p}")
'''
运行结果：
spearman相关系数： 0.5405624776173354
p_value： 0.21028925349550293
'''

上述的p值大于0.05了，我们就可以说$r_s$没有显著性差异，即无相关性

Kendall相关系数

参考自肯德尔（Kendall）相关系数概述及Python计算例
kendall系数分析的目标对象是定序变量

一致对: $(x_2-x_1)(y_2-y_1)\ge 0$
分歧对: $(x_2-x_1)(y_2-y_1)<0$

Kendall有两个计算公式，一个是Tau-a，它假定原数据中不存在并排；另一个是Tau-b，它可以处理相同值（并排）的情况
Tau-a=$\frac{2}{n(n-1)}(c-d)$,
Tau-b=$\frac{c-d}{\sqrt{(c+d+t_x)(c+d+t_y)}}$(比较常用的)
$c,d$分别表示一致对和分歧对的个数
$t_x,t_y$分别表示X、Y中并排的个数

适用条件：
1、两变量是两个连续变量，或两变量是两个有序分类变量，或一个有序分类变量一个连续变量。
2、两变量应当是配对的
3、变量之间存在单调关系

假设检验：
参考自Kendall’s tau-b相关性分析（具体的就不写了，等我再研究以下）
1、 $p<\alpha$，表明$\tau$是显著
2、 $p\ge \alpha$，表明$\tau$是不显著
这里也是通过查标准正态分布界值表得出p值

X = np.array([3, 5, 1, 6, 7, 2, 8, 8, 4])
Y = np.array([5, 3, 2, 6, 8, 1, 7, 8, 4])

stats.kendalltau(X,Y)
'''
运行结果：
KendalltauResult(correlation=0.6857142857142857, pvalue=0.011424737055271894)
'''

点双列相关

两变量中一个是连续变量，一个是二分类变量

$$r_{pb}=\frac{{\bar{X}}_p-{\bar{X}}_q}{S_x}\sqrt{pq}$$
p：二分类变量中某一类的占比
q：二分类变量中另一类的占比
${\bar{X}}_p$：p对应那类的连续变量的均值
${\bar{X}}_q$：q对应那类的连续变量的均值
点二系列相关绝对值越接近1，则二分类别变量和连续变量越相关

例子
来源点双列相关
某次测验中10名考生的一道单项选择题得分和其卷面总分如下表所示，试求该单项选择题的区分度。

考生	A	B	C	D	E	F	G	H	I	J
选择题得分	1	0	1	1	0	1	1	0	1	0
卷面总分	76	58	74	67	65	68	71	69	66	61

X = np.array([[1, 76], [0, 58], [1, 74], [1, 67], [0, 65], [1, 68], [1, 71], [0, 69], [1, 66], [0, 61]])

#计算样本标准差
def cal_std(X):
    mean = X.mean()
    std = np.sqrt(sum((X - mean) ** 2) / (len(X)-1))
    return std

Xp = X[X[:, 0]==1]
Xq = X[X[:, 0]==0]

p = len(Xp) / len(X)
q = 1 - p

Xp_mean = Xp[:, 1].mean()
Xq_mean = Xq[:, 1].mean()

r_pb = (Xp_mean - Xq_mean) / St * np.sqrt(p * q)
r_pb
'''
运行结果：0.6329667843516126
#说明：单选题与卷面总分中度相关，选择题得了分的卷面总分普遍比没得分的要高
'''

总结：
本文主要讲了四种相关性分析：Pearson系数、Spearman系数、Kendall系数和点双列相关。具体的使用要根据实际情况选择合适的相关性分析方法