【应用回归分析】CH3 回归参数的估计2——最小二乘估计的性质

最新推荐文章于 2023-09-13 13:15:32 发布

管理学phd

最新推荐文章于 2023-09-13 13:15:32 发布

阅读量2.3k

点赞数

分类专栏：应用回归分析文章标签：回归数据挖掘人工智能

本文链接：https://blog.csdn.net/m0_72318954/article/details/127340039

版权

本文深入探讨了最小二乘估计在回归分析中的重要性，详细阐述了其无偏性和方差最小化的特性。通过定理3.2.1、3.2.2和推论3.2.1，证明了最小二乘估计是最佳线性无偏估计，并解释了判定系数（R²）在评估模型拟合度中的作用。此外，还讨论了在误差向量服从正态分布时，最小二乘估计的更多优良性质。

摘要由CSDN通过智能技术生成

前言

无论从理论上还是从应用上，最小二乘估计都是最重要的估计，其原因是这种估计具有许多优良性质。

一、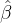 $\hat{\beta }$ 的性质

1.【定理3.2.1】

（1）内容

对于线性回归模型 $(3.1.6)$ ，最小二乘估计 $\hat{\beta }=(X^{'}X)^{-1}X^{'}y$ 具有下列性质

$(a)$ $E(\hat{\beta})=\beta$
$(b)$ $Cov(\hat{\beta})=\sigma^2(X^{'}X)^{-1}$

（2）证明

${\color{Blue} proof:}$

${\color{Blue} Ey=E(X\beta+e)=X\beta\Rightarrow E(\hat{\beta})=(X^{'}X)^{-1}X^{'}E(y)=(X^{'}X)^{-1}X^{'}X\beta=\beta}$

${\color{Blue} Cov(y)=Cov(X\beta+e)=Cov(e)=\sigma^2 I\Rightarrow Cov(\hat{\beta})=Cov[(X^{'}X)^{-1}X^{'}y]=(X^{'}X)^{-1}X^{'}\sigma^2 IX(X^{'}X)^{-1}=\sigma^2(X^{'}X)^{-1}}$

（3）定理说明

这个定理的第一条结论表明，最小二乘估计 $\hat{\beta }$ 是 $\beta$ 的无偏估计，这就是说，我们的估计没有系统性偏差。在实际问题中当我们用 $\hat{\beta }$ 去估计 $\beta$ 时，有时可能会偏高，有时则可能会偏低，但这些正负偏差在概率上平均起来等于零。

2.【推论3.2.1】

（1）内容

设 $c$ 为 $p*1$ 常数向量，对于线性函数 $c^{'}\beta$ ，我们称 $c^{'}\hat{\beta}$ 为 $c^{'}\beta$ 的最小二乘估计。

$(a)$ $E(c^{'}\hat{\beta})=c^{'}\beta$
$(b)$ $Cov(c^{'}\hat{\beta})=\sigma^2 c^{'}(X^{'}X)^{-1}c$

（2）推论说明

对任意的线性函数 $c^{'}\hat{\beta}=c^{'}(X^{'}X)^{-1}X^{'}y$ ，最小二乘估计 $c^{'}\hat{\beta}$ 是 $c^{'}\beta$ 的无偏估计，且方差为 $\sigma^2 c^{'}(X^{'}X)^{-1}c$ 。我们知道 $c^{'}\hat{\beta }=c^{'}(X^{'}X)^{-1}X^{'}y$ 是观测值 $y_{1},y_{2},\cdots,y_{n}$ 的线性函数，于是 $c^{'}\hat{\beta}$ 是 $c^{'}\beta$ 的一个具有无偏性的线性估计。当然我们还可以构造出 $c^{'}\beta$ 的许多其它的线性无偏估计，构成 $c^{'}\beta$ 的线性无偏估计类。我们的问题是，最小二乘估计 $c^{'}\hat{\beta}$ 在这个类中有什么特别的优良性呢？

3.【定理3.2.2】

（1）内容

（ $Gauss-Markov$ ）对于线性回归模型 $(3.1.6)$ ，在 $c^{'}\beta$ 的所有线性无偏估计中，最小二乘估计 $c^{'}\hat{\beta}$ 是唯一具有最小方差的估计。

（2）证明

${\color{Blue} proof:}$

设 $a^{'}y$ 是 $c^{'}\beta$ 的任意一个线性无偏估计，于是 $c^{'}\beta=E(a^{'}y)=a^{'}X\beta$ ，此式对一切 $p*1$ 向量 $\beta$ 都成立，因而必然有 $a^{'}X=c^{'}(3.2.1)$ 。因为 $Var(a^{'}y)=\sigma^2 a^{'}a=\sigma^2\left \| a \right \|^2$ ，对 $\left \| a \right \|^2$ 作分解：

$c^{'}\hat{\beta}=c^{'}(X^{'}X)^{-1}X^{'}y=(X(X^{'}X)^{-1}c)^{'}y$

$\left \| a \right \|^2=\left \| a-X(X^{'}X)^{-1}c+X(X^{'}X)^{-1}c \right \|^2=\left \| a-X(X^{'}X)^{-1}c\right \|^2+\left \| X(X^{'}X)^{-1}c\right \|^2+2c^{'}(X^{'}X)^{-1}X^{'}(a-X(X^{'}X)^{-1}c)(3.2.2)$