目录
一、费希尔判别的基本思想
费希尔判别的基本思想是投影(或降维),用p维向量的少数几个线性组合(称为费希尔判别函数或典型变量)
(一般r明显小于p)来代替原始的p个变量
,以达到降维的目的,并根据这r个判别函数
对样品的归属作出判别或将各组分离。成功的降维将使样品的归类或组的分离更为方便和有效,并且可以对前两个或前三个判别函数作图,从直观的几何图形上区别各组。
一个说明性的例子。
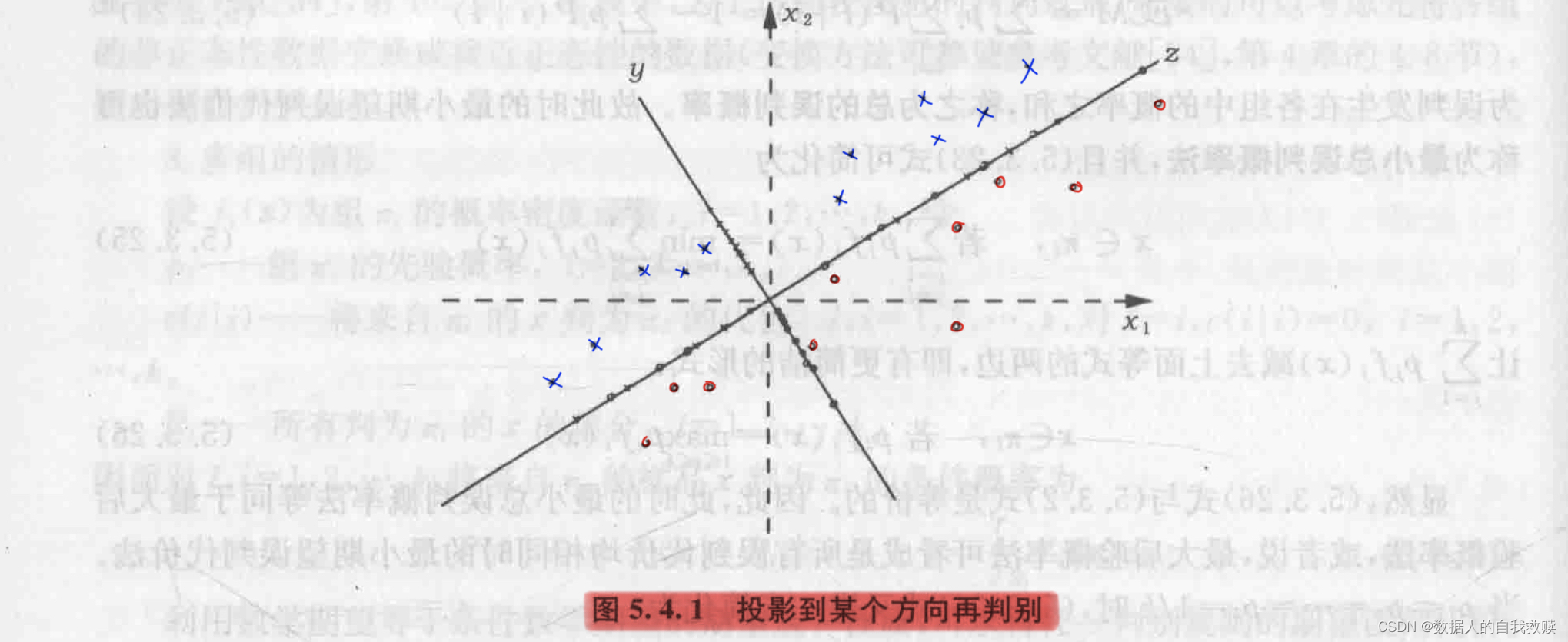
二、费希尔判别函数
1.函数寻找
设来自组的
维观测值为
,将他们共同投影到某一
维常数向量
上,得到的投影点可分别对应线性组合
费希尔判别需假定。
三组之间的分离程度:
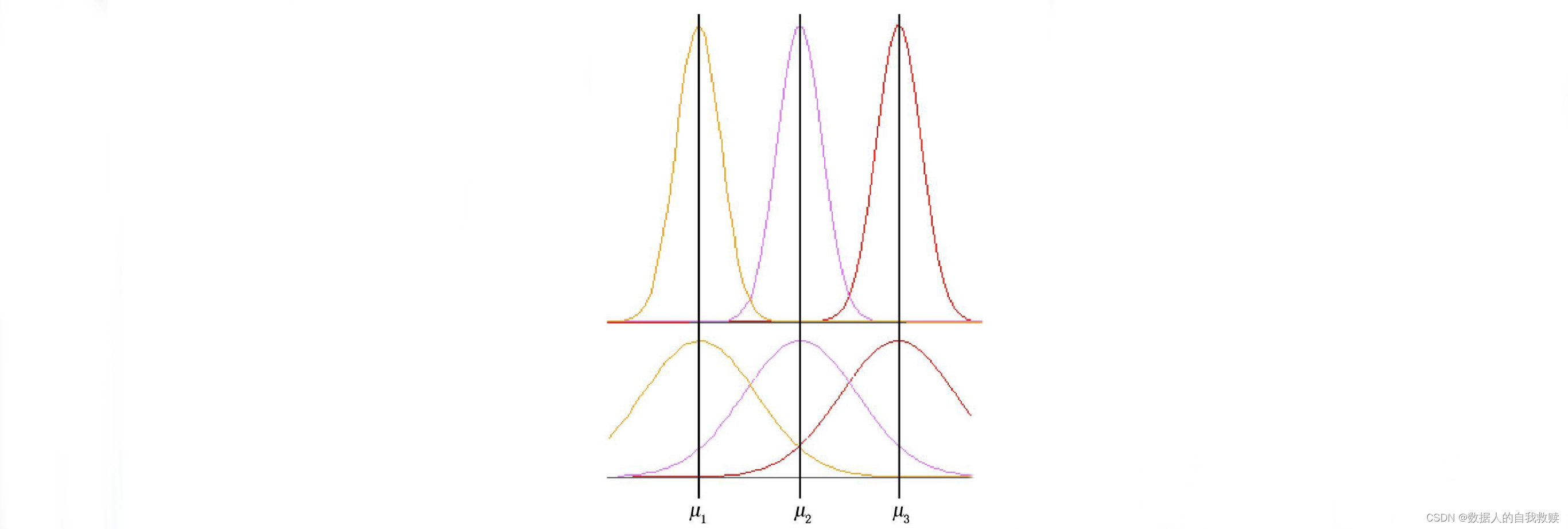
的组间平方和及组内平方和为:








 本文详细介绍了费希尔判别的基本思想、判别函数及其寻找方法,强调了降维在判别分析中的作用。通过实例展示了如何使用费希尔判别函数得分图进行直观的样本归属判断,并探讨了判别规则,特别是在两组情况下的应用。内容涵盖费希尔判别在数据分类和降维中的重要性及其局限性。
本文详细介绍了费希尔判别的基本思想、判别函数及其寻找方法,强调了降维在判别分析中的作用。通过实例展示了如何使用费希尔判别函数得分图进行直观的样本归属判断,并探讨了判别规则,特别是在两组情况下的应用。内容涵盖费希尔判别在数据分类和降维中的重要性及其局限性。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 6111
6111

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








