本部分的学习参考柯熙政老师的《无限光通信中的空间光——光纤耦合技术》及欧攀老师的《高等光学仿真(MATLAB版)》,为自学笔记,博客末尾附上了在学习过程中参考的博客内容。
承接上一章的内容,这一章基于对LP的理解进行补充和完善。
LP模的简并及其特征方程
通过上一章内容的学习,我们已经知道了LP模的简并度及其模式的特征方程:

注意:此处下标变为了lm,不再是之前内容中的mn。
时,光纤中只存TE模和TM模。当
时,出现的是
和
共存的EH模和HE模。为了区分,将特征方程右端取正号时对应的模式叫BH模,取负号对应的模式称HE模。
下面对它们的特征方程进行补充。上一章我们提到了:
在这章中,下标lm进行替换,可得:
由于,其中
为光波导的横向特征尺寸。则上式可以看成一个仅包含U或W的方程,。对于弱导光纤,认为纤芯与包层折射率极小
,可近似认为
。因此上式化简为:
这就是弱导光纤的近似特征方程。
TE_0m和TM_0m模
光纤中只存在的TE模和TM模。这是因为根据光纤矢量解表达式知,对于TE模,必有Ez=0,因此有常数A=0,代入式得
式中不能为零,相位常数
及常数B均不可能为零,因此只能使
。这样就得出结论,光纤中的TE模只能在
的情况下才能存在。同样,可以证明光纤中的TM模也只能在
的情况下才能存在。
在特征方程(3-1)中令,就可得到TE模和TM模的特征方程:
利用Bessel函数的递推公式
可把上式变换为
这就是TE模和TM模共同的特征方程。
EH模和HE模
当时,不能出现TE模和TM模,而只能是Ez和Hz同时存在,其中Ez所占的分量大时即为EH模(将特征方程右端取正号),反之为HE模(将特征方程右端取负号)。
因此,EH模的特征方程为
HE模的特征方程为
应用Bessel函数递推公式
简化后的特征方程为:
EH模:
HE模:
综上所述,在光纤中可存在4种类型的模式,分别为TE模、TM模、EH模、HE模。其中TE模、TM模只在时存在,而BH模、HE模在
时存在。各模式的特征方程可化为仅含一个未知量U(或W)的方程。在给定工作波长情况下,对应于一个L,Bessel函数就会有一系列解,求出的每一个U值的解就对应着一个模式。例如,对于EH模,对应一个l的Bessel函数第m个根所相应的U值解就代表了EH_lm模。因此,若光纤归一化频率V足够大时,光纤中可存在一系列的TE模、TM模和一系列的EH模、HE模。
LP模的截止条件
如前所述,LP_l,m 模是由弱导条件下简并模式HE_l+1,m模和EH_l-1,m模组合而成,它们的传播常数相同,特征方程等价。HE_l+1,m模和EH_l-1,m模的截止条件就是LP_lm模的截止条件。根据Bessel函数的渐进关系式,可以写出在
时,3种情况下LP_lm模的特征方程如下:

因此在模式截止时,上面3个方程的左边等于0,利用这一判据得到这3种LP模式的截止条件为:

LP模归一化截止频率的数值求解
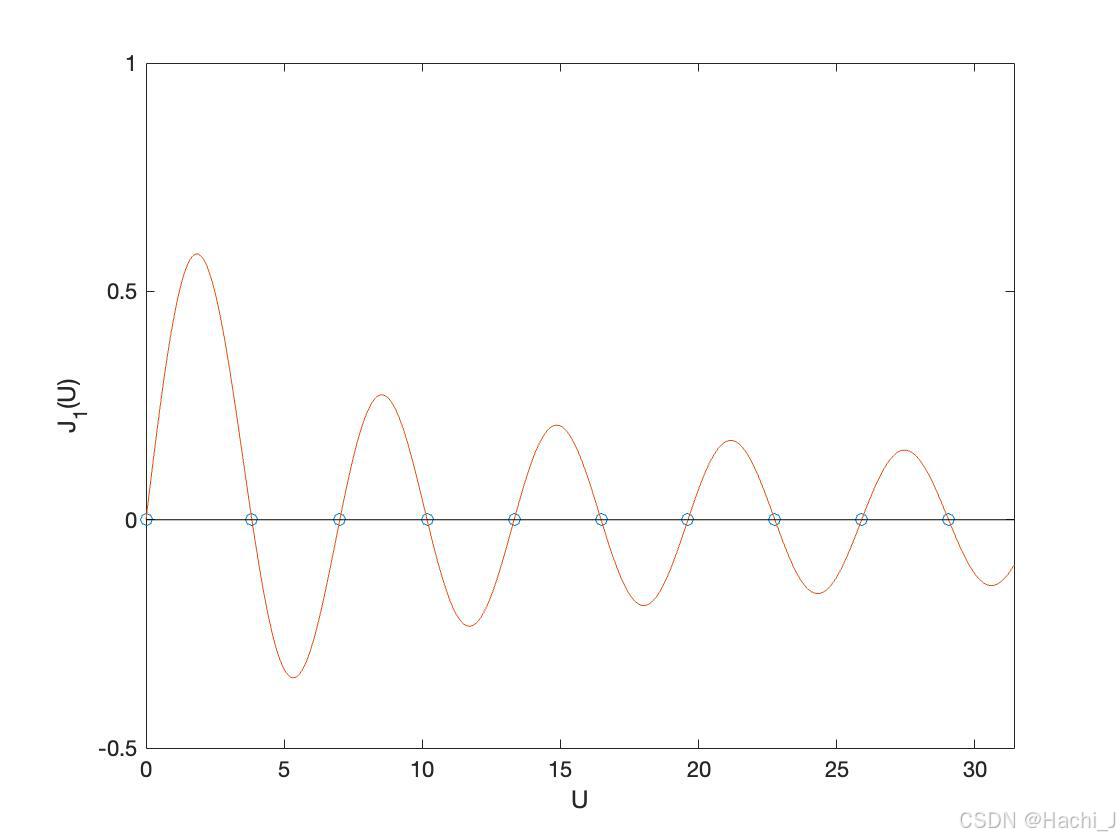
LP模归一化截止频率是指在光纤中,当某一LP模式的传输特性开始显著下降,即该模式即将无法再维持稳定传输时的归一化频率值。这个频率值标志着该模式在光纤中的有效传输范围。LP模归一化截止频率就是满足上述截止条件式的根,即不同阶数的Bessel函数的根。
Bessel函数的求解已在上一章给出,可以用matlab中的fzero()函数标注出根。
























 4370
4370

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








