梯度下降法法实现线性回归模型

晴天也会下雨吗

已于 2024-04-20 10:02:24 修改

阅读量1.2k

点赞数 30

文章标签：线性回归机器学习 python

于 2024-04-19 21:56:50 首次发布

本文链接：https://blog.csdn.net/m0_72600561/article/details/137978416

版权

一、线性回归模型

线性回归模型是一种预测性的建模技术，它研究的是因变量（目标）和自变量（特征）之间的关系。这种关系假设是线性的，意味着因变量可以通过一个或多个自变量的线性组合来预测。数学上，线性回归模型可以表示为：

$(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_nx_n)$

其中：

$(y)$ 是因变量（目标变量）。
$(x_1, x_2, \ldots, x_n)$ 是自变量（特征）。
$(\beta_0, \beta_1, \beta_2, \ldots, \beta_n)$ 是模型的参数，其中 $(\beta_0)$ 是截距， $(\beta_1, \beta_2, \ldots, \beta_n)$ 是各个特征的系数。

在机器学习和统计学中，线性回归模型通常通过最小化预测值和实际值之间的误差（例如均方误差）来估计这些参数。梯度下降法是一种常用的优化算法，用于找到最小化误差的参数值。

二、梯度下降法（Gradient Descent）

梯度下降法是一种优化算法，主要用于寻找函数的最小值。它的基本原理是通过不断迭代更新参数，从而逐步接近函数的最小值点。具体来说，梯度下降法通过在当前参数点处计算函数的梯度，并沿着梯度的反方向（即函数值下降最快的方向）进行参数更新，从而逐渐逼近函数的局部最小值。

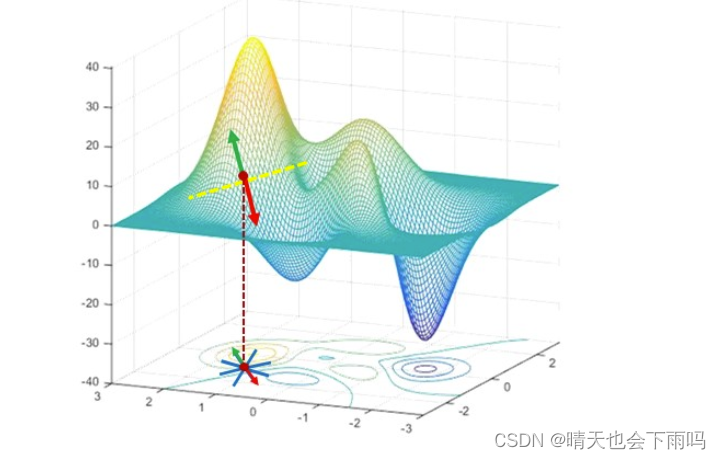
在使用梯度下降法时，通常需要初始化参数，并设定一个学习率来控制每次参数更新的步长。学习率的选择对算法的性能有很大影响，过小的学习率可能导致算法收敛速度过慢，而过大的学习率则可能导致算法在最小值附近震荡而无法收敛。

在MATLAB中，你可以使用内置的函数或手动实现梯度下降法来拟合线性回归模型。下面是一个使用MATLAB动实现梯度下降法进行一元线性回归的简单示例：

clear;clc;clf;

%导入x数据和y数据
x = [1,2,3,4,5,6,7,8,9];
y = [2.5,4.7,6.4,8.3,10.5,12.8,13.1,15.6,18];

%初始化参数
k = 0;%斜率
b = 0;%截距
learning_rate = 0.01;%学习率
precision = 1e-6;%精度
max_iter = 1000;%最大迭代次数

%预测值和均方误差
predict = @(k,b,x) k*x+b;
cost = @(k,b,x,y) sum((predict(k,b,x)-y).^2/length(y));

%梯度下降法
costs = zeros(max_iter,1);
for i = 1:max_iter
    %计算梯度
    grad_k = 2/length(y)*sum((predict(k,b,x)-y).*x);
    grad_b = 2/length(y)*sum(predict(k,b,x)-y);

    %检查梯度是否足够小
    if abs(grad_k)<precision && abs(grad_b)<precision
        fprintf('找到迭代%d次\n.',i);
        break;
    end

    % 更新参数
    k = k-learning_rate*grad_k;
    b = b-learning_rate*grad_b;

    %储存成本
    costs(i) = cost(k,b,x,y);

end

%输出结果
fprintf('Slop(k) = %f\n',k);
fprintf('Intercept (b) = %f\n',b);
%利用MATLAB自带拟合函数对比
p = polyfit(x,y,1);
fprintf('k = %f\n',p(1));
fprintf('b = %f\n',p(2));
figure(1);
plot(costs,'LineWidth',2.5);
xlabel('迭代次数');
ylabel('均方误差');

%可视化
figure(2)
scatter(x,y);
hold on
plot(x,predict(k,b,x),'r-');
xlabel('x');  
ylabel('y');  
axis([0,9,0,18]);
legend('Data points', 'Fitted line');  
hold off;

均方误差随迭代次数的变化如下图：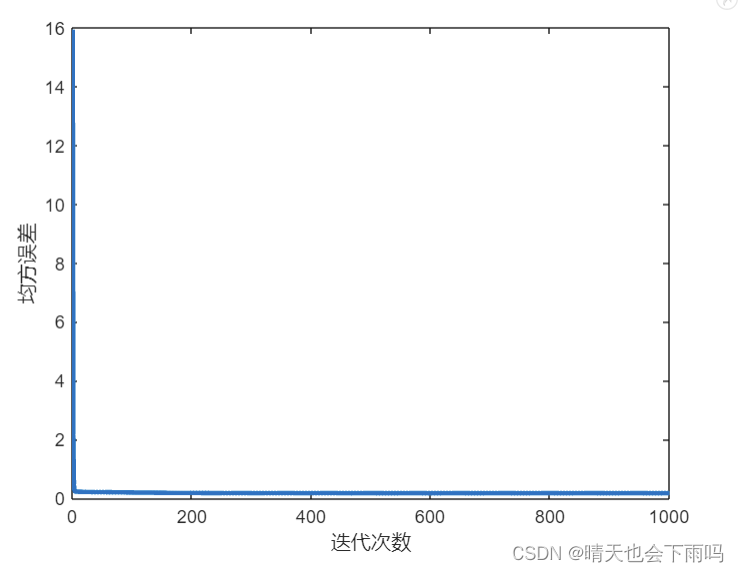

初始数据点和梯度下降法求解出的的曲线如下图：

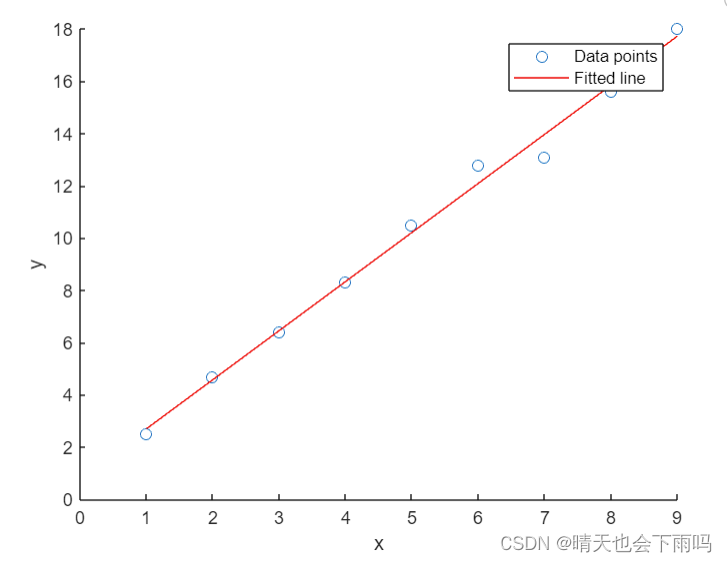
三、线性回归模型的优缺点

优点：

解释性强：线性回归模型具有很好的解释性，因为每个特征都有一个对应的系数，这些系数可以直观地表示该特征对目标变量的影响程度。这使得模型的结果易于理解和解释。
计算简单：线性回归模型的计算相对简单，无论是模型的训练还是预测，都可以通过矩阵运算高效地实现。这使得线性回归在处理大规模数据集时具有较好的性能。

缺点：

假设性强：线性回归模型假设自变量和因变量之间存在线性关系，这在实际问题中可能并不总是成立。如果数据中的关系是非线性的，那么线性回归模型的预测性能可能会受到影响。
对异常值敏感：线性回归模型对异常值（或称离群点）比较敏感。异常值可能会对模型的参数估计产生较大的影响，导致模型的预测性能下降。因此，在使用线性回归模型之前，通常需要对数据进行清洗和预处理，以消除或减小异常值的影响。
特征相关性问题：当自变量之间存在高度相关性时（即多重共线性），线性回归模型的参数估计可能会变得不稳定，导致模型的预测性能下降。此外，多重共线性还可能使得模型的解释变得困难。

综上所述，线性回归模型具有解释性强、计算简单等优点，但也存在假设性强、对异常值敏感等缺点。因此，在选择是否使用线性回归模型时，需要根据实际问题的特点和需求进行权衡和考虑。