“深度学习”学习日记。神经网络的学习--数值微分、梯度法

在撒哈拉卖雨伞

于 2023-01-09 19:28:55 发布

阅读量218

点赞数 1

文章标签：深度学习神经网络学习

本文链接：https://blog.csdn.net/m0_72675651/article/details/128614982

版权

2023.1.9

之前学习损失函数的时候，提到了之后会学习到函数的梯度法，而今天就是这个内容的学习。

导数：

在学习之前我们需要回忆一下导数和极限的概念，这个概念对于学过高中数学和高等数学的人并不陌生：

$\frac{df(x)}{dx}=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

像现在这样我们所求得到的导数是“假的导数”，“真的导数”对应于x处的切线（斜率），这个误差的原因当然是因为h不能趋近于0。

像这样用微小的差分求导数的过程就称为数值微分

而基于数学推导式推导的导数称为解析性求解

import numpy as np
import matplotlib.pyplot as plt

# def numercial_diff(f, x):
#    h = 10e-50
#    return (f(x + h) - f(x)) / h

print(np.float32(10e-50))  # 0.0 如果用32位数的浮点数来表示则无法正确表达
print(np.float64(10e-50))  # 1e-49

为了减少误差，我们可以利用 $f(x+h)-f(x-h)$ 之间的差分，这样以x为中心差分也称为中心差分，而 $f(x+h)$ 称为前向差分。

import numpy as np
import matplotlib.pyplot as plt


# def numercial_diff(f, x):
#    h = 10e-50
#    return (f(x + h) - f(x)) / h

def numerical(f, x):
    h = 1e-8
    return (f(x + h) - f(x - h)) / (2 * h)


def f(x):
    return np.log(x)


x = np.arange(0.1, 10.0, 0.1)
y = f(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y, label="log(x)")
plt.title("log(x)")
plt.show()

print(numerical(f, 5))  # 0.20000000544584395
print(numerical(f, 10))  # 0.1000000082740371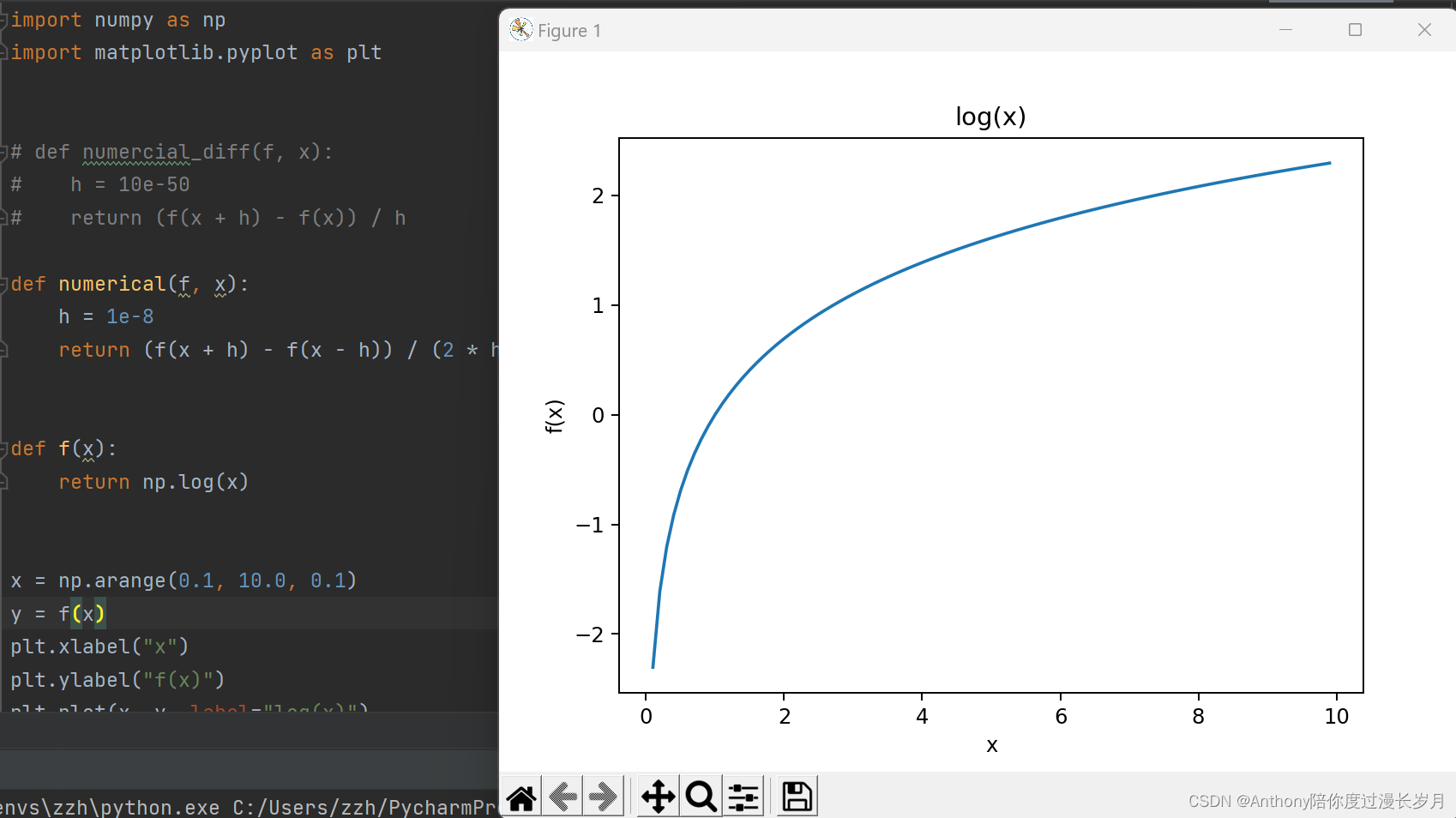

偏导数：

这东西学过高等数学的都明白，抓住主题言归正传，就不赘述了吧，直接上代码

假设一个函数：

$f(x_{0},x_{1})=x_{0}^{2}+x_{1}^{3}+9$

对 $x_{0}$ 的偏导数： $\frac{\partial f}{\partial x_{0}}=2x_{0}$ ; 对 $x_{1}$ 的偏导数： $\frac{\partial f}{\partial x_{1}}=3x_{1}^{2}$

# 利用数值微分
#
def numerical(f, x):
    h = 1e-8
    return (f(x + h) - f(x - h)) / (2 * h)


def f_x0(x0):
    return x0 * x0


def f_x1(x1):
    return x1 ** 3


while True:
    print("输入x0的值")
    x0 = float(input())  # 2
    print("输入x1的值")
    x1 = float(input())  # 2
    print("x0的偏导数")
    print(numerical(f_x0, x0))  # 3.999999975690116
    print("x1的偏导数")
    print(numerical(f_x1, x1), '\n')  # 11.999999882661427

梯度：

概念也不多说，刚才实现了偏导数的计算，现在我们来看看 $(x_{0},x_{1})$ 偏导数 $(\frac{\partial f}{\partial x_{0}},\frac{\partial f}{\partial x_{1}})$ ;即梯度。

严格地讲，梯度指示的方向是个点函数值减少最多的方向。

在高等数学理我们也学习过，方向导数 = cos（θ）× 梯度 ，因此，梯度的方向是下降速度最快的方向

import numpy as np


# 利用数值微分
#
def numerical(f, x):
    h = 1e-8
    return (f(x + h) - f(x - h)) / (2 * h)


def f_x0(x0):
    return x0 * x0


def f_x1(x1):
    return x1 ** 3


while True:
    print("输入x0的值")
    x0 = float(input())  # 2
    print("输入x1的值")
    x1 = float(input())  # 2
    c1 = numerical(f_x0, x0)
    c2 = numerical(f_x1, x1)
    print("(x0,x1)的梯度：")
    print(np.array([c1, c2]), '\n')

梯度法：

在神经网络的学习过程中，就是在利用损失函数的值作为反馈情况来调整参数，从而寻找最佳的参数去优化模型，这里讲的最佳参数就是指使损失函数最小值是的参数。由于损失函数很复杂，参数范畴很大，我们这是就可以利用“梯度”来寻找损失函数的最小值的“方向”，这样的方法也称为 梯度法 。

高等数学中学过，函数的极小值、最小值以及被称为鞍点的地方，梯度为 0 。鞍点从一个方向上看是函数极大值，另一个方向是函数的极小值。当函数复杂且呈现扁平状时，神经网络的学习也可能会进入一个平坦的区域（梯度处处为0），陷入停滞状态，这称为 “学习高原” 。

如图马鞍面函数：

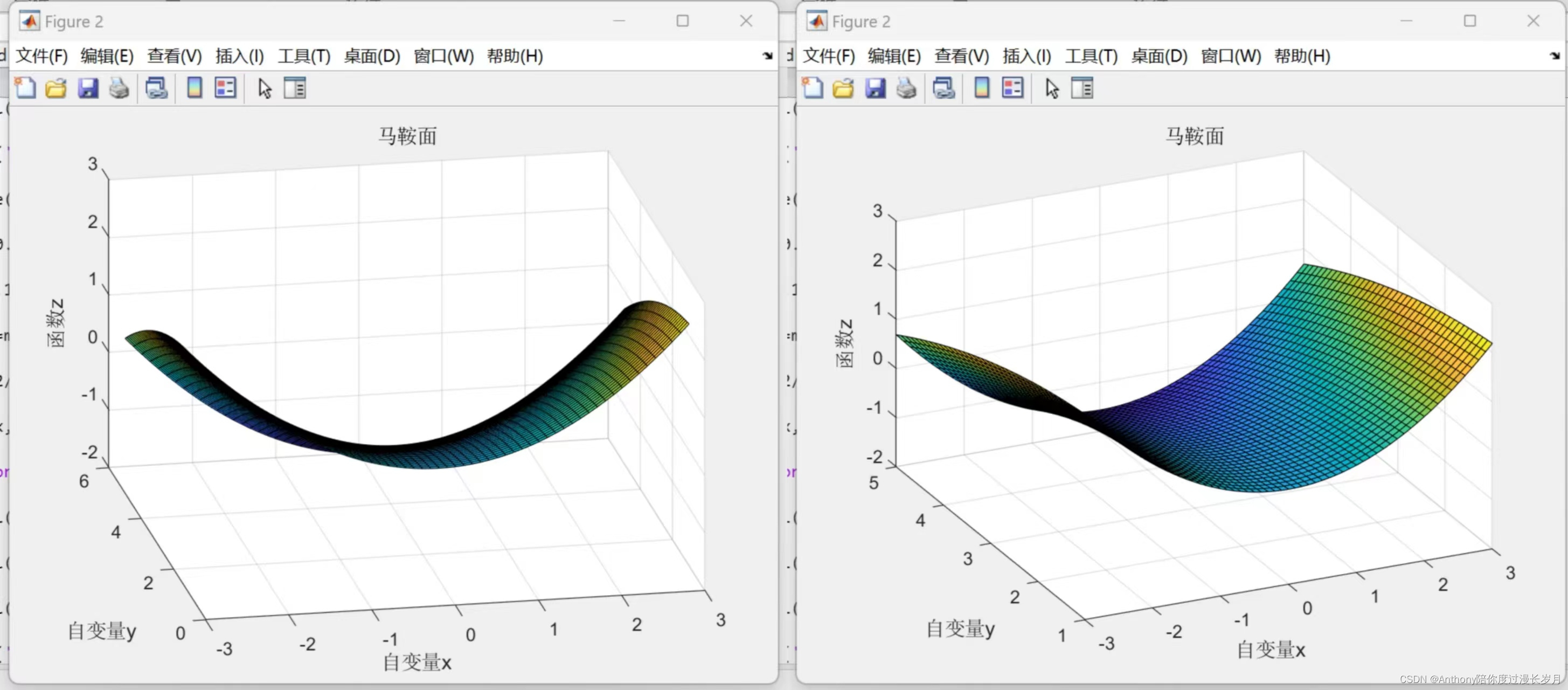
梯度的方向不一定指梯度指向下降的方向，根据目的寻找最大值还是最小值，梯度法的叫法不同，寻找最大值的梯度法称为 梯度上升法 ，寻找最小值的梯度法叫做 梯度下降法 ；一般而言，在神经网络的学习中，梯度法主要是梯度下降法。对面复杂的函数我们需要沿着梯度方向前进一段距离以后，然后再新的位置再求梯度，反复进行。而这样重复的更新参数，我们称之为 学习率

卷不动了，今天就先学到这里吧 19.28