管道应力理论（应用）

        本文仅对管道应力涉及的理论知识（偏向于应用）进行简单介绍。

        管道应力：对管道应力校核是为了防止管壁内应力过大对管道造成破坏，不同的荷载引起不同类型的应力，在实际工程应用中，一般分为三种：一次应力、二次应力、偶然应力，主要对管道轴向应力进行校核。

1 一次应力

1.1 公式

        一次应力σi为持续应力（SUSTAIN STRESS）：为平衡内压、重力、其他外力荷载（持续性荷载）的作用产生的应力；

        (非完全约束管道)[σ]L=(PD/4t)+(iM/Z)+F/A≤[σ]h

        [σ]L ——（longitudinal）轴（纵）向应力，MPa；

        F  ——其他外力（轴向力），如摩擦力、盲板力，N；

        A  ——管道截面积，mm²；

        P  ——设计压力，MPa；

        t   ——管道壁厚，mm；

        i   ——（弯头、三通、大小头）应力增大系数；

        M ——管道自重产生的合成弯矩，N·mm，管道可视为简支梁与固支梁之间的情况模型，最大弯矩：M=wL²/10，其中w为均布型载荷，L为简支梁长度，10为经验数据；

        Z  ——抗弯截面模量，mm³，Z=π(D^4-d^4)/64,D为外径，d为内径。

        公式中，内压荷载应力可以更精确：Pd²/(D²-d²)，

        D  ——管道外径，mm；

        d  ——管道内径，mm；

        [σ]h——热态许用应力，MPa。

1.2 特点

1.2.1 没有自限性

        当管道内的塑性区扩展达到极限状态，使之变成几何可变的机构时，即使外力荷载不再增加，管道仍将产生不可限制的塑性变化，直至破坏（材料力学——拉压试验）。

        

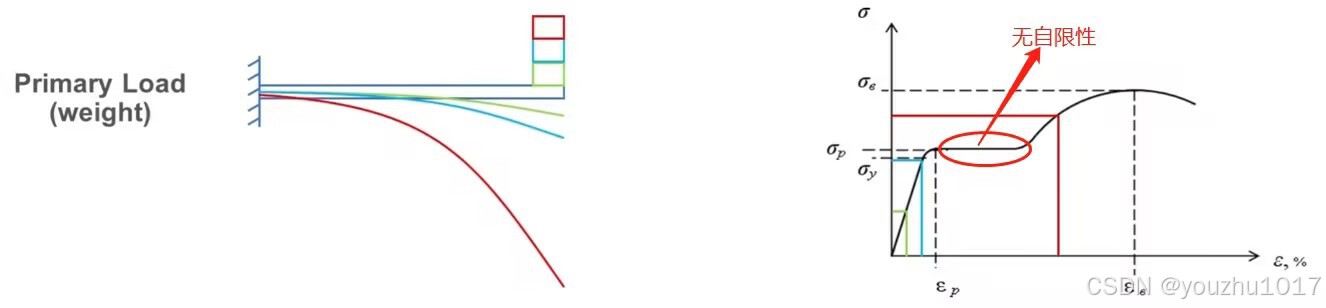
1.2.2 塑性变形不可恢复性

        在断裂极限和屈服极限之间的管道，当外力荷载将为0时，管道应变不会恢复到0点，会留下残留变形，下图中OY段即是应变残留。

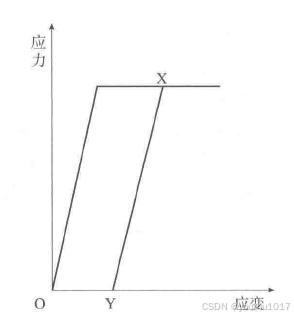
1.2.3 管道跨距

        由上述公式可知，影响一次应力主要是管道壁厚t和管道长度L，又因为管道壁厚通常情况下由材料专业已经明确，所以一次应力的调整主要取决于管道跨距：

L=√{(Sh-PD/4t)-(10Z/iw)}

        

2 二次应力

2.1 公式

        二次应力σii为热胀应力（EXPANSION STRESS）：因热胀、冷缩、端点位移等位移荷载的作用产生的应力；

        因管道膨胀的情况多，计算复杂，这里为解释原理，只简单介绍L型管道模型：

 

Se=i3EDΔ/L²≤σii，

F=E A a ΔT，

        Se ——热应力，MPa；

        i  ——（弯头、三通、大小头）应力增大系数；

        E ——管材的弹性模量，MPa；

        D ——管道外径，mm；

        Δ  ——管道的热膨胀量，mm;

        L  ——管道臂长（与膨胀方向垂直管道，图中F方向），mm；

        σii——许用应力（取值见2.3条），MPa

        F  ——推力，N；

        A  ——管道截面积，mm²；

        a  ——管材线胀系数，1/℃；

        ΔT ——温差，℃。

        
        由上述公式可知，管道臂长可以调节二次应力。

2.2 特点

2.2.1 有自限性        

        当局部屈服和产生少量塑性变形时，管道通过变形协调就能使应力降低下来。

2.2.2 安定性

        当（热胀）载荷在一定范围内（弹性应力小于2倍屈服极限σs）反复变化时，结构内不发生连续的塑性变形循环。即图中：O→A→B→D→B→D......该结构便达到安定。

         当载荷超过2倍屈服极限时，即图中O→A→B‘→D→E→B→B''→F→D→B'......该结构每次在膨胀到收缩的循环中，便发生一次正向和反向的塑性变形，最终导致管道金属疲劳、破坏。

 

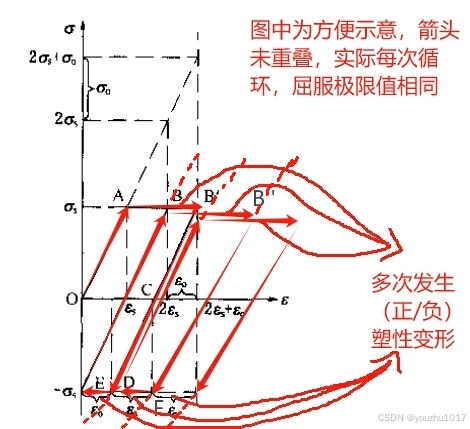
        所以， 对于压力管道（往复式压缩机管道除外）二次应力来说，主要是为了避免出现上述这种反复的循环塑性变形，防止低疲劳破坏（低周疲劳破坏：应力水平较高时，材料在应力循环次数低于1万次就发生破坏）。

2.3 许用应力σii

        考虑到膨胀/收缩循环过程中，管道可能处于冷态[σ]c和热态[σ]h两种状态，为兼顾冷、热态且留出安全裕量（“1.25”），最后加上“一次应力σi≤[σ]h”的条件，二次应力σii的许用应力取：

                                                              σii≤ 𝑓×{1.25×[σ]c+0.25×[σ]h)}，

       𝑓为应力范围减小系数，如果热胀/冷缩载荷循环次数≤7千次，该值取1；超过7前次，该值便逐级变小，以减小许用应力。

        该值是防止发生高周疲劳破坏（应力水平较时，材料无明显塑性变形，材料在应力循环次数高于1万次发生破坏，常见于转动机器和往复式压缩机管道）。

 

3 偶然应力

         偶然应力（OCCASIONAL STRESS），在实际项目中，常见的偶然载荷有：风载荷、雪载荷、地震载荷、运输载荷。

3.1 公式

        因为偶然载荷会使管道产生弯曲，所以

σocc=M/Z≤k[σ]h-σi

        M ——偶然载荷产生的合成弯矩，N·mm；

        Z  ——抗弯截面模量，mm³，Z=π(D^4-d^4)/64,D为外径，d为内径；

        k ——偶然载荷常数，不同行业管道取值不同，工艺管道取1.33，动力管道取1.2；

        [σ]h——热态许用应力，MPa；

        σi——一次应力，MPa。