目录
一.不同进制之间的转化
这个其实我们已经很熟悉了,我们接下来看一下这幅图,了解具体不同进制间是如何转化的.
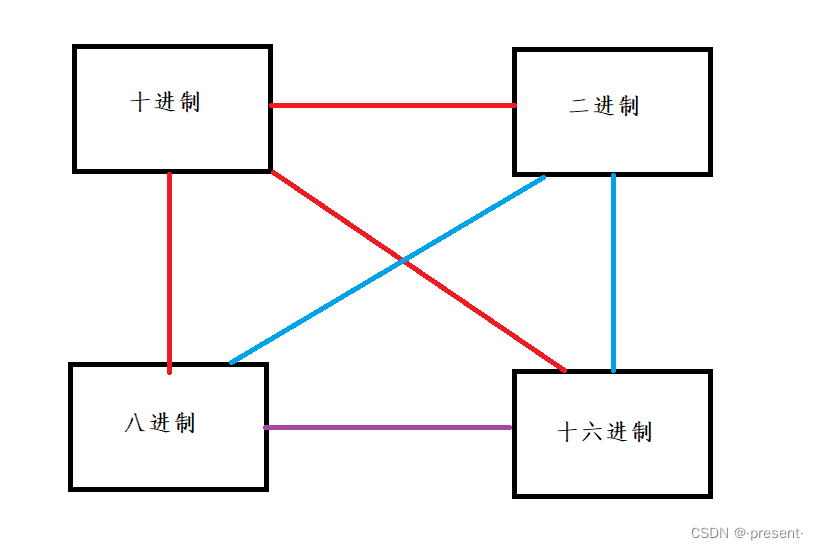
1.十进制和不同进制之间的转化方法
首先,我们看红色这三条线,是十进制和不同进制之间的转化方法.
在这之前,我们必须先了解一个叫做位数和权的概念.
123.5这个十进制数,实际上可以分解为1 * 10^2 + 2 * 10^1 + 3 * 10^0 + 5 * 10^(-1),而2,1,0,-1这些数就是位数(也称为权系数),10^2就是1这个数的权,10^1就是2这个数的权...
也就是每位数虽然看上去都是0-9的取值,但它们的地位(权)可不同,或者说占的分量不同,1作为最高位对应的权重会更高.
 比方说1101这个二进制数,转化为十进制数,也是如此,从右往左,位数依次增大
比方说1101这个二进制数,转化为十进制数,也是如此,从右往左,位数依次增大
1 * 2^0 + 0 * 2 ^1 + 1 * 2^2 + 1 * 2^3 ,计算得到13,13便是1101这个二进制数转化为十进制数的结果.
再比如说2A.7F这个十六进制数,
2 * 16^1 + A(10)* 16^0 + 7* 16^(-1) + F(15) *16^(-2),计算得到42.49609375,便是2A.7F这个十六进制数转化为十进制数的结果.
至此,我们便可以类比,学会将所有进制数,转化为十进制数的方法.
总结:每一位数值乘以对应权重相加,即可任意数制转化为十进制.
那我们就要问,如何将十进制转为其它进制呢?
一般我们会将一个数分为两个部分进行处理,一个是整数部分,另一个则是小数部分,因为两个部分处理的方法是有差异的,前者是不断相除,从下往上取余数,后者则是不断相乘,从下往上取整数.
我们接下来举一个具体的例子,比如173.8125这个十进制数,我们想把它化为二进制数.
它的整数部分是173,小数部分是0.8125
对于整数部分173,我们就不断除以2,直到碰到被除数为1停止,然后从下往上取余数.

最后,173便化为10101101这样一个二进制数 .
进一步思考,这个方法到底是怎么来的呢?
其实非常简单,我们前面提到过任何一个数都可以权系数与权相乘求和的形式
比如说任意一个十进制数字,其实可以表示为二进制权系数与权相乘求和的多项式形式,R为基数(radix,假如是上述例子的十进制转为二进制,则R = 2),b就是我们的权系数
我们的任务就是要求解对应的权系数而已!
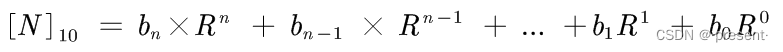
不断除以对应的基数R = 2,假如第一次除,得到的会是下面这个表达式
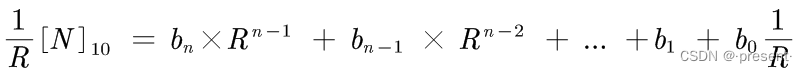
那什么是取余数操作呢?
就是把前面红色划线的整数部分不要,剩下绿色划线小数部分数字仍然保留,此时我们就取出来了对应转化后的二进制数字的最后一位!

以此类推,将红色的整数部分重新作为新的数字,继续进行上述操作,直到数字不能再除为止.
由于每一次数字取的都是最后一位,因此要从下往上读
同理,小数部分也是同样的操作,只不过对应的权系数有所不同
![]()
我们的目标同样是求解对应二进制表达式中的权系数
假如除以对应的基数R,再进行取余,是得不到任何我们想要的值的,没有一个R被消去
正确的做法应该是乘以对应的基数

通过乘基数的操作,我们就拿到了b-1这个权系数(整数)
以此类推,直到b-n被求解出来
由于每次取出来的是最靠近小数点的数字,所以由上往下读
比如对于小数部分0.8125,我们就不断乘2,直到乘到1为止,然后从上往下取整数排列.
PS:
1.值得注意,每次乘2后,所得的数,整数部分如果大于1,就要相应取出来,下次相乘就不再出现,比如下图第一次相乘得到的1.625,那第二次相乘是用0.625乘2,而不是1.625.
2.有时候一直得不到1,所以有部分十进制数未必能完全转化二进制数,只能不断逼近,这也导致计算机中C语言存储浮点数,未必精确,进而浮点数不能比较大小.
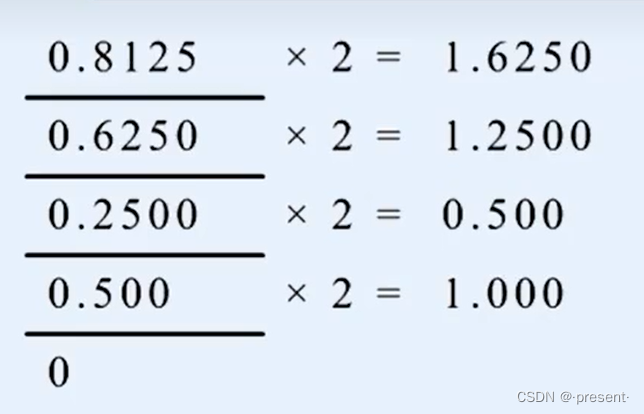
最后,0.8125便化为1101这样一个二进制数
于是,把两者结合起来,便可以得到10101101.1101这样一个二进制数,这就是173.8125转化得到的二进制数.
我们还可以直观理解这两个操作,它有点类似我们其它进制数得到十进制数的逆过程,173的每次相除,得到的余数,会随着相除次数增加,而对应位数增加,有种层层筛选的感觉,同理,0.8125也是如此.
总结:
整数部分,不断除2,从下往上取余数.(除基取余法)
小数部分,不断乘2,从上往下取整数.(乘基取整法)
PS:十进制转十六进制,八进制,也是类似操作.
2.二进制和八进制的不同转化方法
接下来,我们看下蓝色的三条线间的关系.
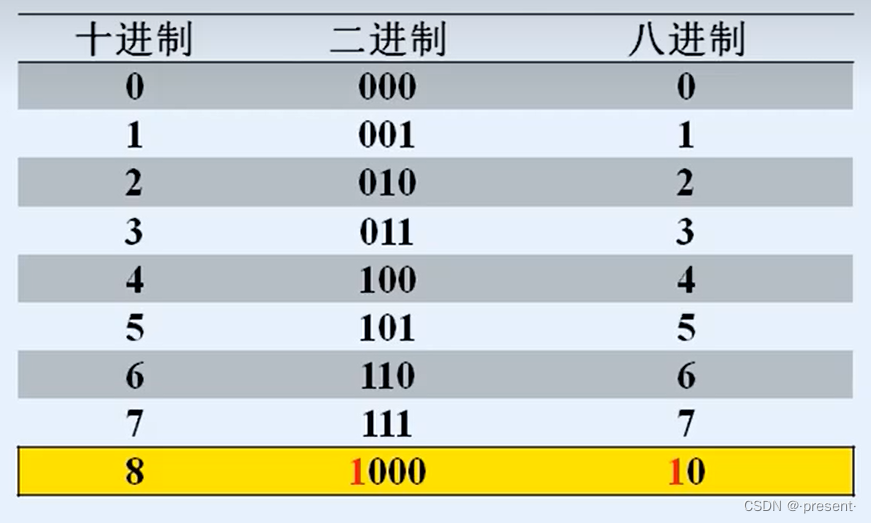
对于11这个八进制数,对应十进制的9,二进制为1001,我们会惊奇地发现,三位二进制数恰好能够和八进制数一一对应,并且还会出现八进制进位,对应二进制也循环的现象,因此,我们就得到下面转化的方法.
从右往左,将3位二进制数看成一个整体,不足3位补0,等价为1个八进制数.
例如:1001看作001 001,刚好就对应八进制11,再比如1101,看作001 101,刚好也对应八进制15
反过来,把八进制转为二进制数,就是把每个数,对应化为二进制数即可.
比如52.43这个八进制数,先将每一位化为二进制数,然后再合起来,便得到101010.100011对应的二进制数了.

3.二进制和十六进制的不同转化方法
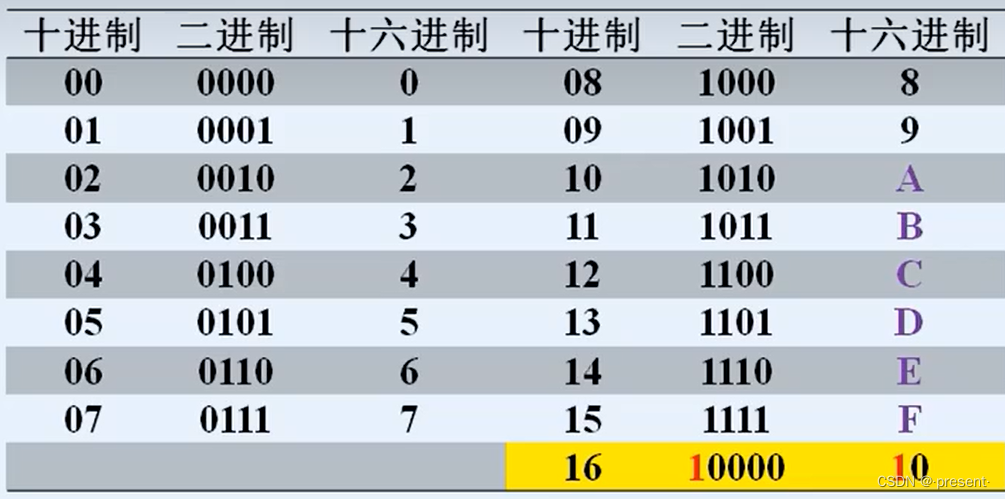
和八进制类似,4位二进制数也能够不重复和十六进制每个数一一对应,并且在十六进制进位时,二进制也恰好出现循环现象(10000中的0000) .
因此,我们可以得到如下转化方法
整数部分从右往左(小数部分从左往右)将4位二进制数看成一个整体,不足4位补0,等价为1个
十六进制数.
例如:
1011110.1011001这个二进制数,我们要把它转为十六进制数,将4位二进制数看成一个整体替换,不足就补0

十六进制转为二进制也类似八进制转为二进制,将每一位化成4位二进制即可,这里不再过多介绍.
4.十六进制和八进制的转化
没有特殊方法,将二进制作为桥梁,先转成二进制,再进一步转化为目标进制即可.
有关原码,反码,补码的介绍,可以看我之前写的C语言数据存储的文章,这里不再重复介绍
https://blog.csdn.net/m0_72873854/article/details/126441390
二.二进制常用的编码形式
1.8421BCD码(恒权码)
BCD码即二-十进制代码,是用四位二进制数代码表示一位十进制数码.
它是一种有权码,也可被称为恒权码,从左往右的权值依次为8 4 2 1

类似的恒权码还有2421码,5421码等等,顾名思义,就是权重分别为2 4 2 1和5 4 2 1的说法.

理解上述的编码形式其实不难,就是不同位权值不同而已.
但是我们需要思考的是,为什么会出现这么多不同形式的编码?我用二进制与十进制直接一一对应不就好了?
第一,我们还是拿8421码来举例,十进制数从0-9,总共十个数字;8421码,假如全部使用,总共可以表示16个数字,这就意味着可操作的空间很多,我们也可以用1111来对应9的编码,而不一定要用1001,编码的方式不唯一(可操作性强)是形式丰富的前提
第二,假如用8421码来计算9+2,得到的将会是1001 + 0010 = 1011,而1011显然不落在我们的8421编码之中,11没有对应的编码;
但是我们采用无权的余3码(比8421码多3)进行编码呢?我们惊奇的可以发现,任意两个余3码表示的十进制数相加时,能正确产生进位信号,比如5(1000) + 6(1001)会产生1的进位.当然“和”还必须进行修正,否则加出来的结果是错的.
修正的方法是:如果有进位,则结果加3;如果无进位,则结果减3
5(1000) + 6(1001),有1的进位,所以结果要加3,0001 + 0011 = 0100,对应余3码的1,即最后的运算结果为11
因此,出现这么多不同形式编码,是因为我们需要解决不同场景下的应用问题,没有一个编码方式可以说是完美的,都需要付出不同的代价才能换取对应的性能.
2.格雷码 (循环码)
格雷码一个特征就是,相邻两个码之间只有一位不同,每一位的状态都按一定顺序循环.

像上图列举的四位格雷码,每次变化,都只有1位二进制位变化,像0111和0101,就只有一个1发生变化,同样值得注意,1000和0000依旧也只有1位变化,是一个闭环的处理.
格雷码的优势在于哪呢?
由于相邻代码只有一位发生变化,在代码过程转化过程中,不会出现过度“噪声”.
这是什么意思呢?举一个简单的例子,假设现在5要往6发生转变.

按照原来二进制码进行转化的话,理想情况,我们当然希望不同的两位会同时发生变化,但我们知道会有延迟,所以会导致出现两种情况
我可以先把0101,变成0111,再变成0110 ;
也可以先把0101,变成0100,再变成0110
而0111和0100是我们不希望要的信号,这就是过渡过程中的"噪声".
但格雷码就不会出现这种情况,每次都是直接一步完成.
这个问题并非特例,实际上数字电路中,比如计数器各位输出不是同时进行变化,是很正常的现象,此时就会造成严重错误.
那我们要怎么编写格雷码呢?
这里实际上是有规律的,我们先要把一组数0 1 1 0记在心中,最低位,一定是不断循环这四个数的
随后,每一个下一位新的数,都是上一个新的位上的数,循环出现两次.
这里我们写一个三位格雷码来加深理解这个过程.
首先,3位格雷码,2*2*2=8,必定有8个格雷码,我们先把最低位写出来.

那对于第二位,就是第一位的数,重复两次出现.0重复出现2次,接着是1出现2次,再接着是1出现2次,紧接着是0出现2次,刚好是8位,便不再循环.
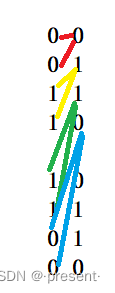
对于第三位,也是类似的操作.第二位的0重复出现2次,接着是0出现2次,再接着是0出现2次,紧接着还是0出现2次,刚好8位,不再循环.

于是我们便得到3位的格雷码,如图所示,检查可以发现,完全符合格雷码的特点要求

3.Ascll码
即美国信息标准交换码,由一组7位二进制代码组成,共128个.
它是一种国际通用标准代码,广泛应用于计算机和通信领域.
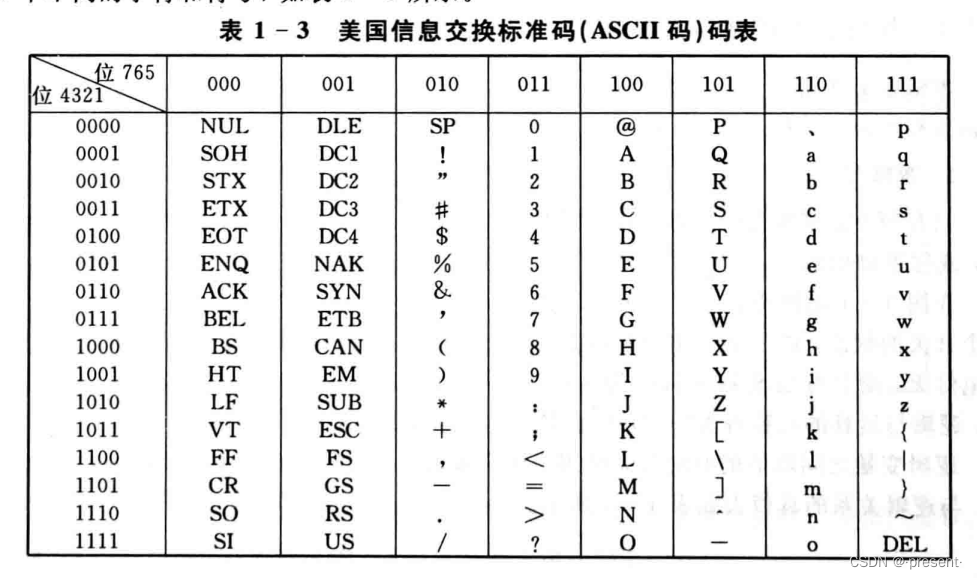
这里也不再过多解释,每个符号对应相应的二进制码,需要的时候,直接查表就可以.
三.逻辑代数的基本运算
逻辑这个词语所对应的含义是事物的因果关系
比如我们说一个人说话没有逻辑,牛头不对马嘴,就是指他前一句话和后句话一点关系都没有,在那胡说八道
事件是复杂多样的,但事件内容不是我们关注的重点,我们关注的是事件之间的因果性
那应该如何研究呢?
此时还是木匠的布尔提出了布尔代数的概念,将事情用0和1来进行抽象
我们也把这种,只有两种不同取值的变量,称为逻辑变量.
比方说
事件A:吃了K药,我们可以用1来表示,没有吃K药,用0来表示;
事件B:吃了J药,我们可以用1来表示,没有吃J药,用0来表示;
事件C:康复用1来表示,没有康复用0表示
现在已知只有同时吃了A药和吃了B药,才能康复,那我们就可以用数学的方式来描述事件之间的关联
只有A = 1且B = 1,才有C = 1
通过这样一种抽象的方式,将事物之间的关系用数学方式来进行描述,能够大大提高研究的效率(注重关系而不是内容),且精准
我们把对其中的逻辑状态(关系)进行推理运算,称为逻辑运算;
我们把研究逻辑运算的数学方法,被称为逻辑代数.

不过,这个时候,逻辑代数和我们的数字电路还没有任何关系
直到后面,我们大名鼎鼎的香农科学家,才将两者联系起来

香农发现,在数字世界之中,我们也是只有0和1,开关的闭合也是用0和1来构成
换言之,我们完全可以用逻辑代数去研究我们的数字电路
我们不关心开关闭合与否,即0和1是怎么产生的,它的实现方式不一定是半导体器件,未来可能有新的器件诞生,比如量子器件,但是逻辑代数依旧不会发生改变,它是一种比数字电路更抽象的方式
基本运算分为三类:与(AND),或(OR),非(NOT)
假如我们用1表示开关接通,小灯泡发光;0表示开关断开,小灯泡熄灭
基本运算对应的电路图就如下所示:.
1.与运算
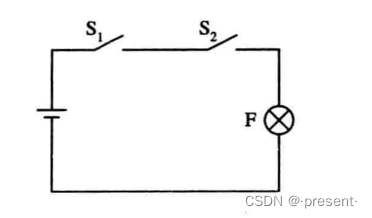

只有S1,S2同时接通,即都为1,才为1(小灯泡发光),其余都为0.
表示为F = S1 * S2 = S1S2.
2.或运算
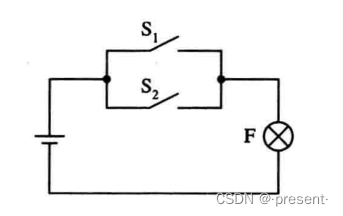
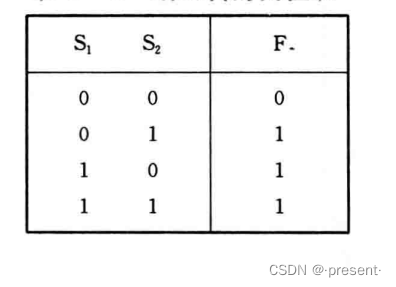
只要S1,S2有一个接通,即有一个为1,就为1(小灯泡发光)
只有S1,S2全部没有接通(都为0),才为0(小灯泡熄灭)
表示为F = S1 + S2.
3.非运算


开关闭合(1),灯泡必灭(0),反之,开关断开(0),灯泡发光(1).
表示为F =
4.其它常见逻辑运算
异或运算 相同为0,相异为1
1.两个相同的信号异或,得0
2.与0做异或运算得原变量,与1做异或运算得反

进一步思考,异或表达式是如何用与或非表达的呢?
研究一个问题,首先是要把问题描述清楚
什么是异或运算呢?看真值表来说
当A = 1且B = 0时,或者,A = 1且B = 0时,有输出1,除此之外输出都为0
且——代表的不就是我们的与运算吗?
或——代表的不就是我们的或运算吗?
A和B不同——A和B其中有一个取反
于是便得到我们的异或表达式如下:
![]()
同或运算(异或运算的非运算)
相同为1,相异为0
![]()

与非运算(先与后非)
F =
只有全为1,才为0,其余全为1

或非运算(先或后非)
F =
只要有1,必为0,只有全为0,才为1.

还有比如与非与非,和或非或非,这里不细谈

5.门电路
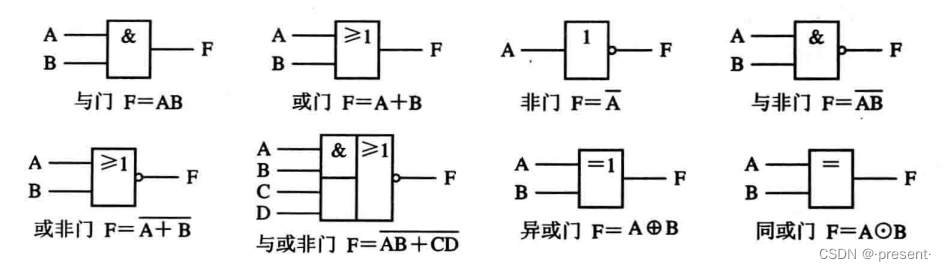
当然,现在更多用得是下面这种形式
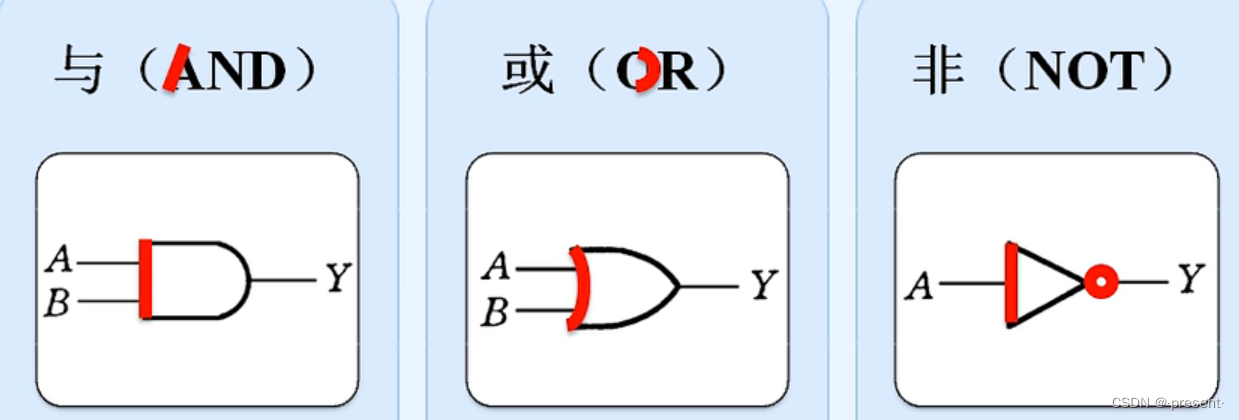
记忆方式也如上图所示,AND中的A是竖,因此图片左端为一竖线,OR中的O是弯,因此图片左端为一曲线,非则和上图类似,也是图片右端有个小圆圈.
四.逻辑代数的基本公式与常用公式
为了加深对公式的理解,我们用数学中的集合概念进行类比记忆.
1就代表全集,0就代表空集,逻辑与对应交集,逻辑或对应并集,逻辑非对应取补集
1.常量公式

2.变量公式
 这里举A
这里举A = 0来说明
A只能取0或者1,无论A取什么值,A和 必然不相等,而逻辑与只有全为1,才为1,所以得到的必为0.
从集合角度也很好理解,A和A的补集,两者的交集,必定为空集.
不要觉得它简单,有一些公式其实挺违背我们的直觉认识的
比如说A·A = A,而不是等于A^2,从右往左看,我们可以把A逻辑变量,拆成两个相同逻辑变量相与的形式(A集合与自身的交集,还是它本身)
再比如说A + 1 = 1, = 1,这些公式看上去都好理解,但是反过来看呢?
我们遇到1,可以拆出好几个逻辑变量相加的形式,而这些都是我们后面证明公式用到的技巧!可不能小瞧它们
3.运算律

逻辑运算同样满足交换律(9,9‘),结合律(10,10’),分配律(11)
这里只解释不同于代数运算的特殊式子(11')

A + BC部分如左图所示,BC的交集与A的并集
A + C与A+ B两个集合想要得到左图,需要进行交集运算,对应逻辑与.
证明:(像这个公式的证明,就用到我们前面提到的,A·A = A的逆操作)
(A + B)(A + C) = A*A + B*A + A*C + B*C = A*(1 + B + C) + B*C= A + BC
4.德摩根定律
德摩根定律的证明用公式推不出来的,最简单的方式就是用真值表,直接将A,B所有取值列出来,判断左右两边式子是否结果相同
![]()
5.还原律
![]()
很容易理解,两次非运算后,得到的依旧是其本身.集合补集的补集依旧是该集合.
6.常用公式
(1)集合与子集合并公式(加大乘小)
A + AB = A (吸收律)
集合理解非常简单,加意味着取并集,那最终结果肯定为大的集合;
含义:一个与项是另一个与项的因子,则另一个与项可以被吸收掉(也就是消失).
Lg.(A + B) + (A + B)*C*D = A + B
同理,乘意味着取交集,那最终结果一定是小的集合.
A * (A + B) = A
整个公式可以记忆为"加大乘小"
(2)消因子公式
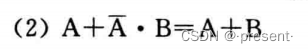
证明: A + B = (A +
) (A + B) = A + B
含义:在一个与或表达式中,如果一个与项的反是另一个与项的一个因子,则这个因子可以不要.
lg.![]()
(3)消项公式
![]()
证明:(这个公式证明就用到我们前面说的 = 1)
AB + C + BC(A +
) = (AB + BCA) + (
C + BC
) = (AB + ABC) + (
C +
CB)
= AB + C
PS:即便含BC组合而成的子项,也依旧可以消去. AB + C + BCD = AB +
C
lg.






















 2151
2151











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








