VERA : 一种比Lora更省资源的微调方案

❝

大家好，我是 Bob! 😊

一个想和大家慢慢变富的 AI 程序员💸

分享 AI 前沿技术、项目经验、面试技巧!

欢迎关注我，一起探索，一起破圈！💪

VERA论文笔记

❝

《 VERA VECTOR-BASED RANDOM MATRIX ADAPTATION 》

直达链接：

❝

https://arxiv.org/pdf/2310.11454

引言

该论文基于Lora，提出了基于向量的随机矩阵自适应（VeRA），与 LoRA 相比，它进一步减少了可训练参数的数量，但保持了相同的性能。模型达到了类似甚至更好的效果。

原理

 

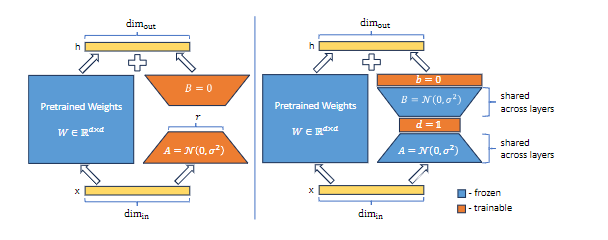
（图中蓝色部分为冻结部分，橙色为可训练部分）

1. LoRA 通过训练低秩矩阵 A 和 B 以及中间秩 r 来更新权重矩阵 W。

   h = W0x + ∆W x = W0x + BAx

1. 在 VeRA 中，这些矩阵被冻结（A B），在所有层之间共享，并使用可训练向量 d 和 b 进行调整，从而大大减少了可训练参数的数量。

   h = W0x + ∆W x = W0x + Λb B Λd A x

冻结一对随机初始化的矩阵，在所有适应层之间共享，并引入可训练的缩放向量，以实现逐层适应。

效果

参数量方面：

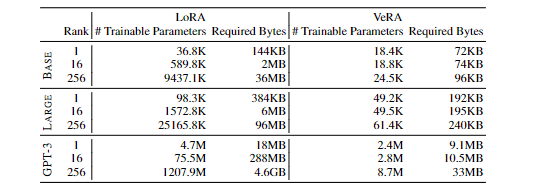
使用 L 表示微调层的数量，使用 d 表示这些层的维度。

VeRA 中可训练参数的数量 |θ| = L× (d+ r)

LoRA 的 |θ| = 2 × L × d × r

zi具体来说，对于最低秩（即 r = 1），VeRA 需要的可训练参数大约是 LoRA 的1/2。

随着秩 r 的增加，VeRA 的参数计数每次增加都会增加 L倍，与 LoRA 的 2Ld倍 相比，节省了很多。

显着减少了可训练参数的数量，这种参数效率在极深和极宽的模型中变得尤为重要

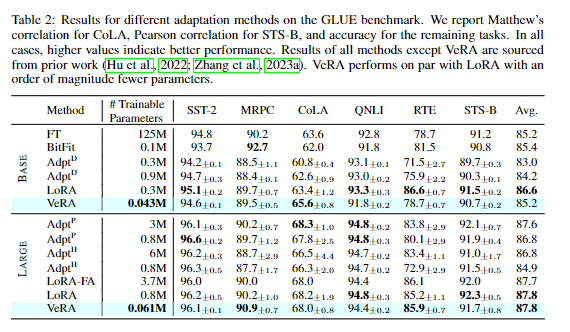
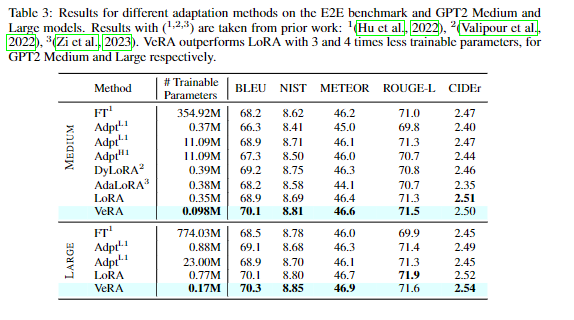
模型效果

在下游任务上产生类似或更好的结果

 

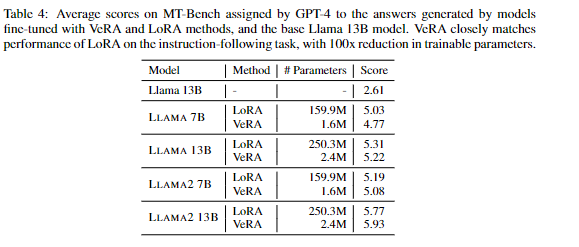
总结

论文引入了一种微调方法VERA，冻结一对随机初始化（A B）的矩阵，在所有适应层之间共享，并引入可训练的缩放向量( d b )，以实现逐层适应与 LoRA 相比，该方法显着减少了可训练参数的数量，从而在下游任务上产生类似或更好的结果.

 

Bob 的产品

1.【Bob 的 AI 成长陪伴群】

🔴AI 变现项目、AI 前沿技术、NLP 知识技术分享、前瞻思考、面试技巧、找工作等

🔴 个人 IP 打造、自媒体副业、向上社交、以及我的日常生活所见所闻，所思所想。

找一群人一起走，慢慢变富。期待和同频 ‮ 朋的 ‬ 友一起蜕变！

扫码加微信，链接不迷路！