MATLAB新手实验(2)--语言矩阵运算

MATLAB新手实验(2)–语言矩阵运算

1、下列运算是否合法，为什么？如合法，结果是多少？

(1) result1 = a’
(2) result2 = a * b
(3) result3 = a + b
(4) result4 = b * d
(5) result5 = [b ; c’ ] * d
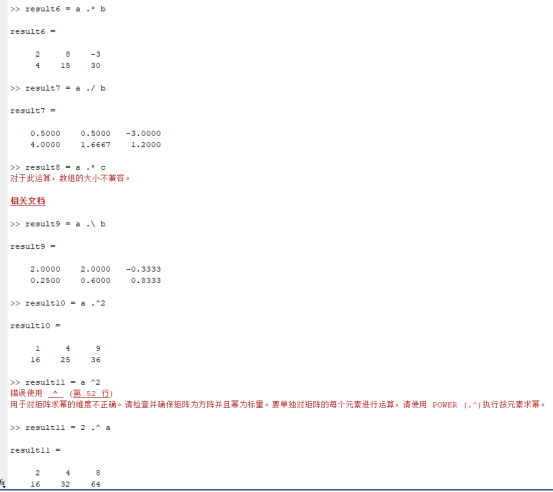
(6) result6 = a . * b
(7) result7 = a . / b
(8) result8 = a . * c
(9) result9 = a . \ b
(10) result10 = a . ^2
(11) result11 = a ^2
(12) result11 = 2 . ^ a

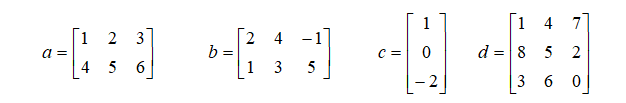
首先定义给定的矩阵：

a = [1 2 3; 4 5 6];
b = [2 4 -1; 1 3 5];
c = [1; 0; -2];
d = [1 4 7; 8 5 2; 3 6 0];

a’ 合法 转置矩阵
ab 不合法 维度不匹配(2×3)(2×3)
a+b 合法 对应元素相加
b*d 合法 结果2×3矩阵
[b;c’]*d 不合法 垂直拼接维度不匹配
a.*b 合法 元素乘法
a./b 合法 元素除法(注意除0)
a.*c 不合法 维度不匹配
a.\b 合法 等价于b./a
a.^2 合法 每个元素平方
a^2 不合法 非方阵不能幂运算
2.^a 合法 2的各元素次方

2、用MATLAB求下面的的方程组。

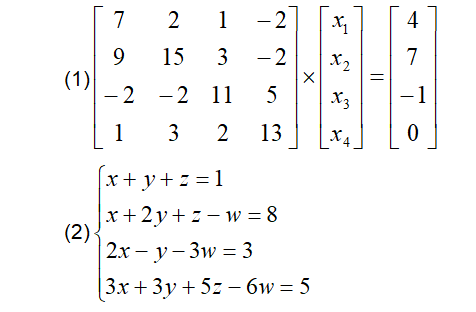
A = [7 2 1 -2; 9 15 3 -2; -2 -2 11 5; 1 3 2 13];
b = [4; 7; -1; 0];
x = A\b;
disp('解为:');
disp(x);

A = [1 1 1 0; 1 2 1 -1; 2 -1 0 -3; 3 3 5 -6];
b = [1; 8; 3; 5];
x = A\b;
disp('解为:');
disp(x);

3、求矩阵A的秩(rank),求矩阵A的行列式(determinant),求矩阵A的逆(inverse),求矩阵A的特征值及特征向量(eigenvalue and eigenvector)

A = [7 2 1 -2; 9 15 3 -2; -2 -2 11 5; 1 3 2 13];

% (1) 矩阵的秩
r = rank(A);
disp(['矩阵的秩: ', num2str(r)]);

% (2) 行列式
d = det(A);
disp(['行列式: ', num2str(d)]);

% (3) 逆矩阵
inv_A = inv(A);
disp('逆矩阵:');
disp(inv_A);

% (4) 特征值和特征向量
[eig_vec, eig_val] = eig(A);
disp('特征值:');
disp(diag(eig_val)');
disp('特征向量:');
disp(eig_vec);

4、关系运算与逻辑运算

已知a=20,b=-2,c=0,d=1
(1) r1 = a > b
(2) r2 = a > b & c > d
(3) r3 = a == b* (-10)
(4) r4 = ~b | c

a = 20; b = -2; c = 0; d = 1;

% (1) r1 = a > b
r1 = a > b;
disp(['r1 = ', num2str(r1)]);

% (2) r2 = a > b & c > d
r2 = a > b & c > d;
disp(['r2 = ', num2str(r2)]);

% (3) r3 = a == b^(-10)
r3 = a == b*(-10);
disp(['r3 = ', num2str(r3)]);

% (4) r4 = ~b | c
r4 = ~b | c;
disp(['r4 = ', num2str(r4)]);

5、思考题

% 初始化和为 0
y = 0;
% 循环计算从 n = -10 到 n = 10 的和
for n = -10:10
    y = y + 2^n;
end
% 使用 format long 显示长精度数值
format long
disp(y);