阿白数模笔记之蒙特卡罗方法（Monte Carlo Method）

前言

        还记得浦丰投针实验吗？

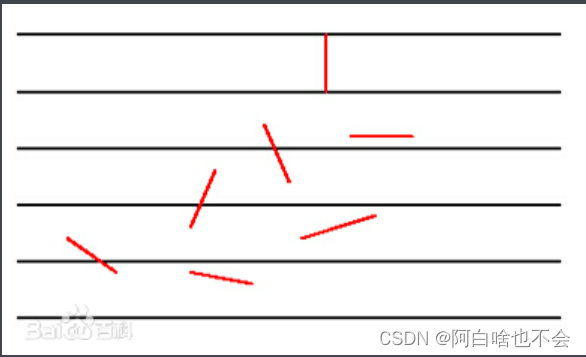
浦丰所进行的是一个概率实验（Probability experiment），这样的方法称为蒙特卡罗方法（Monte Carlo Method）。而蒙特卡罗（Monte Carlo）是世界著名的“赌城”，世界三大赌城之一（美国超级赌城拉斯维加斯与号称东方拉斯维加斯的中国澳门）。事实上还有拉斯维加斯方法（本文不涉及）。

        本文将通过几个案例解释蒙特卡罗方法的原理和应用。

案例一

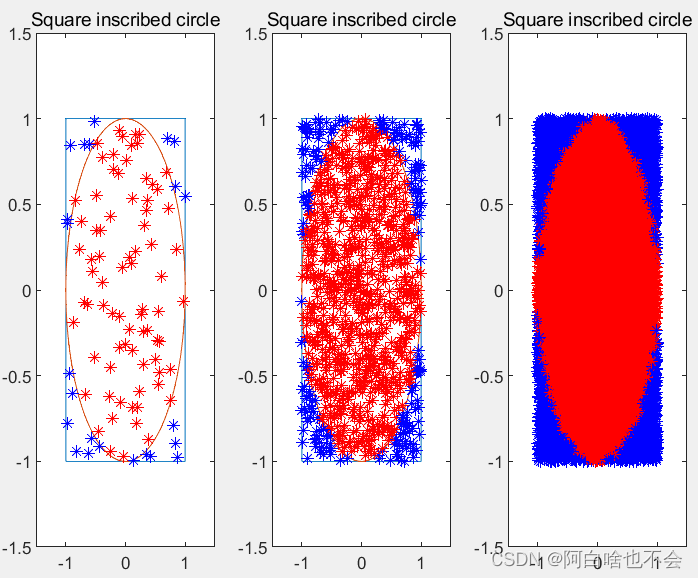
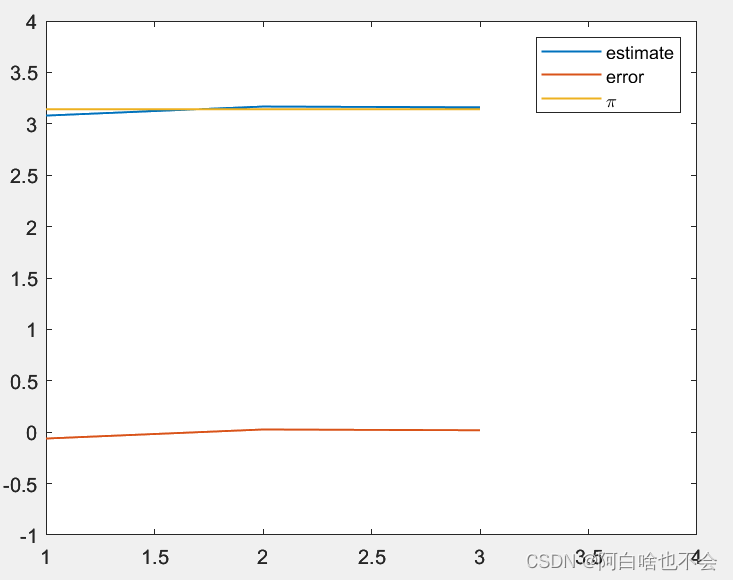
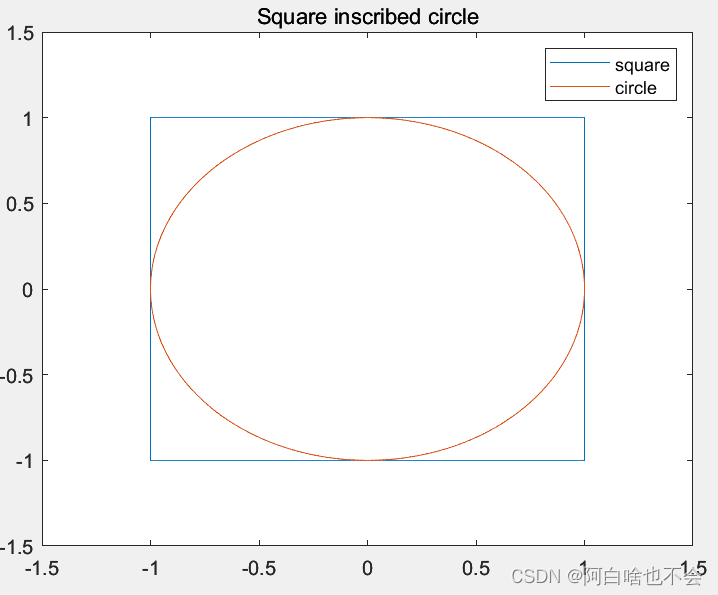往正方形区域D={(x,y):x∈[−1,1],y∈[−1,1]}内生成随机点，在单位圆区域C={(x,y):x2+y2≤1}内的点和点的总数之比近似为~pi/4。随着实验样本总数的改变，结果越来越精确，不加证明的给出此例中增加一位小数精度需使用100倍的样本数。MATLAB实现如下：

①绘制图形

x=[1,-1,-1,1,1];
y=[1,1,-1,-1,1];%将正方体的角连起来
t=linspace(0,2*pi,1000);
x1=cos(t);y1=sin(t);
plot(x,y,x1,y1);
legend('square','circle')
title('Square inscribed circle')
axis([-1.5 1.5 -1.5 1.5]);

②生成随机点列

xt=unifrnd(-1,1,[n,1]);%testblock&times
yt=unifrnd(-1,1,[n,1]);

③筛选计数

k=0;
for i=1:n
    if (xt(i,1)^2+yt(i,1)^2)<=1
        k=k+1;
        scatter(xt(i,1),yt(i,1),'r*')
    else
        scatter(xt(i,1),yt(i,1),'b*')
    end
end
p=4*k/n;%估计值
e=p-pi;%误差

④精度分析

案例二

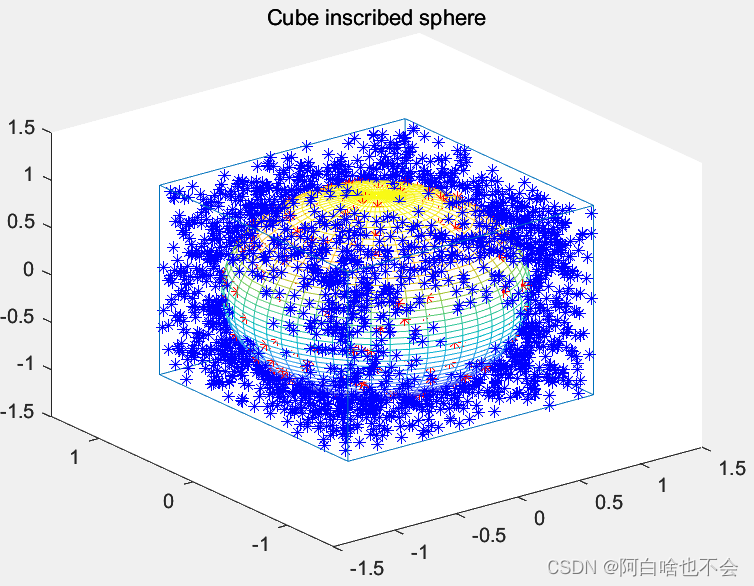      Monte Carlo method 对维数并不敏感，可被用来计算多重积分。左图是计算球的面积

x=[1,1,1,1,1,-1,-1,-1,-1,-1,-1,1,1,-1,-1,1];
y=[-1,-1,1,1,-1,-1,-1,1,1,-1,-1,-1,1,1,1,1];
z=[1,-1,-1,1,1,1,-1,-1,1,1,-1,-1,-1,-1,1,1];
plot3(x,y,z);%绘制正方体
axis([-1.5,1.5,-1.5,1.5,-1.5,1.5]);
hold on;
n=5000;
[x1,y1,z1]=sphere(50);%绘制球体
mesh(x1,y1,z1);
title('Cube inscribed sphere');
xt=unifrnd(-1,1,[n,1]);%testblock&times
yt=unifrnd(-1,1,[n,1]);
zt=unifrnd(-1,1,[n,1]);
k=0;
for i=1:n
    if (xt(i)^2+yt(i)^2+zt(i)^2)<=1
        scatter3(xt(i),yt(i),zt(i),'r*')
        k=k+1;
    else
        scatter3(xt(i),yt(i),zt(i),'b*')
    end
end
p=k/n*6;
e=p-pi;

案例三

下面利用Monte Carlo method求解浦丰投针问题:

考虑针的中点x位置，不妨设,a是平行线簇的间距，设针与平行线所成角度为，则当针与线相交时，,针落在线上的概率为，再利用Monte Carlo方法计算积分值即知

为方便计算，取

plot([0,pi],[1,1],'linewidth',2);
t=linspace(0,pi,1000);
y=0.5*sin(t);
hold on
plot(t,y);
n=10000;
x1=unifrnd(0,pi,[n,1]);
y1=unifrnd(0,1,[n,1]);
k=0;
for i=1:n
    if y1(i)<0.5*sin(x1(i))
        k=k+1;
        scatter(x1(i),y1(i),'r*')
    else
        scatter(x1(i),y1(i),'b*')
    end
end
axis([0,pi,0,1]);
p=n/k;
e=p-pi;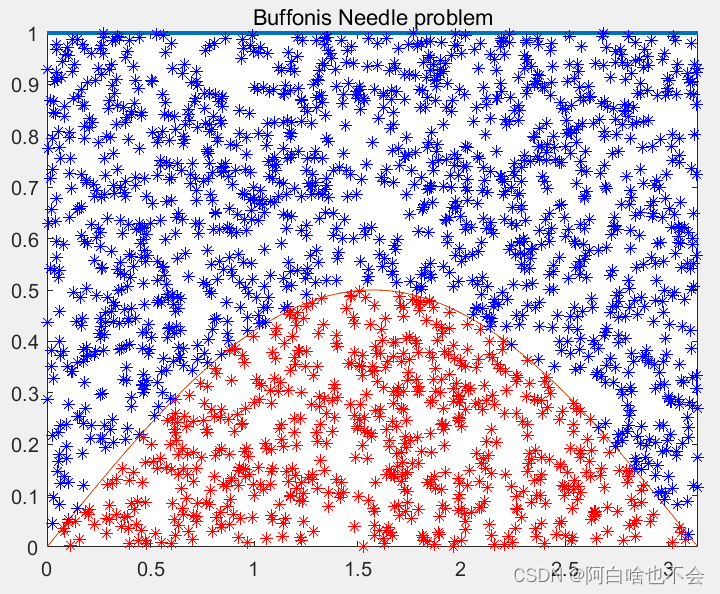

总结

        案例一，二是Monte Carlo method在二维，三维的应用，没有本质差别（维数对Monte Carlo method影响很小），案例三是先用数学方法从概率实验中抽离出待求式再通过Monte Carlo method计算。而Monte Carlo 的缺点也很明显：1.对于确定性问题需要转化成随机性问题。2.误差是概率误差。3.通常需要较多的计算步数N.