这是一个简单的小案例,利用季节性移动平均模型(SARIMA)对2024年新能源汽车的产销量进行分析,大家可以简单了解一下如何使用这个模型对有周期性的时序数据进行预测分析,本篇博客用于学习记录。
SARIMA模型是ARIMA模型的扩展,用于处理具有明显季节性变化的时间序列数据。它在ARIMA模型的基础上添加了季节性成分,以更好地捕捉季节性变化的影响。当然季节性不仅局限于一年四季这种自然季节的周期性变化,任何类型的周期性都可以。比如说季节性可以是一天内的小时变化(24)、一周内的星期变化(7)、一个月内的日变化(30)、一年内的月变化(12)。
本例就是利用2015年-2023年的新能源汽车月产销量来预测2024年的月产销量,一个周期便是12个月。
SARIMA模型介绍可以看看这个博主写的,很详细:季节性时间序列预测之SARIMA模型
下面开始我们的小案例吧!!!
先导入咱们需要用的库,我的代码是在jupyter notebook运行的。
import pandas as pd
import numpy as np
# 基本的数据处理包
import matplotlib.pyplot as plt
import seaborn as sns
# 这两段是为了绘制小提琴图
from tqdm import tqdm # 导入 tqdm 库,给网格搜索的时候加进度条
from pyecharts.globals import CurrentConfig, NotebookType
CurrentConfig.NOTEBOOK_TYPE = NotebookType.JUPYTER_LAB
# 加上面这两段代码是为了让jupyter notebook能显示所作的图像
import pyecharts.options as opts
from pyecharts.charts import Line, Radar, Scatter
from pyecharts.globals import ThemeType
# 本实验最重要的绘图工具
import itertools
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error
# 调用SARIMA模型需要的包
1. 数据读入
# 按月读取2015年1月1日-2024年3月1日的数据
df1 = pd.read_excel("2014-2024年新能源汽车产销量(月).xlsx", sheet_name = 0)
def date(para):
if type(para) == int:
delta = pd.Timedelta(str(int(para))+'days')
time = pd.to_datetime('1899-12-30') + delta
return time
else:
return para
df1['时间'] = df1['时间'].apply(date)
df1.set_index('时间', inplace=True)
df1.index = pd.DatetimeIndex(df1.index).to_period('M')# 设置周期频率2. 检测空缺值
绘制产销量曲线——这里推荐大家作图可以试试pyecharts,好用图也好看!!!
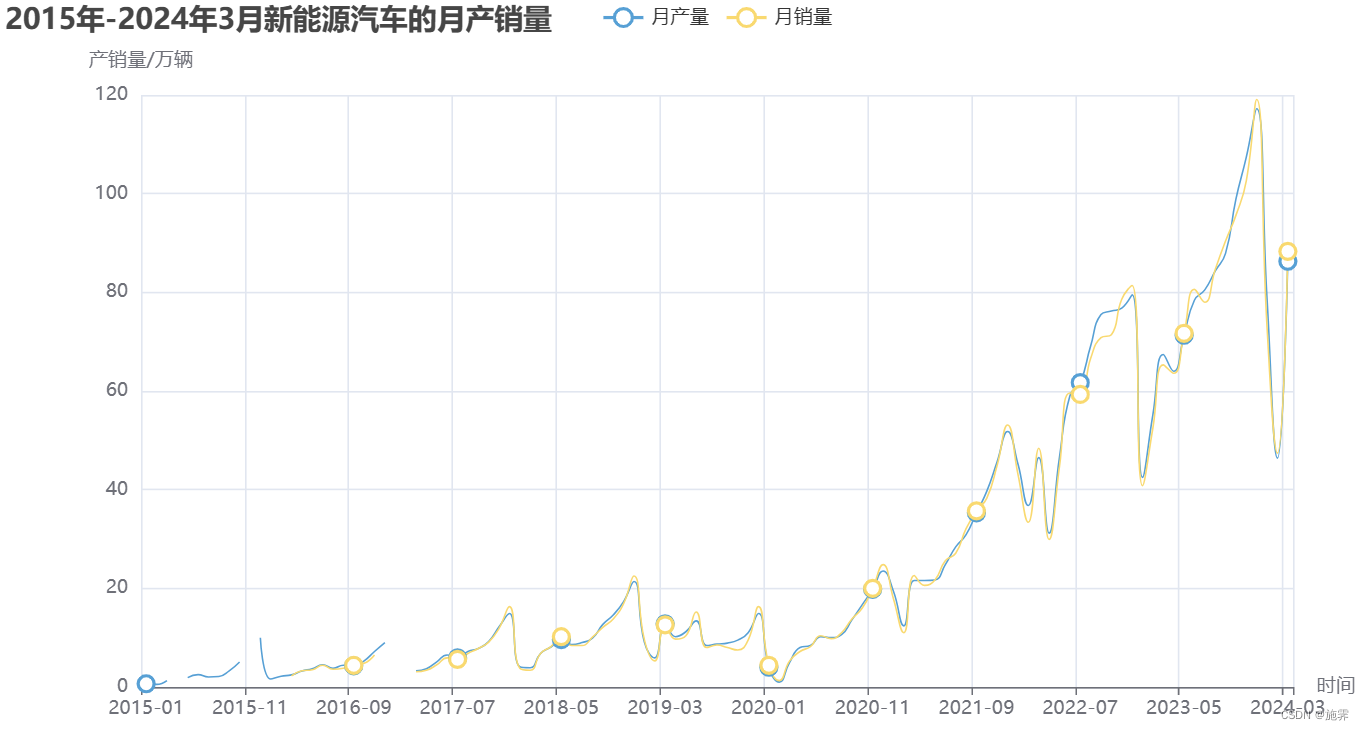
通过绘制图像可以看到在2015-2017年之间存在明显的断点,并且数据与时间有相关性,初步考虑利用季节性移动平均模型(SARIMA)填补空缺值,并利用该模型对2024年的新能源汽车的产销量进行预测分析;
代码实现:
# 将周期对象转换为字符串形式
x_axis_data = [str(period) for period in df1.index.tolist()]
yields = (
Line(init_opts=opts.InitOpts(theme=ThemeType.LIGHT))
.add_xaxis(x_axis_data)
.add_yaxis(series_name="月产量",
is_smooth=True,
y_axis=df1['产量(万辆)'].tolist(),
symbol_size=10,
# linestyle_opts=opts.LineStyleOpts(color="blue"),
label_opts=opts.LabelOpts(is_show=False))
.add_yaxis(series_name="月销量",
is_smooth=True,
y_axis=df1['销量(万辆)'].tolist(),
symbol_size=10,
# linestyle_opts=opts.LineStyleOpts(color="blue"),
label_opts=opts.LabelOpts(is_show=False))
.set_global_opts(title_opts=opts.TitleOpts(title="2015年-2024年3月新能源汽车的月产销量"),
xaxis_opts=opts.AxisOpts(type_='category', name="时间"),
yaxis_opts=opts.AxisOpts(type_='value', name="产销量/万辆"),
)
)
yields.load_javascript()
yields.render_notebook()3. 检测异常值
绘制小提琴图——这里推荐使用小提琴图,因为小提琴图相较于箱线图更加好看,而且在数模比赛中也很受青睐!!!
 根据小提琴图可以看到,产销量的取值集中分布在[0,25]这个区间内,并且两个小提琴图十分相似,峰值几乎相等,和我国新能源汽车的发展趋势相符,不考虑进行异常值剔除。
根据小提琴图可以看到,产销量的取值集中分布在[0,25]这个区间内,并且两个小提琴图十分相似,峰值几乎相等,和我国新能源汽车的发展趋势相符,不考虑进行异常值剔除。
代码实现:
custom_palette = ["#ff7f0e", "#2ca02c"]
# 绘制小提琴图,并指定调色板
sns.violinplot(data=df1, inner="quartile", palette=custom_palette)
plt.title('产销量小提琴图')
plt.xlabel('Groups')
plt.ylabel('Values')
plt.show()4. 检测每年月销量的平稳性
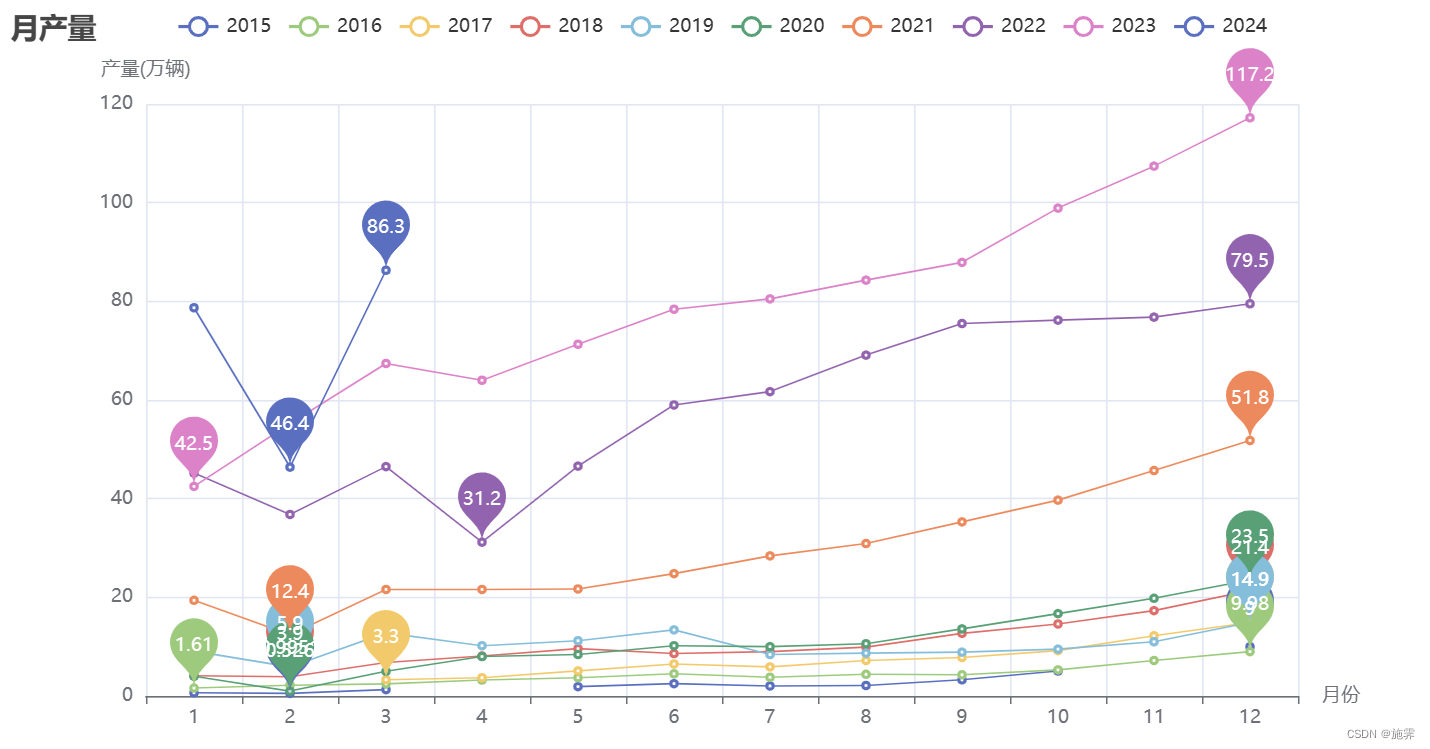
我国于2014年发行了新能源汽车的相关政策,根据上图可以看到,在2020年以前,新能源汽车的月产量均在25万辆以下,并且发展趋势也相对平缓。2020年以后,受疫情的影响,产量会有所波动,但总体成上升趋势,从2021年开始有了明显的提升,在2022-2024年得到了迅速的发展!
代码实现:
# 导入数据
sales_data = [df1['产量(万辆)'].tolist()[i*12: (i+1)*12] for i in range(10)]
# 提取年份
years = [str(i) for i in range(2015, 2025)]
# 初始化 Line 对象
line = Line()
# 添加折线数据
for year, sales in zip(years, sales_data):
line.add_xaxis(range(1, 13))
line.add_yaxis(f"{year}", sales)
# 设置全局参数
line.set_global_opts(
title_opts=opts.TitleOpts(title="月产量"),
xaxis_opts=opts.AxisOpts(type_="category", name="月份"),
yaxis_opts=opts.AxisOpts(name="产量(万辆)"),
tooltip_opts=opts.TooltipOpts(trigger="axis", axis_pointer_type="cross"),
legend_opts=opts.LegendOpts(pos_left="center", orient="horizontal")
)
line.load_javascript()
line.render_notebook()5. SARIMA建模
根据获取到的2015-2024年新能源汽车月销售数据,建立SARIMA模型,同时为了避免空缺值对模型造成的影响,考虑利用完整年份的数据进行建模;
建模步骤如下:
- 获取2015-2024年新能源汽车产销量数据,对时间列索引转化为以月份为单位的周期索引;
- 初步限定SARIMA模型参数p、d、q的参数范围,利用网格搜索法计算每组参数的均方根误差,并实时选取误差最小的参数组;
- 选取最优参数进行模型拟合,设置SARIMA模型的周期为12,带入原始日期进行拟合并可视化;
- 设置预测日期为2024年1月到2024年12月,利用训练好的模型进行预测,可视化预测结果。
首先是对新能源汽车产量的拟合。在第一步利用to_period()函数将获取的数据日期索引更改为按月为单位的周期索引,设置p的参数范围为(0,5), d的参数范围为(0,3), q的参数范围为(0,5),通过for循环对计算每组参数值的RMSE,最终得到SARIMA模型的最优参数为(2,1,4)。
代码实现:
train = df1[:108] # 选取完整的时序数据
# 定义参数范围
p_range = range(0, 5) # 自回归阶数范围
d_range = range(0, 3) # 差分阶数范围
q_range = range(0, 5) # 移动平均阶数范围
parameters = itertools.product(p_range, d_range, q_range)
best_score = float('inf')
best_params = None
# 网格搜索
for param in tqdm(parameters, total=len(p_range)*len(d_range)*len(q_range)):
try:
# 使用当前参数拟合 SARIMA 模型
model = SARIMAX(train['产量(万辆)'], order=param, seasonal_order=(1, 1, 1, 12))
result = model.fit()
# 计算模型的均方根误差(RMSE)
predicted_sales = result.predict(start=train.index[0], end=train.index[-1])
rmse = np.sqrt(mean_squared_error(train['产量(万辆)'], predicted_sales))
# 打印RMSE
print("RMSE:", rmse)
# 更新最优参数
if rmse < best_score:
best_score = rmse
best_params = param
except:
continue
print("Best Parameters:", best_params)
# 将 PeriodIndex 转换为 Timestamp 格式
predicted_index = df3.index.to_timestamp()
# 使用 SARIMA 模型进行产量拟合和预测
model = SARIMAX(train['产量(万辆)'], order=(2, 1, 4), seasonal_order=(1, 1, 1, 12))
result = model.fit()
# 预测
predicted_yields = result.predict(start=predicted_index[0], end=predicted_index[-1])
predicted_yields 调用statsmodels库中的SARIMA模型,设置周期为12个月,然后进行模型的训练,拟合结果如下:
代码实现:
# 将周期对象转换为字符串形式
x_axis_data = [str(period) for period in df1.index.tolist()]
predict = (
Line(init_opts=opts.InitOpts(theme=ThemeType.LIGHT))
.add_xaxis(x_axis_data)
.add_yaxis(series_name="月产量",
is_smooth=True,
y_axis=df3['产量(万辆)'].tolist(),
symbol_size=10,
# linestyle_opts=opts.LineStyleOpts(color="pink"),
label_opts=opts.LabelOpts(is_show=False))
.add_yaxis(series_name="预测产量",
is_smooth=True,
y_axis=predicted_sales.tolist(),
symbol_size=10,
linestyle_opts=opts.LineStyleOpts(color="red"),
label_opts=opts.LabelOpts(is_show=False))
.set_global_opts(title_opts=opts.TitleOpts(title="2015年-2024年3月新能源汽车的月产销量"),
xaxis_opts=opts.AxisOpts(type_='category', name="时间"),
yaxis_opts=opts.AxisOpts(type_='value', name="产量/万辆"),
)
)
predict.load_javascript()
predict.render_notebook()可以看到,预测曲线基本拟合了原始图像,下面设定预测区间为2024年1月到2024年12月,2024年每月新能源汽车产量效果图如下:

代码实现:
# 预测未来2024年的产量变化
predicted_2024 = result.predict(start='2024-01', end='2024-12', freq='M')
predicted_2024 = [round(i, 2) for i in predicted_2024]
# 将周期对象转换为字符串形式
x_axis_data = [f'2024-{i}' for i in range(1, 13)]
predict_2024 = (
Line(init_opts=opts.InitOpts(theme=ThemeType.LIGHT))
.add_xaxis(x_axis_data)
.add_yaxis(series_name="预测产量",
is_smooth=True,
y_axis=predicted_2024,
symbol_size=10,
label_opts=opts.LabelOpts(is_show=True))
.set_global_opts(title_opts=opts.TitleOpts(title="2024年新能源汽车的月产量"),
xaxis_opts=opts.AxisOpts(type_='category', name="时间"),
yaxis_opts=opts.AxisOpts(type_='value', name="产量/万辆"),
)
)
predict_2024.load_javascript()
predict_2024.render_notebook()Over!晚安家人们,好梦啦~

























 565
565

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










