z变换及z变换性质运用和总结

1. z变换的概念

1.1 z变换

$f(k)$的双边z变换：

$F(z)={\sum }_{k=-\infty }^{\infty }f(k)z^{-k}$
双边z变换，k的范围为$-\infty 到\infty$

$f(k)$的单边变换：

$F(z)={\sum }_{k=0}^{\infty }f(k)z^{-}k$
单边z变换，k的范围为0到$\infty$

注意公式中z是-k次幂
对于$f(k)和F(z)之间的关系简记为：$

$f(k)\leftrightarrow F(z)$

1.2 收敛域

因果序列

所以对于因果序列收敛域$|z|>|a|$是半径为$|a|$的圆外区域（如上图阴影部分）

反因果序列

所以对于反因果序列仅当$|z|<|b|$时，其$z变换存在，收敛域是半径为|b|的圆内区域$

1.3 双边序列

1.4 结论：

1.5常用序列z变换

2. z变换的性质

2.1 线性

线性很好理解，

2.2 移位（移序）特性

双边相对简单，只需要在$z变换上乘上z^{\pm m}即可$
而单边则可以对着概念对比记忆一下

例题：

2.3 z域尺度变换（序列乘$a^k$）

通过例题来理解一下

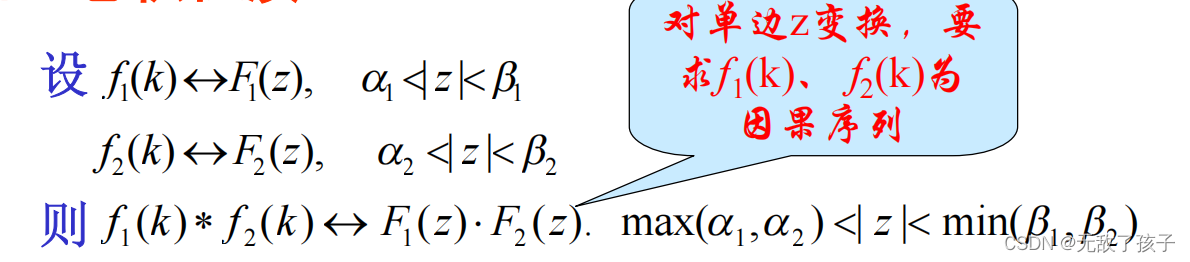
2.4 卷积性质

2.5 z域微分（序列乘k）

2.5 z域积分（序列除k+m）

2.7 k域反转

令$b=\frac{1}{a},上式可写为$
$b^k\epsilon (-k-1)\leftrightarrow \frac{-z}{z-b}$

尽量记住上图最后一个结果和这个写的这个$b=\frac{1}{a}的z变换$

2.8 部分和

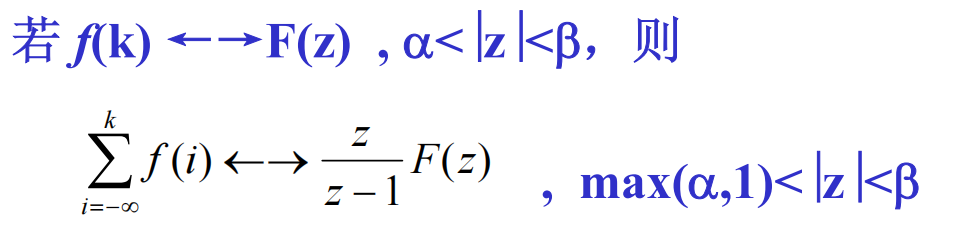
2.9 初值定理和终值定理

这里求和上限不再是到$\infty 而是到k，只求了一部分的和，所以叫部分和公式$

2.9.1 初值定理

2.9.2 终值定理

因为此处的$z是取极限，无限趋近于1，所以{\lim }_{z\to 1}\frac{z-1}{z}F(z)={\lim }_{z\to 1}(z-1)F(z)$

解：