在码分复用中,每个用户的码分序列与其他用户的序列是相互正交的,以确保每个用户的信号可以被正确地解调和恢复。为了实现这一点,通常使用以下方法:
1. 沃尔什-哈达玛码(Walsh-Hadamard codes):沃尔什-哈达玛码是一种二进制正交码,由沃尔什函数和哈达玛矩阵组成。这些码具有良好的自相关和互相关特性,使得它们在码分复用中得到了广泛的应用。
2. 伪随机码(Pseudonoise codes):伪随机码是一种看似随机但实际上是确定性的码序列。这些码可以通过移位寄存器或其他生成方法来生成,并且具有良好的自相关和互相关特性。
3. 扩频码(Spread spectrum codes):扩频码是一种将信号扩展到更宽的频带的技术。在码分复用中,每个用户使用一个唯一的扩频码来调制其信号。这些扩频码可以是伪随机码或其他类型的码,并且具有良好的自相关和互相关特性。
通过使用这些相互正交的码分序列,每个用户的信号可以在接收端被正确地解调和恢复,实现多个用户在同一频率或时间资源上同时传输信号。
扩频码是一种将信号扩展到更宽的频带的技术。扩频码可以是伪随机码。扩频码的主要目的是将信号扩展到更宽的频带,从而降低信号功率谱密度,提高系统的抗干扰能力。
伪随机码是一种看似随机,但实际上是确定性的码序列。伪随机码可以通过移位寄存器或其他生成方法来生成。通常用于通信加密、纠错和信号调制。沃尔什-哈达玛码:沃尔什函数和哈达玛矩阵沃尔什排序的沃尔什函数(列率排列)
沃尔什-哈达玛码:沃尔什函数和哈达玛矩阵
沃尔什排序的沃尔什函数(列率排列)
其中,R(k+1,t)是任意rademacher函数,g(i)是i的格雷码, g(i)k是此格雷码的第k位数。P为正整数




佩利排序的沃尔什函数

其中,R(k+1,t)是任意拉德梅克函数,ik是自然二进制码的第k位数。P为正整数


哈达玛排序的沃尔什函数

其中,R(k+1,t)是任意拉德梅克函数, ik是倒序的二进制码的第k位数。P为正整数


高阶矩阵可用两个低阶矩阵的克罗内克积(Kronecker Product)求得
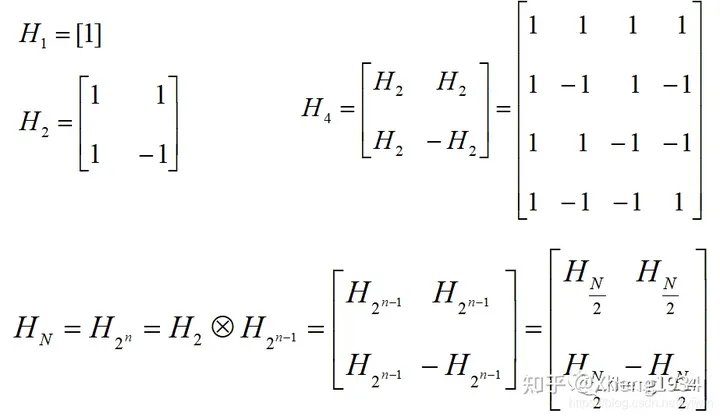
哈达玛矩阵的最大优点在于它具有简单的递推关系,即高阶矩阵可用两个低阶矩阵的克罗内克积(Kronecker Product)求得。因此常采用哈达玛排列定义的沃尔什变换。(格雷码:在一组数的编码中,若任意两个相邻的代码只有一位二进制数不同,则称这种编码为格雷码,另外由于最大数与最小数之间也仅一位数不同,即“首尾相连”,因此又称循环码或反射码。)

在CDMA 通信系统中,基站将信号发送给所有用户,每个用户使用自己的扩频码或伪随机码来调制接收到的信号。然后,每个用户将调制后的信号发送回基站。基站使用每个用户的扩频码或伪随机码来解调和恢复每个用户的原始信号。通过使用扩频码或伪随机码,CDMA通信系统可以实现多个用户在同一频率或时间资源上同时传输信号,从而提高了系统的容量和效率。此外,扩频码或伪随机码的使用还可以提高系统的抗干扰能力,因为它们将信号扩展到更宽的频带,使得干扰信号的功率谱密度降低。干扰信号功率谱密度是指干扰信号在频域上的功率分布情况。它是干扰信号在每个频率点上的功率与该频率点带宽的比值,通常用单位为瓦特/赫兹(W/Hz)来表示。干扰信号功率谱密度的大小取决于干扰信号的强度和带宽。较强的干扰信号将具有较高的功率谱密度,而较宽的带宽将导致功率谱密度在更宽的频率范围内分布。在通信系统中,干扰信号功率谱密度是一个重要的参数,因为它会影响系统的抗干扰能力和通信质量。较高的干扰信号功率谱密度会降低系统的信噪比,从而降低通信质量。因此,在设计通信系统时,需要考虑干扰信号功率谱密度,并采取适当的抗干扰措施来提高系统的抗干扰能力。

























 776
776

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








