α-β剪枝算法

dasi0227

已于 2024-04-28 15:29:36 修改

阅读量4.7k

点赞数 32

文章标签：算法剪枝人工智能 python

于 2024-04-28 15:24:53 首次发布

本文链接：https://blog.csdn.net/m0_74766888/article/details/136971081

版权

一、前言

理解了很久α-β剪枝过程，特写此篇加深理解，并讲清楚算法的具体流程。如有错误、建议和优化欢迎指出！

二、博弈

（1）前提

双人博弈：博弈对象只有己方和对方，没有第三方
二人零和：若一方获胜取得x分，则另一方失败取得-x分
全信息：博弈过程中，任何一方都完全了解当前格局和过去历史，不存在信息差
非偶然：任何一方都只能根据当前实际情况来采取行动，不存在“碰运气”的行为
利益完全对立：任何一方动作的目的都只能是击败对方，不存在暂时合作
交替行动：每方一次只能进行一次动作，接着就轮到对方做动作

（2）博弈树

根结点：博弈的初始状态
叶子结点：博弈的终止状态
边：可能的行动
效益值：每个终止状态对一方的有利程度和对另一方的不利程度
估值函数e(p)：根据当前状态p和博弈规则，给出当前结点p的效益值
深度：计算当前状态的效益值所需要向下参考的子树层数

三、极大极小分析法

零和：若己方的效益值为x则对方的效益值为-x，因此只需考虑其中一方的的效益值

倒推法：自底向上，根据子结点的效益值确定父结点的效益值，且叶子结点的效益值是已知的

博弈目的：若将己方作为根结点要获胜，则己方每次选择都要追求最大的效益值，而对方每次选择都要追求最小的效益值

MAX结点：己方做选择的层的全部结点，总是选择效益值最大的子结点-->对己方最有利（极大的含义）
MIN结点：对方做选择的层的全部结点，总是选择效益值最小的子结点-->对己方最不利（极小的含义）

四、α-β剪枝

（1）基本概念

极大极小算法的局限性：必须算出全部子结点结点的效益值才能判断父节点的效益值
极大极小算法的优化：及时剪掉无用的子结点分枝，仅根据部分子结点就可以得到父节点的效益值
MAX结点：
- α值：MAX结点的子结点的最大值
- β值：MAX结点的左边/已遍历兄弟结点的最小值
MIN结点：
- α值：MIN结点的左边/已遍历兄弟结点的最大值
- β值：MIN结点的子结点的最小值

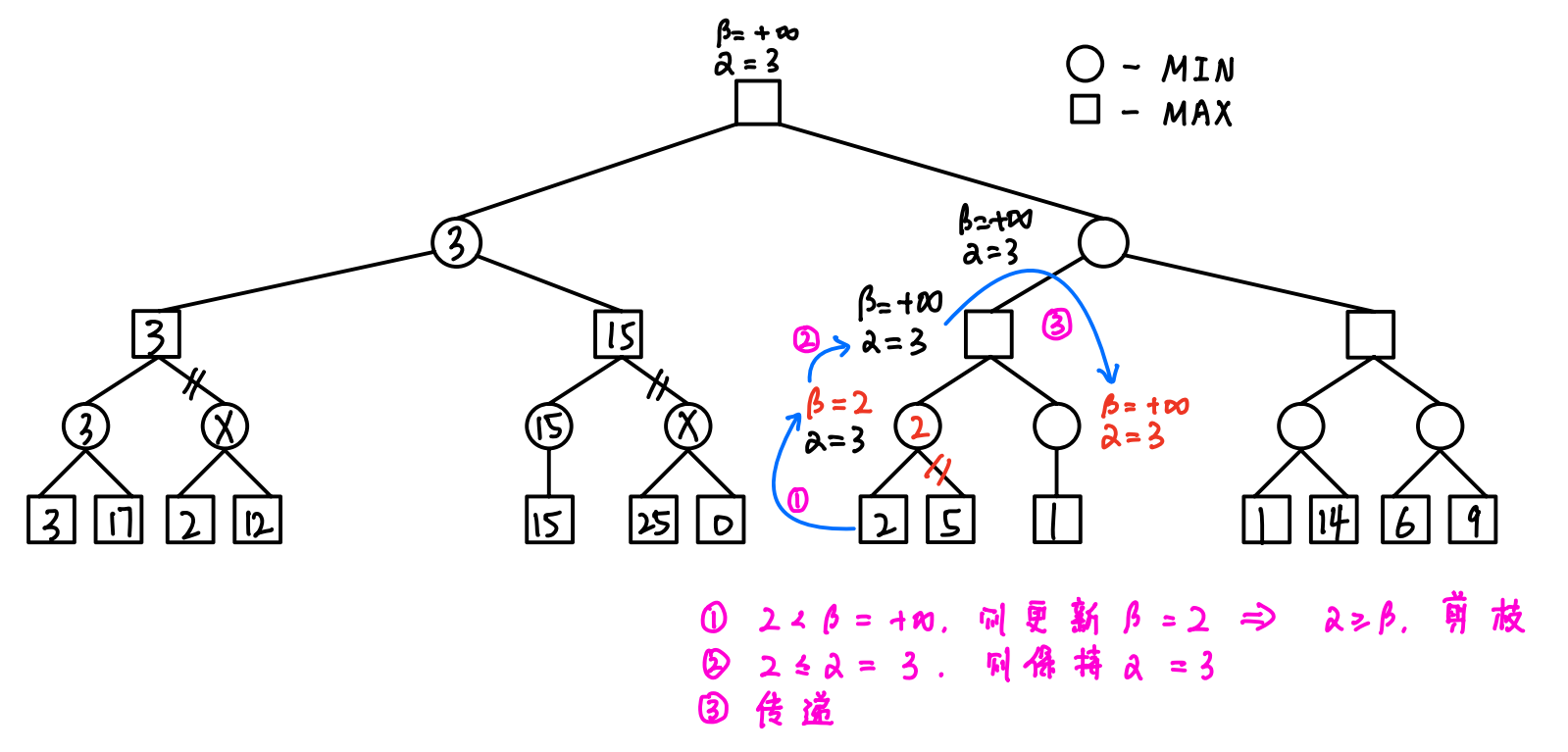
（2）α剪枝--删除以MAX结点为根结点的分支

剪枝原理：MAX结点选择最大值，但MAX结点的父结点是MIN结点要选择最小值，如果存在α>β即该MAX结点最终取值一定≥α，因此MIN结点会暂时选择β分支，而不会考虑α分支（所以才叫α-cuts）

（3）β剪枝--删除以MIN结点为根结点的分支

剪枝原理：MIN结点选择最小值，但MIN结点的父结点是MAX结点要选择最大值，如果存在α>β即该MIN结点最终取值一定≤β，因此MAX结点会暂时选择α分支，而不会考虑β分支（所以才叫β-cuts）

（4）α-β剪枝算法分析

1. 算法的操作

初始化：令根节点的α=-∞，β=+∞
传递（从上往下）：将父结点α值和β值都赋给子结点
回溯（从下往上）：父MAX结点的α值 = 子MIN结点的β值，父MIN结点的β值 = 子MAX结点的α值
剪枝（从左往右）：如果结点更新后的α≥β，则剪去以该结点为根结点的分支

2. 操作的理解（赋值原理）

回溯的单一赋值：MAX的β值与子结点无关，MIN的α值与子结点无关
回溯的交叉赋值：
- 父MAX的α值取决于子MIN，子MIN根据β取值
- 父MIN的β值取决于子MAX，子MAX根据α取值
传递的对应赋值：
- MAX的子结点最大值 = 子结点已遍历兄弟结点的最大值 --> 父MAX结点的α值与子MIN结点的α值是相同的
- MIN的子结点最小值 = 子结点已遍历兄弟结点的最小值 --> 父MIN结点的β值与子MAX结点MAX的β值是相同的
虽然MAX和MIN结点的α值和β值的意义不一样，但是观察发现上述α-cut和β-cut的前提都是α≥β

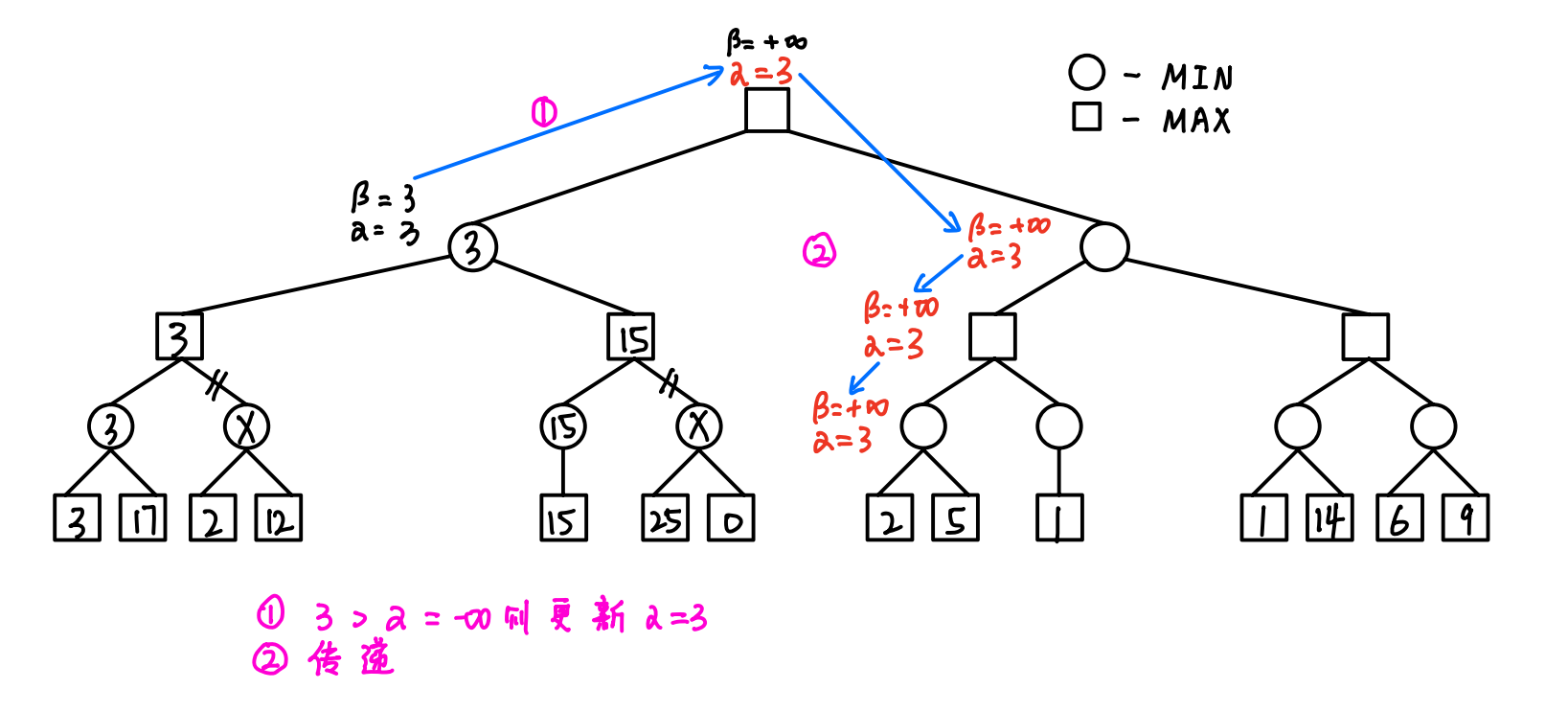
3. 算法的流程（详细图解）

令根结点的α = +∞，β = -∞，然后逐渐向下传递，直到遇到第一个叶子结点
反复进行以下三步：
1. 传递：根据父结点更新子结点 -> 成对对应赋值
2. 回溯：根据子结点更新父结点 -> 单一交叉赋值
3. 剪枝：一旦出现α ≥ β的情况，及时剪枝
得到根结点的效益值，并选择对应的子结点作为下一次扩展的根结点

（5）α-β算法的伪代码

全局设置最大深度maxdepth

主函数调用 alpha-beta(node = root, a = -∞, β = +∞, flag = 'MAX', depth = 0)

如果当前结点到达最大深度，即depth == maxdepth：返回当前结点的评估函数值
如果当前结点是最优状态，返回+∞
如果当前结点时最坏状态，返回-∞
如果当前结点是MAX结点，即flag = 'MAX'：
α = 传递值，β = 传递值
遍历每个子结点subnode：
调用 alpha-beta(subnode, a, β, 'MIN', depth+1)，得到返回值x
若x > α，则更新α = x，node.next = subnode
若α ≥ β，则break循环
返回α
如果当前结点是MIN结点，即flag == 'MIN'：
α = 传递值，β = 传递值
遍历每个子结点subnode
调用 alpha-beta(subnode, a, β, 'MAX', depth+1)，得到返回值x
若x < β，则更新β = x，node.next = subnode
若α ≥ β，则break循环
返回β

五、 α-β算法的通用代码（最重要）

class Node:
    # 初始化数据成员
    def __init__(self,state,side):
        self.state = state      # 当前状态
        self.next = None        # 目标状态
    # 获取当前状态的全部子状态
    def get_substates(self,nextside):
        pass
    # 获取当前节点对应状态的目标价值
    def evaluate(self):
        pass
    # 检查是否是最佳状态或最坏状态
    def check(self):
        pass

def alpha_beta_cut(node:Node,alpha,beta,turn,depth,max_depth):
    flag = node.check()
    if flag == 最佳状态:
        return float('inf')
    elif flag == 最坏状态:
        return float('-inf')
    elif flag == 持平状态:
        return 0
    elif depth == max_depth:
        return node.evaluate()
    
    if turn == 'MAX':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates(turn):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MIN',depth+1,max_depth)
            if node_alpha < value:
                node_alpha = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_alpha

    if turn == 'MIN':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates(turn):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MAX',depth+1,max_depth)
            if node_beta > value:
                node_beta = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_beta

initial_state = [初始状态]
root = Node(initial_state)
nextstep = alpha_beta_cut(root,float('-inf'),float('inf'),'MAX',0,3)

六、案例分析：井字棋

假设AI先走x，人后走o

如果需要自定义对局双方是AI还是人，或者自定义AI先走还是人先走，可参考我的另一篇详细介绍井字棋实现的博客

http://t.csdnimg.cn/NeI7yhttp://t.csdnimg.cn/NeI7y

'''
棋盘设置：
0 1 2
3 4 5
6 7 8
'''

import math

class Node:
    def __init__(self,state):
        self.state = state
        self.next = None
    
    def check(self):
        # 检查行
        for i in range(0, 9, 3):
            if self.state[i] == self.state[i + 1] == self.state[i + 2] and self.state[i] != '_':
                return self.state[i]
        # 检查列
        for i in range(0, 3, 1):
            if self.state[i] == self.state[i + 3] == self.state[i + 6] and self.state[i] != '_':
                return self.state[i]
        # 检查对角线
        if self.state[0] == self.state[4] == self.state[8] and self.state[0] != '_':
            return state[0]
        if self.state[2] == self.state[4] == self.state[6] and self.state[2] != '_':
            return self.state[2]
        # 检查平局
        if '_' not in self.state:
            return 'Draw'
        return 'Continue'

    def evaluate(self):
        num_Xwin,num_Owin = 0,0
        #判定行
        for i in range(0,9,3):
            row = self.state[i:i+3]
            if 'o' not in row:
                num_Xwin += 1
            if 'x' not in row:
                num_Owin += 1
        #判定列
        for i in range(0,3):
            col = [self.state[i],self.state[i+3],self.state[i+6]]
            if 'o' not in col:
                num_Xwin += 1
            if 'x' not in col:
                num_Owin += 1
        #判断对角线
        diag1 = [self.state[0],self.state[4],self.state[8]]
        diag2 = [self.state[2],self.state[4],self.state[6]]
        if 'o' not in diag1:
            num_Xwin += 1
        if 'o' not in diag2:
            num_Xwin += 1 
        if 'x' not in diag1:
            num_Owin += 1
        if 'x' not in diag2:
            num_Owin += 1

        return num_Xwin - num_Owin 
    
    def get_substates(self,player):
        substates = []
        for i in range(9):
            if self.state[i] == '_':
                substate = list(self.state)
                substate[i] = player
                substates.append(substate)
        return substates
    
def alpha_beta_cut(node:Node,alpha,beta,type,depth,max_depth):
    if node.check() == 'x':
        return float('inf')
    if node.check() == 'o':
        return float('-inf')

    if depth == max_depth:
        return node.evaluate()
    
    if type == 'MAX':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates('x'):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MIN',depth+1,max_depth)
            if node_alpha < value:
                node_alpha = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_alpha

    if type == 'MIN':
        node_alpha,node_beta = alpha,beta
        for substate in node.get_substates('o'):
            subnode = Node(substate)
            value = alpha_beta_cut(subnode,node_alpha,node_beta,'MAX',depth+1,max_depth)
            if node_beta > value:
                node_beta = value
                node.next = substate
            if node_alpha >= node_beta:
                break
        return node_beta

def Print(state):
    for i in range(0,9,3):
        print(state[i],state[i+1],state[i+2])


state = ['_'] * 9
root = Node(state)
player = 'AI'
while 1:
    flag = root.check()
    if flag == 'Draw':
        print('平局')
        break
    elif flag == 'x':
        print('x获胜')
        break
    elif flag == 'o':
        print('o获胜')
        break
    elif flag == 'Continue':
        if player == 'HUMAN':
            index = int(input('HUMAN走棋，请输入你要下的位置：'))
            root.state[index] = 'o'
            Print(root.state)
            player = 'AI'
            continue
        if player == 'AI':
            print("AI走棋：")
            alpha_beta_cut(root,float('-inf'),float('inf'),'MAX',0,3)
            root.state = root.next
            Print(root.state)
            player = 'HUMAN'
            continue