统计基础（十一）逻辑回归与无参数回归

𝐋𝐨𝐠𝐢𝐬𝐭𝐢𝐜 𝐑𝐞𝐠𝐫𝐞𝐬𝐬𝐢𝐨𝐧 and Non-parametric Regression

1.知识点回顾

1.1 F测试

F测试有两种类型:

• 整体F检验——检验模型的有用性
• 部分F检验——检验线性约束
  

1.2多项R^2和多项R

R^2的正平方根等于r。与r不同的是，r可以取正值也可以取负值，r可以从0变化到1。R的值越接近1，自变量与因变量之间的线性关系越大。
▪R = 1表明预测是完全正确的。
▪R = 0表明自变量的线性组合不优于因变量的固定均值。

1.3 anova表

2.线性概率模型LPM

• 到目前为止，我们一直假设因变量是连续的(例如数量、价格等)。
• 然而，许多选择不能用连续变量来衡量。如:上不上大学;买房子或租房子;批准或不批准贷款申请;投不投工党等。
• 我们想要解释为什么做出这样的选择，哪些因素进入了决策过程，以及每个因素对结果的影响有多大。有时我们想预测这样的选择。
• 这样的选择导致模型中因变量Y在本质上是二元的(即等于0或1)。
• 在Y连续的模型中，我们的目标是在给定回归变量值的情况下估计其预期值或平均值;例如，我们想要E(Y | X1, X2，…，Xk)，其中X可以是定性的或定量的。
• 在Y为二进制的模型中，我们的目标是估计发生某事的概率;即P(Y = 1 | X1, X2，…，Xk)。因此，二元响应回归模型通常被称为概率模型。

▪我们首先考虑二元响应回归模型。有三种方法来开发一个二进制响应变量的概率模型:

• 线性概率模型(LPM)
• logit模型

2.2 线性概率模型(LPM)

▪考虑$Y_i={\beta }_0+{\beta }_1{X}_1+{\epsilon }_i$

• X =家庭收入
• 有房子的家庭Yi = 1，没有房子的家庭Yi = 0
• ε是一个随机误差，E(ε|X) = 0
  ▪由于因变量模型的二元性质(1)被称为线性概率模型(LPM)
  ▪令Pi 为 Yi = 1的概率，(1−Pi) 为 Yi = 0的概率。
  ▪因此，Yi遵循$E(Y_i)=P_i=P(Y_i=1)$的伯努利概率分布

Non-normality的随机误差ε𝐢

▪假设εi正态分布是对于LPMS是站不住脚的，像Yi的随机误差只有两个值
▪如果我们将模型改写为:εi = Yi -β0 - β1xi，则εi的概率分布为

因此，不能假定εi是正态分布的。相反，它们遵循伯努利分布。
▪不履行正态性假设有那么重要吗?

• 我们知道OLS点估计仍然是无偏的。
• 当样本容量无限增加时，OLS估计量趋向于正态分布
• 因此，在大样本中，LPM的统计推断将在正态假设下遵循通常的OLS程序

扰动的异方差

▪在LPM中，随机误差是同方差的，这已经不能再维持下去了。
▪误差项(服从伯努利分布)的方差为:$Var({\epsilon }_i)=P_i(1-P_i)$
▪自$P_i=E(Y_i|X_i)={\beta }_0+{\beta }_1{X}_i$,ε的方差我最终取决于X的值,因此并非同方差的:
$Var({\epsilon }_i)=P_i(1-P_i)=({\beta }_0+{\beta }_1{x}_i)(1-{\beta }_0-{\beta }_1{x}_i)$
▪因此，OLS估计器是无偏的，但效率不高

不履行的𝟎≤𝐄(𝐘𝐢|𝐗𝐢)≤𝟏

▪由于𝐄(𝐘𝐢|𝐗𝐢)在线性概率模型中测量给定X发生的事件Y的条件概率，它必须介于0和1之间，包括任何概率。
▪然而,Yi没有保证,估计的𝐄(𝐘𝐢|𝐗𝐢),一定会履行这个限制,这是真正的问题。
▪这是因为OLS不考虑限制𝟎≤𝐄(𝐘𝐢|𝐗𝐢)≤𝟏。

LPM的替代

▪LPM有几个问题:

• 指数εi非正态(不重要，如果样本大)
• 拟源i的异方差(可通过GLS减轻)
• Yi可能性范围超过0 - 1(可以调整拟合值)
  ▪LPM的根本问题是它不是很有吸引力，因为它假设Pi = E(y = 1|x)随X线性增长，即X的边际效应始终保持不变。也就是说，对于X的大值和低值，给定X的增加会导致Pi的相同变化。不现实!

▪我们需要一个有2个特征的概率模型:

• 随着Xi的增加，Pi = E(y = 1|x)会增加，但不会超出0-1区间。
• Pi和Xi的关系是非线性的。
  ▪在几何上，我们想要如下图所示(下一个图):
• 概率在0和1之间，随X非线性变化
• 类似于随机变量的累积分布函数(CDF)
  ▪但是——哪个CDF?Logistic (logit模型)或normal (probit模型)。
  

3.事件的概率

3.1 odds

概率用来表示事件发生的可能性，并表示为成功(s)与失败(f)的比率，反之亦然。

例子
一个首饰盒内有5颗白珍珠，2只金戒指和6只银戒指。从首饰盒里取出一颗白珍珠的几率有多大?
Odds(白珍珠)= 5/8或5:8
所以，事件发生的概率是5而不发生的概率是8。

3.2 odds ratio

一个事件的比值比(OR)比较第二个事件发生时的条件概率与第二个事件不发生时的条件概率;也就是说,

3.3 probability和odds

probability和odds不是一回事。它们包含相同的信息，但表达方式不同。
probability和odds可以用以下公式进行互换:
$$Odds=probability/(1-probability)$$
所以odds是两个互补probability的比值。
$$Probability=odds/(1+odds)$$
当probability为[0,1]时，odds为[0，∞)。

• 0的probability等于0的odds。
• 0.5的probability和1的odds一样。
• 0到0.5之间的probability等于小于1的odds。
• 随着probability从0。5增加到1，odds从1增加到∞。
• 高odds对应高probability，低odds对应低probability。

3.4二元因变量

回想一下线性概率模型，可以写成
$$P(Y=1|X)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_{k}Xk$$
▪线性概率模型的一个缺点是预测值不局限于0和1之间
▪另一种方法是将概率建模为函数F:
$$P(Y=1|X)=F({\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_{k}Xk)$$

• F(.)被称为转换。让z = β0 + β1X1+ β2X2 + βkXk它是一个(非线性)函数，具有以下两个良好特性:
  – i. 0 < F(z) < 1对于所有的z值
  – ii. F(z)在z方向上增加。

4.Logit模型/ logistic回归模型

▪F(z)的选择之一是logistic函数，它是一个标准logistic随机变量的cdf。
$$F(z)=\frac{exp(z)}{1+exp(z)}=\Lambda (z)$$

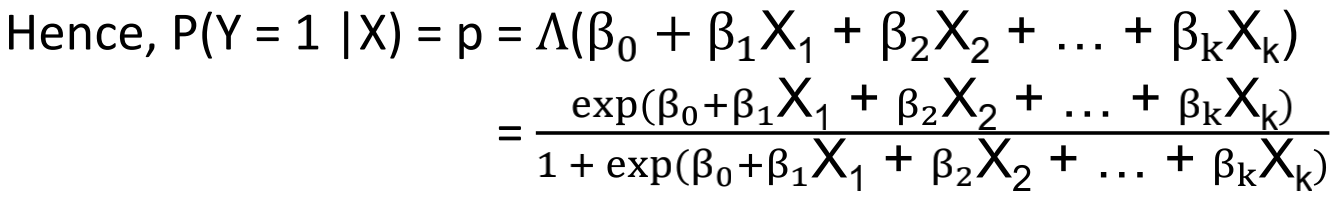
▪在logistic回归中，logistic变换的概率(简称logit)作为因变量;也就是说,
$ln(odds)=ln(p/(1-p))={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\dots +{\beta }_k{X}_k+\epsilon$
▪方程的左边称为“对数函数”或“对数概率”，即概率的对数。
$p=\frac{odds}{1+odds}$ 和 $odds=\frac{p}{1-p}$