1、数学期望(先判断是否存在——绝对收敛)
离散型随机变量:分布律(随机变量的取值——对应的概率)

连续型随机变量:先离散化后取极限,利用微积分办法推导

随机变量函数


2、性质

3、方差——衡量随机变量的取值与其均值之间的偏离程度

对方差开平方——标准差

方差 = 均方值 - 均值的平方
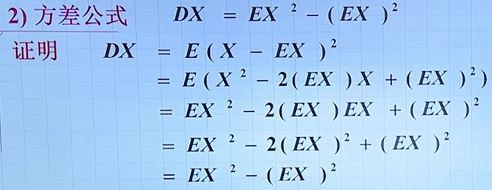
在实际的例子中,如果均值相等,则需要对比方差,方差越小越好。

注意:上面基本性质的证明都是从基本定义出发,慢慢展开计算。
——学习自中国大学生慕课MOOC《概率论与数理统计》- 北京交通大学理学院
1、数学期望(先判断是否存在——绝对收敛)
离散型随机变量:分布律(随机变量的取值——对应的概率)

连续型随机变量:先离散化后取极限,利用微积分办法推导

随机变量函数


2、性质

3、方差——衡量随机变量的取值与其均值之间的偏离程度

对方差开平方——标准差

方差 = 均方值 - 均值的平方
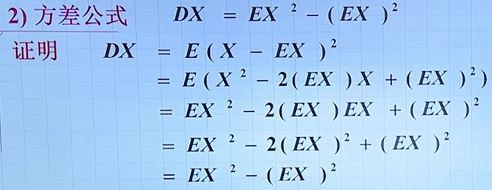
在实际的例子中,如果均值相等,则需要对比方差,方差越小越好。

注意:上面基本性质的证明都是从基本定义出发,慢慢展开计算。
——学习自中国大学生慕课MOOC《概率论与数理统计》- 北京交通大学理学院
 3万+
3万+
 201
201
 4414
4414
 1287
1287

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


