对称、群论与魔术（四）——空白扑克卡片的对称性研究

最新推荐文章于 2024-05-06 20:24:29 发布

MatheMagician

最新推荐文章于 2024-05-06 20:24:29 发布

阅读量924

点赞数

文章标签：人工智能 color microsoft 编程语言 asm

本文链接：https://blog.csdn.net/magic2728/article/details/124507081

版权

早点关注我，精彩不迷路！

在前面的文章中，我们从描述对称的困难到提出对称群的概念，以及拓展到群这一数学结构的多种应用，最后有回到几何对称的本源上。相关内容请戳：

对称、群论与魔术（三）——常见的几何对称性简介

对称、群论与魔术（二）——用群来描述对称性

对称、群论与魔术（一）——对称性本质探索

今天，我们继续聊如何用群的语言来描述对称，研究对象便是我们大家都熟悉的扑克牌。比如一个基本的问题是：

扑克牌是对称的吗？这样的对称有没有设计上的考虑？

我先说结论：扑克牌的对称性，每一张都不一样，这一切拼合在一起，最后到呈现在我们手中的扑克牌，都是精良的设计结果。

接着我们就还原一下从白卡片到手里真实扑克牌的演化过程，窥探其中对称性的变化以及从比较中发现设计之妙。

空白正方形卡片有怎样的对称性？

首先我们想象一下，如果扑克牌没有印刷以前，最开始是一个两面全白（或透明）的正方形卡片。我们可以看到，该对象沿着中心点任意旋转1, 2, 3个90度都可以保持自身不变，4个90度则真的恢复原状。同时，该正方形还可以翻转，看起来有水平，竖直和左右45度角4条翻转对称轴。该操作自身的性质便和Reverse一样，具有两次恢复自身的性质。如是，看起来加上自身，一共有8个对称操作和对应结果。但是，我们只需要旋转90度r以及水平翻转f这两个生成元，就可以构造出全部的操作：

e, r, r ^ 2, r ^ 3, f, rf, r ^ 2f, r ^ 3f

将这些操作和它们的结果画在图上，如图所示。

图1 透明正方形的全部对称操作示意图

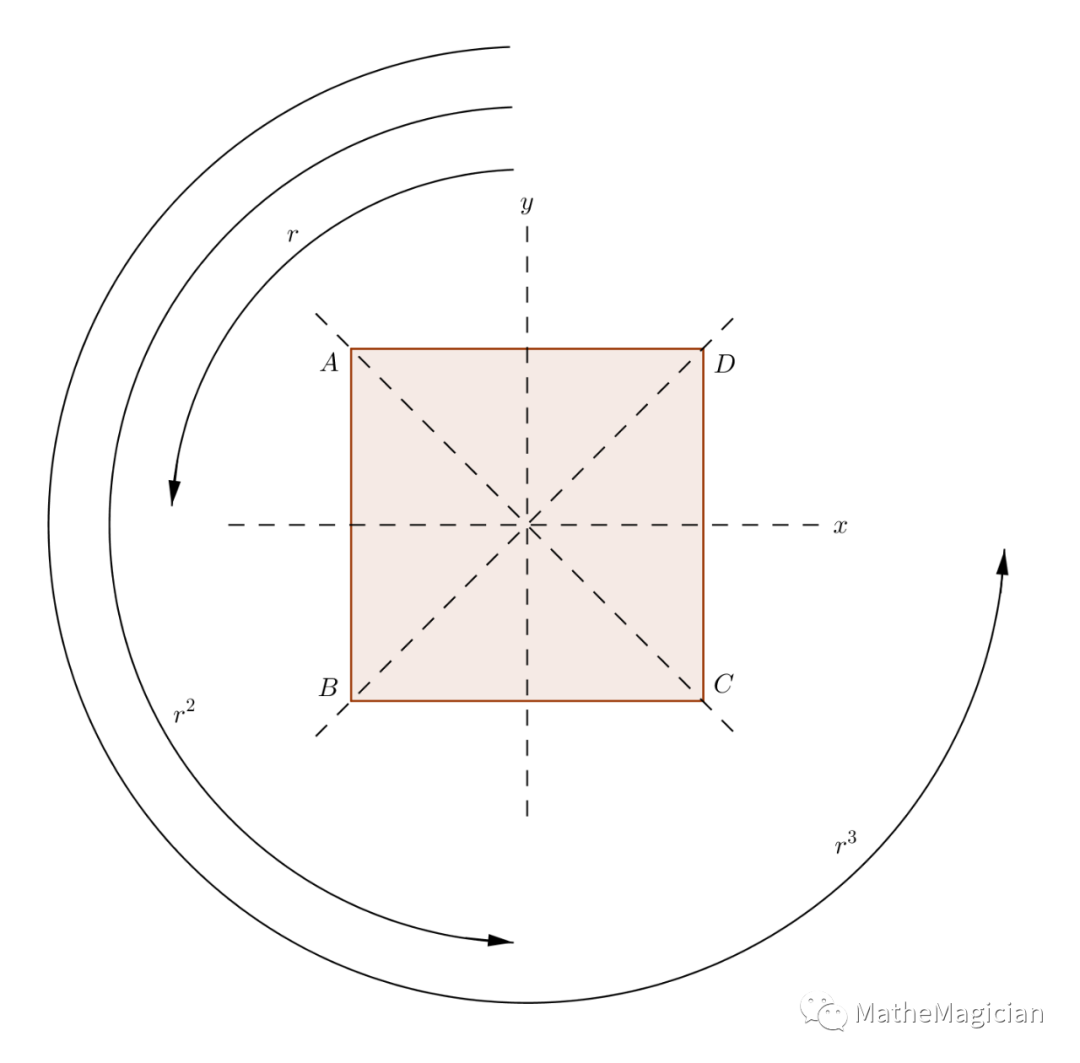
在图中可以观察到：rfrf = e，这一性质是在几何变换时候可以总结观察到的，也可以把这些操作用排列描述以后理论推导而来，总之着绝不是数学家瞎杜撰的。这一点大家拿一张扑克牌比如黑桃9转一下，翻一下，重复两次，看看是不是恢复到自己了？至于为什么要选黑桃9而不能选方块4之类的，我们后面马上聊到。

因此，这个透明正方形模型的不变操作集合，可以由基本操作来全部生成，而任意正多边形也都有类似的性质，我们统一把他们叫二面体群（dihedral group），从生成角度，记作：

Dn = <(r, f) | r ^ n = e, f ^ 2 = e, rfrf =e>

美妙的是，不管这是个正几边形，对应的Dn群都有一样的性质rfrf =e，这就是源于对对称和旋转这两个几何变换本质性质的总结，所以这仍然是一个数学模型，并非空洞无实际的数学理论。

其中正方形是n = 4的情形，其他三角形等以此类推。下面展示一下他们的Cayley Diagram，表达的是该群内所有元素以及相互之间的转换关系：

图2 Dn二面体群的Cayley Diagram

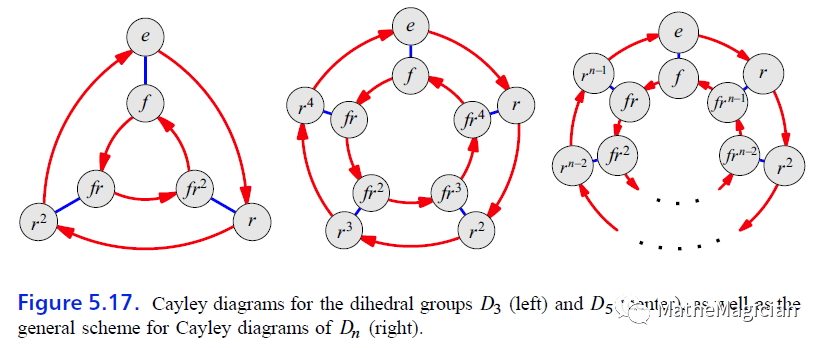
这个世界一定是先有了长得像三角形，正方形的东西，才逐步抽象出这些几何对象，进而抽象出里面这些对称性质等等的。而这些东西怎么来的？那一定是一个基本元素进行了物理上等效的那些几何变换得到的。我想这绝对是上帝的设计，因为这些内在数学结构的同构在太多地方都被人类发现了蛛丝马迹，人类一代代究其一生，就想搞明白上帝的逻辑。

插一句，我们对实际物体到几何体的抽象，和其他所有数学领域比如从给相似对象计数到离散可数的自然数的抽象，分蛋糕的分数抽象，还有对圆，三角函数，二次方程的根引发的实数的抽象，以及对无限累加和细分的极限运算的抽象等等，全都是类似的。这其中本身的数学模型在建立之初有着抓住重点矛盾的想法，略去了一些细节，然后方便地在数学世界里逻辑推演以后，如果你发现不符合实际，甚至在现实中产生了笑话（比如一个经典笑话就是，一个数学家拿着只够半面墙的半桶油漆涂满了所有有理点，油漆却一点不少；还有拓扑学家分不清甜甜圈和咖啡杯等等）。无论是自嘲还是沾沾自喜，这完全都不是批判数学无用论的论据。在数学建模中，本就有大量因为假设而导致结论不可用的情况，这些最经典最广泛的数学内容因其范围广，自然特异性下降。而数学框架内的研究更是本就是一门思维游戏，美学和艺术是其根源价值，至于在工程上的使用，本是附属品罢了。

到此，我们才算放心地研究清楚了两面等同的正n边形对称性的描述。不过反过来想，是因为正n边形长这样，两面相同，才有这些操作下真实验证成立的物理性质，进而总结出全部对称性。反过来，群是可以任意构造的，每个规定好生成元，运算法则满足群定义的群都成立，但是却不一定都找得到直接的实例，也却有可能有很多例子与其同构。这就是数学的魅力，有的没的对象，发明一套共同的语言来描述，干净地解决问题。

空白长方形卡片有怎样的对称性？

继续看，如果这张牌如真的牌一样，是长方形呢？此时就会由D4群退化到一个D2群，看起来，这个长方形和一个两头都有方向的平面箭头是同构的，甚至操作都一样，那就是翻转或旋转180度。其实可以虚构一个所谓的正两边形，把长方形也许可以看作一个胖胖的正二边形吧，或者干错就是一条线段。

图3 有D2群对称性的箭头图案和与其同构的长方形，线段

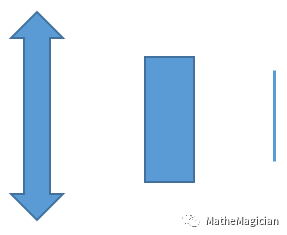
于是，拓扑学家分不清咖啡杯和甜甜圈的故事便有了升级版：群论专家分不清双向箭头，长方形（以及其对偶图形，菱形），线段和直线。

另外，其实菱形的对称性也和D2同构，你可以看菱形是长方形边到顶点变换的对偶图形就明白了。特别地，这种群有个名字，叫Klein-4 group，同构于D2群，一共有4种可能形态。

正反有别的长方形卡片有怎样的对称性？

好了，现在，扑克牌开始印刷了。显然，其天然就要承担隐蔽性，持牌的玩家和对家恰好看到牌的两面。因此，正常正多边形的透明性或者两面相同性是扑克牌不需要的。所以，f操作在真实的扑克牌上如果考虑到正反面图案的区别，也就不再满足对称性。纯粹是因为翻过来以后，所有的像素点都变了，看上去已经不再是刚才的牌，那自然没有翻转不变性了。而只有在没有印刷时候，所有像素点从两面上看过去没有区别才行。此时，该图案的对称操作集合的描述退化成一个循环群（cyclic group）：

Cn = {(r, f) | r ^ n = e}

当然，我们默认背面图案也是有C2对称性的，不然因为背面的原因，这个C2对称性也会一同消失掉。像Bicycle，Tallyho等牌背都是遵循中心对称的（Tallyho有细微差别，但很不明显），而国产的姚记有的有有的没有，钓鱼则一般就没有了，体现了国内这些厂家无论是从牌的品质，还是设计上的粗糙性。

正方形对应C4，而真实的扑克牌是长方形的，对应C2。在前面讲到《奇偶性与魔术（一）——奇偶性的数学本质》中曾经提到，奇数偶数两个子数集加上加法就构成一个C2群，当然你也可以说它与D1同构。但是为了尊重C一般源于类似旋转的操作，D代表翻转操作，我们不会这么叫，这只是习惯罢了，结构上并没有区别。而和Cn群同构的还有前后两面不同，不可翻折的正多边形的对称性，时钟表盘的旋转结果，整数在模加法上的运算；以及在《序列周期性与魔术（一）——数学里的函数周期性》中我们还提到了它也是描述扑克牌叠在仅二切操作下的全集。等等等等，万事万物都源自数学，都适合用数学来描述，总结。

本质上Cn群和Dn群与物理或几何上的旋转，翻折并没有任何关系，只不过这些操作是这些群在物理世界最典型甚至是起源性的现象，于是习惯性地以此来命名罢了。

特别的，C2群所描述的对称性一般地就是我们学过的中心对称，而D1群所描述的可以看作是我们讲的平面轴对称，三维空间面对称，甚至n维空间的(n – 1)维对称。注意了，有人把平面轴对称也当成一种沿着对称轴的旋转180度的空间旋转对称，这其实不对。那个不是真正的轴对称，是三维空间内的旋转对称，只不过在二维平面内刚好等价于对应轴的轴对称的结果罢了。但是，除了函数图像上那种f(a - x) = f(a + x)的轴对称，在空间上势必需要进行翻转的对折重合，也只有这种f操作才真的翻一下就能实现，不然那种只左右交换顶点，不翻面的变换，实际对象是做不到的。除非是三维空间内手套从内侧翻到外侧而且内外没有区别的这种物理变换，但这玩意在二维的纸面并不存在。所以，这些Cn群的对象虽然还存在像函数变换那样的对称轴 x = a，满足f(a - x) = f(a + x)，的确成立，但是，由于其是刚体，在平面内怎么平移旋转都做不了这种变换，因此只在Cn，但不在Dn的描述中成立，除非可以整个地翻转，两面等价。换句话说，这些群本身是为几何图形可行的刚体变换内的对称变换来服务描述的，而这一项变换，看起来要经过形变，或者只能抽象地以想象的方式理解。或者再换句话讲，你的眼睛从左往右和反过来扫过整个图片得到的图像是完全相同的，可以说对眼睛扫描该图像这个对象，改变方向这个操作不影响结果的对称性存在，可它并不在该图形的刚体变换范围内存在，刚体变换这个操作不对称，不代表别的方式不对称。

除了做triumph魔术时候的疯子洗牌法，我们整理扑克牌的时候都是朝一面整理的，本质上是在消除这一面不对称带来区别的影响，能够整体完成不让人看或看牌正面信息的局部观察结果（背面都一样，没有信息）。反过来，如果你印了几张字字或者背背的道具牌，打破了这个常规，往往就会产生意想不到的效果，这也是反向利用科学原理变魔术的方法。

另外，因为扑克牌是只有C2对称性的长方形，所以它不能像狼人杀牌那样随意旋转还能够互相码齐在一起，因为只有C4才有90度任意旋转的对称性，那个要求正方形。你看，就码齐这一点来讲，其实扑克牌可以算D2，需要小心翼翼别转90度以至于码不齐，我们整理扑克牌需要矩形的长短边对齐，其实就是使得在C2对称的范围内，消除不对称性，去消除这个90度旋转的自由度，码齐以后，每张牌的呈现应该和其摆放无关了。这就是不变性带来的好处，很难想象只有一个牌角有字的牌得有多难整理。而正方形的狼人杀牌可以算真正的C4，不过毕竟不是D4，还是有正反之分的，不能真的翻转不变。你看，对称性也是就某种特性来说的，不然，你进行了操作，总有某些东西是变的，不可能全都不变，这便是变与不变的相对性。至于为什么要长方形，而放弃了正方形码牌时候好码，在对应的也在4个脚上印上全等形，这样就再也不用担心长短不对齐了呢？我想是因为折中考虑了长方形牌更容易叠成一叠的时候拨开看到牌角，好拿进拿出吧，而狼人杀就一张，不太需要，从这个意义上讲，似乎德州扑克也可以做成正方形的来玩，还方便洗牌了。

到目前为止，我们讨论的扑克牌还是一张只有背面没有正面的长方形卡片，是C2群，别急，我们下一篇来看看印上图案的扑克牌究竟有着怎样的对称性了。