部分内容转自http://blog.csdn.net/jinshengtao/article/details/18448355
一、特征值与特征向量的几何意义
1. 矩阵乘法
在介绍特征值与特征向量的几何意义之前,先介绍矩阵乘法的几何意义。
矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度的新向量。在这个变化过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某些向量只发生伸缩变换,不产生旋转效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
比如下面的矩阵,它对应的线性变换是下面的形式形式:
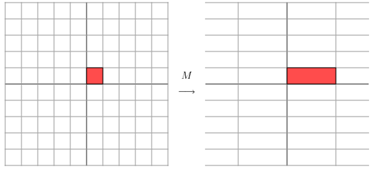
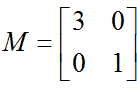
因为,这个矩阵乘以一个向量(x,y)的结果如下 :
1. 矩阵乘法
在介绍特征值与特征向量的几何意义之前,先介绍矩阵乘法的几何意义。
矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度的新向量。在这个变化过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某些向量只发生伸缩变换,不产生旋转效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
比如下面的矩阵,它对应的线性变换是下面的形式形式:

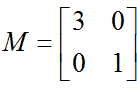
因为,这个矩阵乘以一个向量(x,y)的结果如下 :
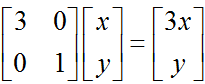
由于矩阵M是对称的,所以这个变换是一个对 x , y 轴的一个拉伸变换。【当M中元素值大于1时,是拉伸;当值小于1时,是缩短】
那么如果矩阵M不是对称的,比如下面的方程它所描述的变换为:
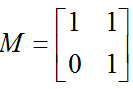
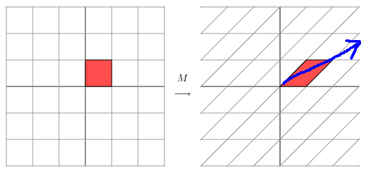
这其实是在平面上对一个轴进行的拉伸变换【如蓝色箭头所示】,在图中蓝色箭头是一个最主要的变化方向。变化方向可能有不止一个,但如果我们想要描述好一个变换,那我们就描述好这个变换主要的变化方向就好了。
2. 特征值分解与特征向量
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:
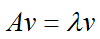
λ为特征向量 v 对应的特征值。特征值分解是将一个矩阵分解为如下形式:
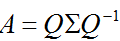
其中,Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角矩阵,每一个对角线元素就是一个特征值,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。也就是说矩阵A的信息可以由其特征值和特征向量表示。
对于矩阵为高维的情况下,那么这个矩阵就是高维空间下的一个线性变换。可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。
总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
二、奇异值分解
2. 特征值分解与特征向量
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:
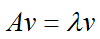
λ为特征向量 v 对应的特征值。特征值分解是将一个矩阵分解为如下形式:
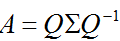
其中,Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角矩阵,每一个对角线元素就是一个特征值,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变化方向(从主要的变化到次要的变化排列)。也就是说矩阵A的信息可以由其特征值和特征向量表示。
对于矩阵为高维的情况下,那么这个矩阵就是高维空间下的一个线性变换。可以想象,这个变换也同样有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。
总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
二、奇异值分解
1. 奇异值
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有N个学生,每个学生有M科成绩,这样形成的一个N * M的矩阵就不可能是方阵,我们怎样才能描述这样普通的矩阵呢的重要特征呢?奇异值分解可以用来干这个事情,奇异值分解是一个能适用于任意的矩阵的一种分解的方法:
分解形式: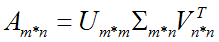
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有N个学生,每个学生有M科成绩,这样形成的一个N * M的矩阵就不可能是方阵,我们怎样才能描述这样普通的矩阵呢的重要特征呢?奇异值分解可以用来干这个事情,奇异值分解是一个能适用于任意的矩阵的一种分解的方法:
分解形式:
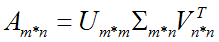
假设A是一个M * N的矩阵,那么得到的U是一个M * M的方阵(称为左奇异向量),Σ是一个M * N的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),VT(V的转置)是一个N * N的矩阵(称为右奇异向量)。
2. 奇异值分解的直观解释:
在矩阵M的奇异值分解中 M = UΣV*
·U的列(columns)组成一套对M的正交"输入"或"分析"的基向量。这些向量是MM*的特征向量。
·V的列(columns)组成一套对M的正交"输出"的基向量。这些向量是M*M的特征向量。
·Σ对角线上的元素是奇异值,可视为是在输入与输出间进行的标量的"膨胀控制"。这些是M*M及MM*的奇异值,并与U和V的行向量相对应
·U的列(columns)组成一套对M的正交"输入"或"分析"的基向量。这些向量是MM*的特征向量。
·V的列(columns)组成一套对M的正交"输出"的基向量。这些向量是M*M的特征向量。
·Σ对角线上的元素是奇异值,可视为是在输入与输出间进行的标量的"膨胀控制"。这些是M*M及MM*的奇异值,并与U和V的行向量相对应
3. 奇异值分解的几何意义
因为
U 和
V 向量都是单位化的向量, 我们知道
U的列向量
u1,...,
um组成了
Ku空间的一组
标准正交基。同样,
V的列向量
v1,...,
vn也组成了
Kv空间的一组标准正交基(根据向量空间的标准点积法则).
线性变换
T:
K →
K,把向量
Nx变换为
Mx。考虑到这些标准正交基,这个变换描述起来就很简单了:
T(
vi) =
σi ui, for
i = 1,...,min(
m,
n), 其中
σi 是对角阵Σ中的第
i个元素; 当
i > min(
m,
n)时,
T(
vi) = 0。
这样,SVD理论的几何意义就可以做如下的归纳:对于每一个线性映射
T:
K →
K,
T把
Kv的第
i个基向量映射为
Ku的第
i个
基向量的非负倍数,然后将余下的基向量映射为零向量。对照这些基向量,映射
T就可以表示为一个非负对角阵。
4. 奇异值与特征值
那么奇异值和特征值是怎么对应起来的呢?我们将一个矩阵A的转置乘以 A,并求特征值,则有下面的形式:
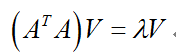
这里V就是上面的右奇异向量,另外还有:

这里的σ就是奇异值,u就是上面说的左奇异向量。
奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r( r远小于m、n )个的奇异值来近似描述矩阵,即部分奇异值分解:
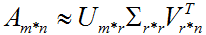
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。
5. 特征值分解与奇异值分解在信号处理中的体现:
在信号处理中经常碰到观测值的自相关矩阵,从物理意义上说,如果该观测值是由几个(如 K 个)相互统计独立的源信号线性混合而成,则该相关矩阵的秩或称维数就为 K,由这 K 个统计独立信号构成 K 维的线性空间,可由自相关矩阵最大 K 个特征值所对应的特征向量或观测值矩阵最大 K 个奇异值所对应的左奇异向量展成的子空间表示,通常称信号子空间,它的补空间称噪声子空间,两类子空间相互正交。理论上,由于噪声的存在,自相关矩阵是正定的,但实际应用时,由于样本数量有限,可能发生奇异,矩阵条件数无穷大,造成数值不稳定,并且自相关矩阵特征值是观测值矩阵奇异值的平方,数值动态范围大,因而子空间分析时常采用观测值矩阵奇异值分解,当然奇异值分解也可对奇异的自相关矩阵进行。在自相关矩阵正定时,特征值分解是奇异值分解的特例,且实现时相对简单些,实际中,常采用对角加载法保证自相关矩阵正定,对各特征子空间没有影响。在信号处理领域,两者都用于信号的特征分析,但两者的主要区别在于:奇异植分解主要用于数据矩阵,而特征植分解主要用于方型的相关矩阵 。
当信号协方差矩阵不是奇异矩阵时,则信号不相关或者部分相关。
三、奇异、秩与正定的基本概念
首先,看这个矩阵是不是方阵(即行数和列数相等的矩阵。若行数和列数不相等,那就谈不上奇异矩阵和非奇异矩阵)。 然后,再看此方阵的行列式
|A|是否等于0,若等于0,称矩阵A为奇异矩阵;若不等于0,称矩阵A为
非奇异矩阵
。 同时,由|A|≠0可知矩阵A可逆,这样可以得出另外一个重要结论:可逆矩阵
就是
非奇异矩阵
,非奇异矩阵也是可逆矩阵。 如果A为奇异矩阵,则AX=0有无穷解,AX=b有无穷解或者无解。如果A为
非奇异矩阵,则AX=0有且只有唯一零解,AX=b有唯一解。
一个方阵非奇异当且仅当它的行列式不为零。
一个方阵非奇异当且仅当它代表的线性变换是个自同构。
一个矩阵半正定当且仅当它的每个特征值大于或等于零。
一个矩阵正定当且仅当它的每个特征值都大于零。
一个方阵非奇异当且仅当它的行列式不为零。
一个方阵非奇异当且仅当它代表的线性变换是个自同构。
一个矩阵半正定当且仅当它的每个特征值大于或等于零。
一个矩阵正定当且仅当它的每个特征值都大于零。
非奇异矩阵还可以表示为若干个初等矩阵的乘积,证明中往往会被用到。
如果A(n×n)为奇异矩阵(singular matrix)<=> A的秩Rank(A)<n.
如果A(n×n)为非奇异矩阵(nonsingular matrix)<=> A满秩,Rank(A)=n.
Eviews软件中当样本容量太少或是当变量间存在完全相关性时会提示“near singular matrix”,意为“近奇异矩阵”。
如果A(n×n)为奇异矩阵(singular matrix)<=> A的秩Rank(A)<n.
如果A(n×n)为非奇异矩阵(nonsingular matrix)<=> A满秩,Rank(A)=n.
Eviews软件中当样本容量太少或是当变量间存在完全相关性时会提示“near singular matrix”,意为“近奇异矩阵”。





















 816
816

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








