使用K-Means聚类算法检测离群点

最新推荐文章于 2024-05-21 08:20:25 发布

吴下阿泽

最新推荐文章于 2024-05-21 08:20:25 发布

阅读量7.8k

点赞数 17

分类专栏：数据分析文章标签： python 聚类机器学习

本文链接：https://blog.csdn.net/maiyida123/article/details/117746461

版权

数据分析专栏收录该内容

9 篇文章

订阅专栏

1. 前言

数据集为电商真实订单数据经过处理后的RFM数据，来源为本人的文章《利用Python实现电商用户价值分层（RFM模型与基于RFM的K-Means聚类算法）》中第五小结聚类中的k_data。在该文章中并没有对离群点进行检测，所以在本文中，将使用K-Means检测其离群点。

2.代码

2.1 数据转换

载入数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei'] 
plt.rcParams['axes.unicode_minus'] = False  
plt.style.use('fivethirtyeight')
import warnings
warnings.filterwarnings("ignore")

data = pd.read_csv("rfm.csv", index_col = 'CustomerID')
data.head()

在这里插入图片描述

# 查看偏度、峰度
pd.DataFrame([i for i in zip(data.columns, data.skew(), data.kurt())], 
             columns=['特征', '偏度', '峰度'])

在这里插入图片描述

可见数据并不满足正态分布，所以接下来使用box-cox将其转换成正态分布

boxcox转换

# R中存在0值，进行box-cox转换时存在0值会将其转变成无穷大，所以将所有的值加上一个很小的数全部变成正数
data_bc = data.copy()
data_bc.R = data_bc.R + 0.0001

# boxcox转换
for i in data_bc.columns:  # 自动计算λ
    data_bc[i], _ = stats.boxcox(data_bc[i])

# 查看转换之后的偏度、峰度
pd.DataFrame([i for i in zip(data_bc.columns, data_bc.skew(), data_bc.kurt())], 
             columns=['特征', '偏度', '峰度'])

在这里插入图片描述

转换后的数据基本满足正态分布

数据标准化

from sklearn.preprocessing import scale
std_scale_data = scale(data_bc) # 标准化
std_data = pd.DataFrame(std_scale_data, columns = ['R', 'F', 'M'], index = data_bc.index)
std_data.head()

在这里插入图片描述
由于只有三个特征，所以无需将其降维，接下来将直接使用聚类算法决定类别

2.2 确定聚类类别

使用肘部法则确定聚类类别数

from sklearn.cluster import KMeans
# 选择K的范围 ，遍历每个值进行评估
inertia_list = []
for k in range(1,10):
    model = KMeans(n_clusters = k, max_iter = 500, random_state = 12)
    kmeans = model.fit(std_data)
    inertia_list.append(kmeans.inertia_)

# 绘图
fig,ax = plt.subplots(figsize=(8,6))    
ax.plot(range(1,10), inertia_list, '*-', linewidth=1)
ax.set_xlabel('k')
ax.set_ylabel("inertia_score") 
ax.set_title('inertia变化图')
plt.show()

在这里插入图片描述

从上图可见，曲线在2处有明显的拐点，所以选择2类比较合适

2.3 聚类

聚类

k = 2
threshold = 3  # 阈值选择3
model = KMeans(n_clusters = k, max_iter = 500)  # 分为k类
model.fit(std_data)  # 开始聚类
std_data['label'] = model.labels_ # 将聚类后的类别标签生成label列

计算相对距离

relative_distance = []
for i in range(k):  # 逐一处理
    distance = std_data.query("label == @i")[['R', 'F', 'M']] - model.cluster_centers_[i]  # 计算各点至簇中心点的距离
    absolute_distance = distance.apply(np.linalg.norm, axis = 1)  # 求出绝对距离
    relative_distance.append(absolute_distance / absolute_distance.median())  # 求相对距离并添加
    
std_data['relative_distance'] = pd.concat(relative_distance)  # 合并

筛选出离群点

std_data['outlier_3'] = std_data.relative_distance.apply(lambda x: 1 if x > threshold else 0)

查看离群点的数量

std_data['outlier_3'].value_counts()

在这里插入图片描述

一共检测出15个离群点

2.4 可视化

查看离群点的相对距离分布图

# 绘图查看离群点的相对距离
fig, ax = plt.subplots(figsize=(10,6))
colors = {0:'blue', 1:'red'}
ax.scatter(std_data.index, std_data.relative_distance, c=std_data.outlier_3.apply(lambda x: colors[x]))
ax.set_xlabel('客户ID')
ax.set_ylabel('相对距离')
plt.show()

在这里插入图片描述

可以看到阈值选择为3的时候，大于3的离群点都已被选出

查看离群点在rfm三个纬度的分布图

# 查看三维分布图
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12, 8), dpi=200)
ax = Axes3D(fig, rect = [0, 0, .95, 1], elev = 30, azim = -60)

ax1 = ax.scatter(std_data.query("outlier_3 == 0").R, std_data.query("outlier_3 == 0").F, 
                     std_data.query("outlier_3 == 0").M, edgecolor = 'k', color = 'r')
ax2 = ax.scatter(std_data.query("outlier_3 == 1").R, std_data.query("outlier_3 == 1").F, 
                     std_data.query("outlier_3 == 1").M, edgecolor = 'k', color = 'b')
ax.legend([ax1, ax2], ['正常点', '离群点'])
ax.invert_xaxis()
ax.set_xlabel('R')
ax.set_ylabel('F')
ax.set_zlabel('M')
ax.set_title('Outlier Scatter k={}'.format(threshold))
plt.show()

在这里插入图片描述

观察上图可以看到，检测出的离群点基本都分布在边缘

查看其R、F、M数据

data['outlier_3'] = std_data['outlier_3']
data.query("outlier_3 == 1")

在这里插入图片描述

可以看到，特征较极端的数据会被检测为离群值。

相对距离阈值k的选取直接影响了离群值的检测，我们查看k=2时的数据分布。

std_data['outlier_2'] = std_data.relative_distance.apply(lambda x: 1 if x > 2 else 0)

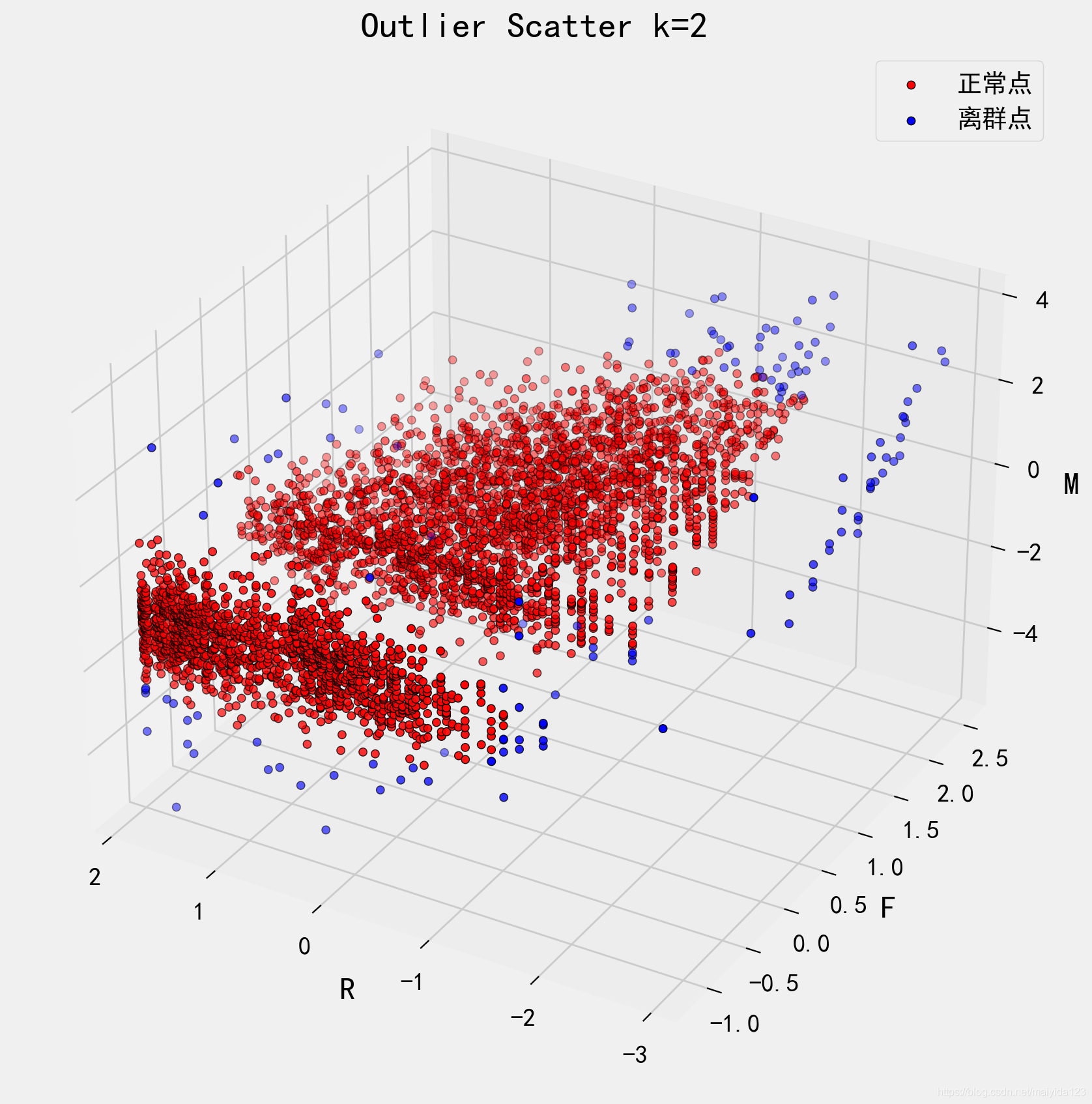
在这里插入图片描述

更多边缘的特征被检测为离群值

查看在k=2与3之间的值

# 查看在k=2与3之间的值前20个
data.query("outlier_3 ==0 & outlier_2 ==1").head(20)

在这里插入图片描述
可以看到，相对于k=3时检测出的离群值，k=2时的某些值显得并不那么“极端”，看起来并不符合业务逻辑。

所以k的选取尤为关键，至于如何选取k值，则需要依业务场景而论。

参考书籍：Python数据分析与挖掘实战