机器学习总结（lecture 10）算法：支持向量机SVM

lecture 10：支持向量机SVM

目录

1大间隔分类超平面

例如对平面2D这种情况，我们可以找到一条直线，能将正类和负类完全分开。但是，这样的直线通常不止一条，如下图所示。那么，下图中的三条分类线都能将数据分开，但是哪条线更好呢？

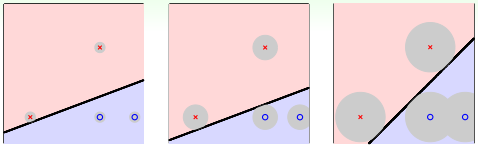
凭第一感觉，我们还是会选择第三条直线，感觉它的分类效果更好一些。那这又是为什么呢？

先给个简单解释，一般情况下，训练样本外的测量数据应该分布在训练样本附近，但与训练样本的位置有一些偏差。若要保证对未知的测量数据也能进行正确分类，最好让分类直线距离正类负类的点都有一定的距离。这样能让每个样本点附近的圆形区域是“安全”的。圆形区域越大，表示分类直线对测量数据误差的容忍性越高，越“安全”。

noise是造成overfitting的主要原因

• 上面我们用圆形区域表示分类线能够容忍多少误差，也就相当于计算点到直线的距离。距离越大，表示直线越“胖”，越能容忍误差；距离越小，表示直线越“瘦”，越不能容忍误差。
• 越胖越好

如何定义分类线有多胖，就是看距离分类线最近的点与分类线的距离，我们把它用margin表示。分类线由权重w决定，目的就是找到使margin最大时对应的w值。整体来说，我们的目标就是找到这样的分类线并满足下列条件：


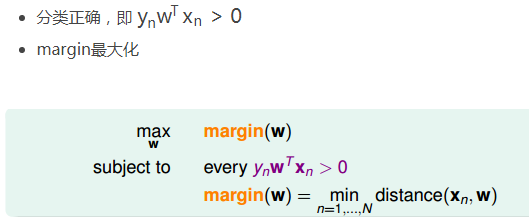
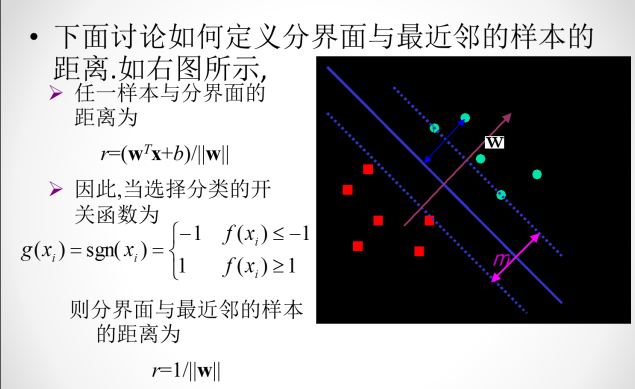
这样，目标形式就简化为：

2SVM在Linear Hard-Margin SVM

• 决定分类面的几个点称之为支持向量（Support Vector），这些点支撑着分类面。

SVM的一般求解方法是一个典型的二次规划问题，即Quadratic Programming（QP）。因为SVM的目标是关于w的二次函数，条件是关于w和b的一次函数，所以，它的求解过程还是比较容易的，可以使用一些软件（例如Matlab）自带的二次规划的库函数来求解。下图给出SVM与标准二次规划问题的参数对应关系：

这种方法称为Linear Hard-Margin SVM Algorithm。如果是非线性的，例如包含x的高阶项，那么可以使用特征转换的方法，先作zn=Φ(xn)的特征变换，从非线性的x域映射到线性的z域空间，再利用Linear Hard-Margin SVM Algorithm求解即可。

• 由于Large-Margin的限制，得到的dichotomies（二分法）个数减少（分开两类的直线数目），从而VC Dimension也减少了。VC Dimension减少降低了模型复杂度，提高了泛化能力。
• SVM 泛化能力很好

3对偶Dual SVM

• 对于非线性SVM，可以使用非线性变换将变量从x域转换到z域中。然后，在z域中，使用线性SVM解决问题即可。
• 使用SVM得到large-margin，减少了有效的VC Dimension，限制了模型复杂度
• 另一方面，使用特征转换，目的是让模型更复杂。
• 所以说，非线性SVM是把这两者目的结合起来，平衡这两者的关系。

特征转换下，求解QP问题在z域中的维度设为d+1，如果模型越复杂，则d+1越大，相应求解这个QP问题也变得很困难。当d无限大的时候，问题将会变得难以求解，那么有没有什么办法可以解决这个问题呢？一种方法就是使SVM的求解过程不依赖d

引入拉格朗日因子

下面，我们利用拉格朗日函数，把SVM构造成一个非条件问题：

经过推导，SVM对偶问题的解已经转化为无条件形式：

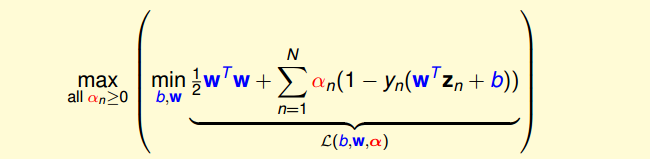
（1）其中，上式括号里面的是对拉格朗日函数L(b,w,α)计算最小值。那么根据梯度下降算法思想：最小值位置满足梯度为零。首先，令L(b,w,α)对参数b的梯度为零：

（2）这样，SVM表达式消去了b，问题化简了一些。然后，再根据最小值思想，令L(b,w,α)对参数w的梯度为零：

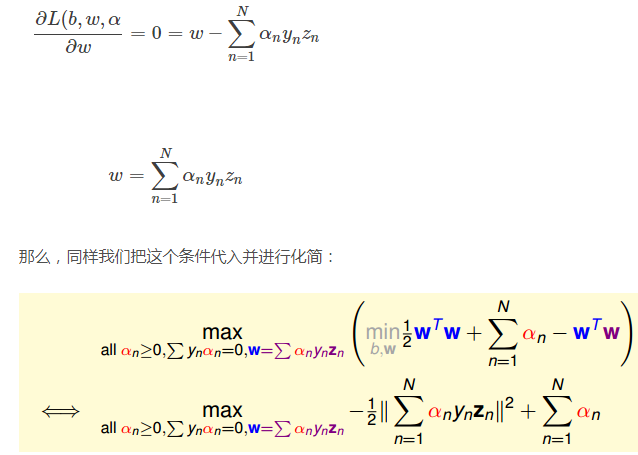
（3）这样，SVM表达式消去了w，问题更加简化了。这时候的条件有3个：

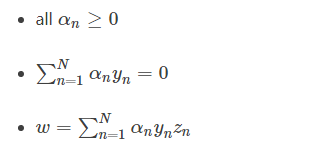
总结一下，SVM最佳化形式转化为只与αn有关：

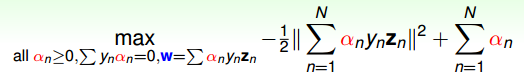
其中，满足最佳化的条件称之为Karush-Kuhn-Tucker(KKT)

4Solving Dual SVM

上面我们已经得到了dual SVM的简化版了，接下来，我们继续对它进行一些优化。首先，将max问题转化为min问题，再做一些条件整理和推导，得到：

显然，这是一个convex（凸）的QP问题，且有N个变量αn，限制条件有N+1个。则根据上一节课讲的QP解法，找到Q，p，A，c对应的值，用软件工具包进行求解即可。


这节课提出的Dual SVM的目的是为了避免计算过程中对d^的依赖，而只与N有关。但是，Dual SVM是否真的消除了对d^的依赖呢？其实并没有。因为在计算qn,m=ynymzTnzm的过程中，由z向量引入了d^，实际上复杂度已经隐藏在计算过程中了。所以，我们的目标并没有实现。

5Kernel SVM

5.1核技巧

d^的影响没有被消除

我们先来看一个简单的例子，对于二阶多项式转换，各种排列组合为：

这里提一下，为了简单起见，我们把x0=1包含进来，同时将二次项x1x2和x2x1也包含进来。转换之后再做内积并进行推导，得到：

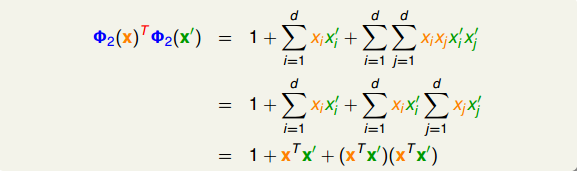
• 把特征转换和z空间计算内积这两个步骤合并起来，会简化计算

5.2多项式核、高斯核

我们刚刚通过一个特殊的二次多项式导出了相对应的kernel，其实二次多项式的kernel形式是多种的。例如，相应系数的放缩构成完全平方公式等。下面列举了几种常用的二次多项式kernel形式：

比较一下，第一种Φ2(x)（蓝色标记）和第三种Φ2(x)（绿色标记）从某种角度来说是一样的，因为都是二次转换，对应到同一个z空间。但是，它们系数不同，内积就会有差异，那么就代表有不同的距离，最终可能会得到不同的SVM margin。所以，系数不同，可能会得到不同的SVM分界线。通常情况下，第三种Φ2(x)（绿色标记）简单一些，更加常用。

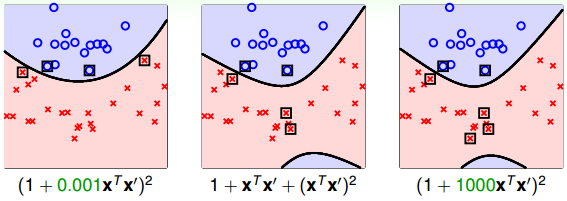
通过改变不同的系数，得到不同的SVM margin和SV，如何选择正确的kernel，非常重要。

所以，使用高阶的多项式kernel有两个优点

• 得到最大SVM margin，SV数量不会太多，分类面不会太复杂，防止过拟合，减少复杂度
• 计算过程避免了对d^的依赖，大大简化了计算量。

刚刚我们介绍的Q阶多项式kernel的阶数是有限的，即特征转换的d^是有限的。但是，如果是无限多维的转换Φ(x)，是否还能通过kernel的思想，来简化SVM的计算呢？答案是肯定的。

先举个例子，简单起见，假设原空间是一维的，只有一个特征x，我们构造一个kernel function为高斯函数：

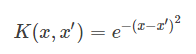
• 通过上式可以看出gSVM由n个高斯函数线性组合而成，其中n是SV（支持向量）的个数。
• 而且，每个高斯函数的中心都是对应的SV。通常我们也把高斯核函数称为径向基函数（Radial Basis Function，RBF）。

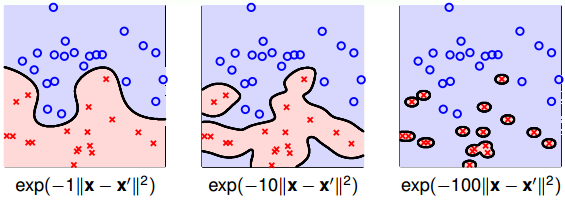
值得注意的是，缩放因子γ取值不同，会得到不同的高斯核函数，hyperplanes不同，分类效果也有很大的差异。举个例子，γ分别取1, 10, 100时对应的分类效果如下：

从图中可以看出，当γ比较小的时候，分类线比较光滑，当γ越来越大的时候，分类线变得越来越复杂和扭曲，直到最后，分类线变成一个个独立的小区域，像小岛一样将每个样本单独包起来了。为什么会出现这种区别呢？这是因为γ越大，其对应的高斯核函数越尖瘦，那么有限个高斯核函数的线性组合就比较离散，分类效果并不好。所以，SVM也会出现过拟合现象，γ的正确选择尤为重要，不能太大。

6soft-margin SVM

我们之前讲的这些方法都是Hard-Margin SVM，即必须将所有的样本都分类正确才行。这往往需要更多更复杂的特征转换，甚至造成过拟合。

Soft-Margin SVM，目的是让分类错误的点越少越好，而不是必须将所有点分类正确，也就是允许有noise存在。这种做法很大程度上不会使模型过于复杂，不会造成过拟合，而且分类效果是令人满意的。

SVM同样可能会造成overfit。原因有两个，

• 一个是由于我们的SVM模型（即kernel）过于复杂，转换的维度太多，过于powerful了；
• 另外一个是由于我们坚持要将所有的样本都分类正确，即不允许错误存在，造成模型过于复杂

为了引入允许犯错误的点，我们将Hard-Margin SVM的目标和条件做一些结合和修正，转换为如下形式：


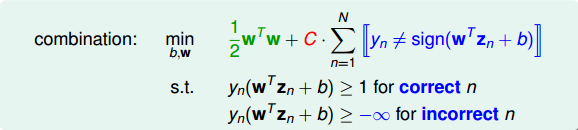
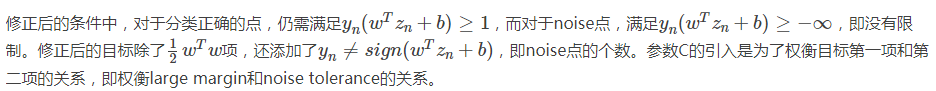
我们再对上述的条件做修正，将两个条件合并，得到：

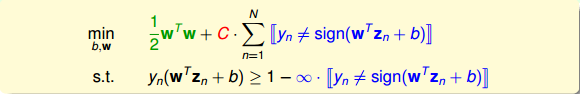
这个式子存在两个不足的地方。首先，最小化目标中第二项是非线性的，不满足QP的条件，所以无法使用dual或者kernel SVM来计算。然后，对于犯错误的点，有的离边界很近，即error小，而有的离边界很远，error很大，上式的条件和目标没有区分small error和large error。这种分类效果是不完美的。

为了改正这些不足，我们继续做如下修正：

• 其中，ξn表示每个点犯错误的程度，ξn=0，表示没有错误，ξn越大，表示错误越大，即点距离边界（负的）越大。
• 参数C表示尽可能选择宽边界和尽可能不要犯错两者之间的权衡，因为边界宽了，往往犯错误的点会增加。
• large C表示希望得到更少的分类错误，即不惜选择窄边界也要尽可能把更多点正确分类；
• small C表示希望得到更宽的边界，即不惜增加错误点个数也要选择更宽的分类边界。

6.1Soft-Margin SVM的对偶形式

因为引入了ξn，原始问题有两类条件，所以包含了两个拉格朗日因子αn和βn。拉格朗日函数可表示为如下形式：

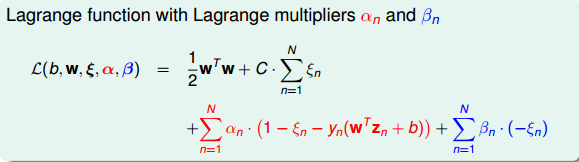
接下来，与前面做法一样，利用Lagrange dual problem，将Soft-Margin SVM问题转换为如下形式：






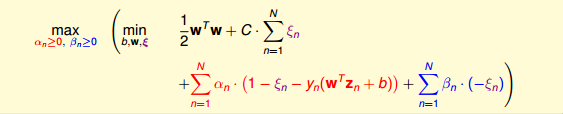
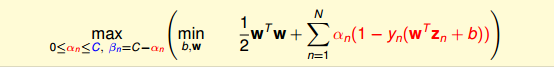
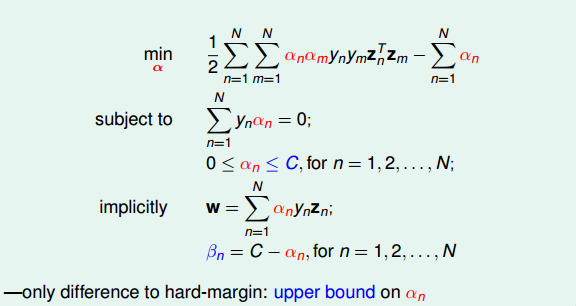
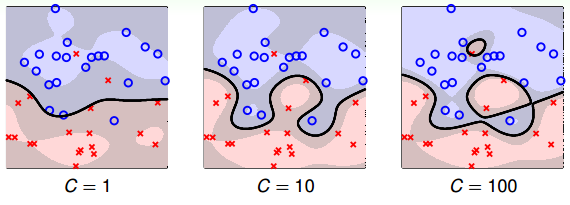
接下来，我们看看C取不同的值对margin的影响。例如，对于Soft-Margin Gaussian SVM，C分别取1，10，100时，相应的margin如下图所示：

• 从上图可以看出，C=1时，margin比较粗，但是分类错误的点也比较多
• 当C越来越大的时候，margin越来越细，分类错误的点也在减少。正如前面介绍的，C值反映了margin和分类正确的一个权衡。
• C越小，越倾向于得到粗的margin，宁可增加分类错误的点；
• C越大，越倾向于得到高的分类正确率，宁可margin很细。
• 我们发现，当C值很大的时候，虽然分类正确率提高，但很可能把noise也进行了处理，从而可能造成过拟合。
• 也就是说Soft-Margin Gaussian SVM同样可能会出现过拟合现象，所以参数(γ,C)的选择非常重要。

不同的(C,γ)组合，margin的差别很大。那么如何选择最好的(C,γ)等参数呢？最简单最好用的工具就是validation。V-Fold cross validation

• SVM关键在于选择核函数，确定松弛系数C和惩罚系数ξn。

7序列最小化优化SMO算法

sequential minimal optimization
参考博客：https://www.cnblogs.com/pinard/p/6111471.html