吴恩达Coursera深度学习（1-4）编程练习

最新推荐文章于 2024-10-06 16:03:34 发布

九方先生

最新推荐文章于 2024-10-06 16:03:34 发布

阅读量4.5k

点赞数 3

分类专栏： Coursera深度学习编程练习

本文链接：https://blog.csdn.net/malele4th/article/details/79381054

版权

Coursera深度学习编程练习专栏收录该内容

10 篇文章 4 订阅

订阅专栏

Class 1：神经网络和深度学习

Week 4：深层神经网络——编程练习

import numpy as np
import matplotlib.pyplot as plt
import h5py

# 1 下载数据集
def load_data():
    train_dataset    = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset     = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig  = np.array(test_dataset["test_set_x"][:])   # your test set features
    test_set_y_orig  = np.array(test_dataset["test_set_y"][:])   # your test set labels

    classes = np.array(test_dataset["list_classes"][:])          # the list of classes

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig  = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

# 2-1 初始化参数：2层
def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input  layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer

    Returns:
    parameters -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape   (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape   (n_y, 1)
    """ 
    np.random.seed(1)

    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros((n_y, 1))

    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters     

# 2-2 初始化参数：L层
def initialize_parameters_deep(layer_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the dimensions of each layer in our network

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    Wl -- weight matrix of shape (layer_dims[l], layer_dims[l-1])
                    bl -- bias vector of shape (layer_dims[l], 1)
    """   
    np.random.seed(1)
    parameters = {}
    L = len(layer_dims)            # number of layers in the network

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1])*0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))

        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))

    return parameters

# 3-1 激活函数：sigmoid
def sigmoid(Z):
    """
    Implements the sigmoid activation in numpy

    Arguments:
    Z -- numpy array of any shape

    Returns:
    A     -- output of sigmoid(z), same shape as Z
    cache -- returns Z as well, useful during backpropagation
    """ 
    A = 1/(1+np.exp(-Z))
    cache = Z
    return A, cache

# 3-2 激活函数：ReLU
def relu(Z):
    """
    Implement the ReLU function.

    Arguments:
    Z -- Output of the linear layer, of any shape

    Returns:
    A     -- Post activation parameter, of the same shape as Z
    cache -- a python dictionary containing "A" ; stored for computing  backward efficiently
    """
    A = np.maximum(0,Z)
    assert(A.shape == Z.shape)

    cache = Z 
    return A, cache

# 4-1 relu backward, 对激活函数计算后向传播
def relu_backward(dA, cache):
    """
    Implement the backward propagation for a single RELU unit.

    Arguments:
    dA    -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """

    Z  = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.

    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0
    assert (dZ.shape == Z.shape)
    return dZ

# 4-2 sigmoid backward 对激活函数计算后向传播
def sigmoid_backward(dA, cache):
    """
    Implement the backward propagation for a single SIGMOID unit.

    Arguments:
    dA    -- post-activation gradient, of any shape
    cache -- 'Z' where we store for computing backward propagation efficiently

    Returns:
    dZ -- Gradient of the cost with respect to Z
    """
    Z = cache
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)            # 感觉 dA = dZ * s * (1-s)

    assert (dZ.shape == Z.shape)
    return dZ

# 5-1 前向传播的线性部分
def linear_forward(A, W, b):
    """
    Implement the linear part of a layer's forward propagation.

    Arguments:
    A -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)

    Returns:
    Z     -- the input of the activation function, also called pre-activation parameter 
    cache -- a python dictionary containing "A", "W"，"b" ; stored for computing the backward efficiently
    """
    Z = np.dot(W,A) + b
    assert(Z.shape == (W.shape[0], A.shape[1]))
    cache = (A, W, b)
    return Z, cache

# 5-2 前向传播线性激活
def linear_activation_forward(A_prev, W, b, activation):
    """
    Implement the forward propagation for the LINEAR->ACTIVATION layer

    Arguments:
    A_prev -- activations from previous layer (or input data): (size of previous layer, number of examples)
    W -- weights matrix: numpy array of shape (size of current layer, size of previous layer)
    b -- bias vector, numpy array of shape (size of the current layer, 1)
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    A     -- the output of the activation function, also called the post-activation value 
    cache -- a python dictionary containing "linear_cache" and "activation_cache";
             stored for computing the backward pass efficiently
    """

    if activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)

    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)

    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)  # linear_cache     包含: A_prev,W,b
                                              # activation_cache 包含：Z
    return A, cache   # cache 包含 A_prev, W, b, Z

# 5-3 L模型 前向传播
def L_model_forward(X, parameters):
    """
    Implement forward propagation for the [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID computation

    Arguments:
    X          -- data, numpy array of shape (input size, number of examples)
    parameters -- output of initialize_parameters_deep()

    Returns:
    AL     -- last post-activation value
    caches -- list of caches containing:
                every cache of linear_relu_forward() (there are L-1 of them, indexed from 0 to L-2)
                the cache of linear_sigmoid_forward() (there is one, indexed L-1)
    """
    caches = []
    A = X
    L = len(parameters) // 2      # number of layers in the neural network

    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    for l in range(1, L):
        A_prev = A 
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")
        caches.append(cache)

    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
    caches.append(cache)

    assert(AL.shape == (1,X.shape[1]))

    return AL, caches   # caches 包含每一层的 A_prev, W, b, Z

# 6 计算损失函数
def compute_cost(AL, Y):
    """
    Implement the cost function 

    Arguments:
    AL -- probability vector corresponding to your label predictions, shape (1, number of examples)
    Y  -- true "label" vector (for example: containing 0 if non-cat, 1 if cat), shape (1, number of examples)

    Returns:
    cost -- cross entropy cost
    """

    m = Y.shape[1]

    # Compute loss from AL and y.
    cost = (1./m) * (-np.dot(Y,np.log(AL).T) - np.dot(1-Y, np.log(1-AL).T))
    cost = np.squeeze(cost)   # To make sure your cost's shape is what we expect
    return cost

# 7-1 反向传播 线性部分
def linear_backward(dZ, cache):
    """
    Implement the linear portion of backward propagation for a single layer (layer l)

    Arguments:
    dZ    -- Gradient of the cost with respect to the linear output (of current layer l)
    cache -- tuple of values (A_prev, W, b) coming from the forward propagation in the current layer

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW      -- Gradient of the cost with respect to W (current layer l), same shape as W
    db      -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]

    dW = 1./m * np.dot(dZ,A_prev.T)
    db = 1./m * np.sum(dZ, axis = 1, keepdims = True)
    dA_prev = np.dot(W.T,dZ)

    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)

    return dA_prev, dW, db

# 7-2 反向传播： 线性激活
def linear_activation_backward(dA, cache, activation):
    """
    Implement the backward propagation for the LINEAR->ACTIVATION layer.

    Arguments:
    dA         -- post-activation gradient for current layer l 
    cache      -- tuple of values (linear_cache, activation_cache) we store for computing backward propagation efficiently
    activation -- the activation to be used in this layer, stored as a text string: "sigmoid" or "relu"

    Returns:
    dA_prev -- Gradient of the cost with respect to the activation (of the previous layer l-1), same shape as A_prev
    dW      -- Gradient of the cost with respect to W (current layer l), same shape as W
    db      -- Gradient of the cost with respect to b (current layer l), same shape as b
    """
    linear_cache, activation_cache = cache

    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    return dA_prev, dW, db

# 7-3 反向传播 L模型
def L_model_backward(AL, Y, caches):
    """
    Implement the backward propagation for the [LINEAR->RELU] * (L-1) -> LINEAR -> SIGMOID group

    Arguments:
    AL -- probability vector, output of the forward propagation (L_model_forward())
    Y -- true "label" vector (containing 0 if non-cat, 1 if cat)
    caches -- list of caches containing:
                every cache of linear_activation_forward() with "relu" (there are (L-1) or them, indexes from 0 to L-2)
                the cache of linear_activation_forward() with "sigmoid" (there is one, index L-1)

    Returns:
    grads -- A dictionary with the gradients
             grads["dA" + str(l)] = ... 
             grads["dW" + str(l)] = ...
             grads["db" + str(l)] = ... 
    """
    grads = {}
    L = len(caches)  # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL

    # Initializing the backpropagation
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
    current_cache = caches[L-1]
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")

    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, activation = "relu")
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp

    return grads

# 8、更新参数
def update_parameters(parameters, grads, learning_rate):
    """
    Update parameters using gradient descent

    Arguments:
    parameters -- python dictionary containing your parameters 
    grads      -- python dictionary containing your gradients, output of L_model_backward

    Returns:
    parameters -- python dictionary containing your updated parameters 
                  parameters["W" + str(l)] = ... 
                  parameters["b" + str(l)] = ...
    """

    L = len(parameters) // 2 # number of layers in the neural network

    # Update rule for each parameter. Use a for loop.
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]

    return parameters

# 9、预测新样本
def predict(X, y, parameters):
    """
    This function is used to predict the results of a  L-layer neural network.

    Arguments:
    X -- data set of examples you would like to label
    parameters -- parameters of the trained model

    Returns:
    p -- predictions for the given dataset X
    """

    m = X.shape[1]
    n = len(parameters) // 2 # number of layers in the neural network
    p = np.zeros((1,m))

    # Forward propagation
    probas, caches = L_model_forward(X, parameters)


    # convert probas to 0/1 predictions
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0

    print("Accuracy: "  + str(np.sum((p == y)/m)))    
    return p

# 10、打印错误标签的图像
def print_mislabeled_images(classes, X, y, p):
    """
    Plots images where predictions and truth were different.
    X -- dataset
    y -- true labels
    p -- predictions
    """
    a = p + y
    mislabeled_indices = np.asarray(np.where(a == 1))  # 返回错误的索引
    plt.rcParams['figure.figsize'] = (40.0, 40.0)      # set default size of plots
    num_images = len(mislabeled_indices[0])            # 识别错误的数量

    for i in range(num_images):
        index = mislabeled_indices[1][i]

        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
        plt.axis('off')
        plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8"))
    plt.show()

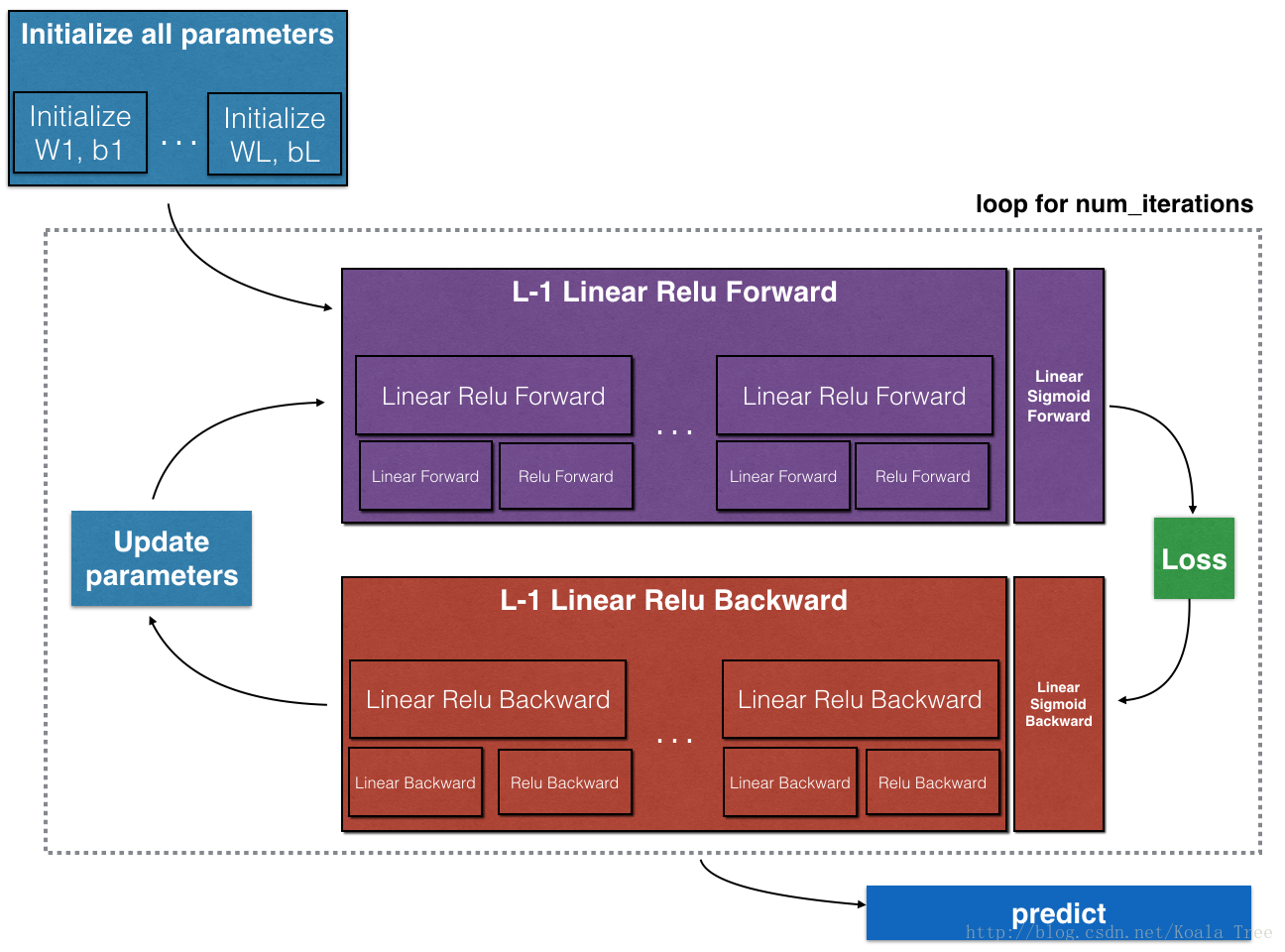
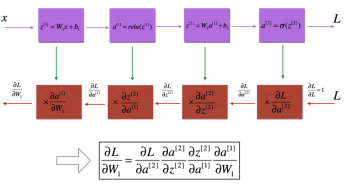
2、初始化模型参数及反向传播

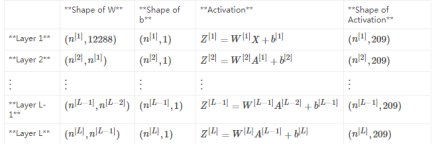
这里写图片描述

3、两层、L层神经网络模型

import time
import numpy as np 
import matplotlib.pyplot as plt 
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from testCases_v2 import *
from dnn_app_utils_v2 import *

plt.rcParams['figure.figsize'] = (5.0,4.0)      #设置 plots 的默认大小
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

np.random.seed(1)

# 1、数据集
train_x_orig, train_y, test_x_orig, test_y, classes = load_data()
num_px = train_x_orig.shape[1]
print(train_x_orig.shape, test_x_orig.shape)

'''
# 显示其中一张图片
index = 10
plt.imshow(train_x_orig[index])
plt.show()
print ("y = " + str(train_y[0,index]) +\
       ". It's a " + classes[train_y[0,index]].decode("utf-8") +  " picture.")
'''

# 重铺数据，并标准化
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T  
test_x_flatten  = test_x_orig.reshape(test_x_orig.shape[0], -1).T

train_x = train_x_flatten/255.
test_x  = test_x_flatten/255.
print(train_x.shape, test_x.shape)

# 2、两层神经网络
# 输出 w1 w2 b1 b2
def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
    np.random.seed(1)
    m = X.shape[1]
    (n_x, n_h, n_y) = layers_dims
    grads = {}
    costs = []

    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    b1 = parameters["b1"]
    b2 = parameters["b2"]

    for i in range(0, num_iterations):
        A1, cache1 = linear_activation_forward(X,  W1, b1, activation="relu")
        A2, cache2 = linear_activation_forward(A1, W2, b2, activation="sigmoid")

        cost = compute_cost(A2, Y)

        # 初始化反向传播
        dA2 = - (np.divide(Y, A2) - np.divide(1-Y, 1-A2))
        #dA2 = np.power(Y-A2,2) #代价函数升高

        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, activation="sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, activation="relu")

        grads["dW1"] = dW1
        grads["dW2"] = dW2
        grads["db1"] = db1
        grads["db2"] = db2

        parameters = update_parameters(parameters, grads, learning_rate)

        W1 = parameters["W1"]
        W2 = parameters["W2"]
        b1 = parameters["b1"]
        b2 = parameters["b2"]

        if print_cost and i%100==0:
            costs.append(cost)
            print("cost after iteration {}:{}".format(i, np.squeeze(cost)))

    plt.plot(np.squeeze(costs))
    plt.xlabel('iterations (per 100)')
    plt.ylabel('cost')
    plt.title("learning rate = " + str(learning_rate))
    plt.show()

    return parameters

# 3、L层神经网络
def L_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False):
    np.random.seed(1)
    costs = []
    parameters = initialize_parameters_deep(layers_dims)

    for i in range(0, num_iterations):
        AL, caches = L_model_forward(X, parameters)
        cost       = compute_cost(AL, Y)
        grads      = L_model_backward(AL, Y, caches)
        parameters = update_parameters(parameters, grads, learning_rate)

        if print_cost and i%100==0:
            costs.append(cost)
            print("cost after iteration %i: %f" % (i,cost))

    plt.plot(np.squeeze(costs))
    plt.xlabel('iterations (per 100)')
    plt.ylabel('cost')
    plt.title("learning rate = " + str(learning_rate))
    plt.show()

    return parameters   


# 4、运行两层模型
'''
n_x = train_x.shape[0]
n_h = 7
n_y = 1
layers_dims = [n_x, n_h, n_y]

parameters = two_layer_model(train_x, train_y, layers_dims, 
                             learning_rate=0.01, num_iterations=2500, print_cost=True)

predictions_train = predict(train_x, train_y, parameters)
predictions_test  = predict(test_x, test_y, parameters)
'''

# 5、运行L层模型
layers_dims = [train_x.shape[0], 20, 7, 5,  1]
print(layers_dims)

parameters = L_layer_model(train_x, train_y, layers_dims,
                           learning_rate=0.01, num_iterations = 1000, print_cost = True)

predictions_train = predict(train_x, train_y, parameters)
predictions_test  = predict(test_x, test_y, parameters)


'''
# 6、显示一些标记不正确的图像
print_mislabeled_images(classes, test_x, test_y, predictions_test)

# 7、用自己的图像测试
my_image = "my_image.jpg" # change this to the name of your image file 
my_label_y = [1]          # the true class of your image (1 -> cat, 0 -> non-cat)

fname = "images/" + my_image
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(num_px,num_px)).reshape((num_px*num_px*3,1))
my_predicted_image = predict(my_image, my_label_y, parameters)

plt.imshow(image)
plt.show()
print ("y = " + str(np.squeeze(my_predicted_image)) +", your L-layer model predicts a \"" \
       + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")
'''