本节讲解求解线性方程组的一种写法克拉姆法则(Cramer)
1 克拉姆法则
解线性方程组 Ax = u (A是可逆矩阵) 的克拉姆法则如下:
2 克拉姆法则的证明
首先方程组的解可写为以下形式:
因为Aej等于A的第j列aj,因此有:
将A的第k列换成u后得到Ak:
计算Ak的行列式并由行列式的多重线性性质可得:
由行列式性质可知上式仅仅第k项非零:
因为A可逆 所以detA不等于0,于是:
根据拉普拉斯公式 将detAk按第k列展开得到:
带入上式得到计算方程组解的克拉姆法则:
克拉姆法则就是通过计算行列式求解方程组,但是当矩阵规模较大时 ,计算量大大超过消元法。
3 克拉姆法则求解线性方程组示例
假设如下线性方程组 并假设矩阵可逆:









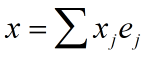
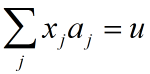
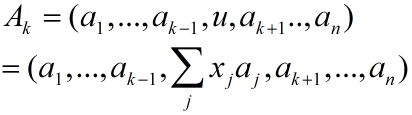
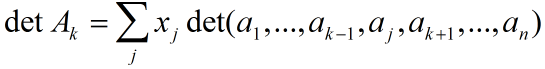
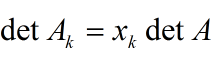
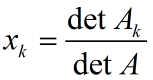
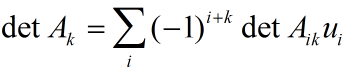

















 673
673

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








