Householder Flow

Householder Flow

变分自动编码器(VAE)是可扩展的、强大的生成模型。然而，变分后验的选择决定了VAE的可操作性和灵活性。一般来说，潜变量是用一个对角协方差矩阵的正态分布建模的。这可以提高计算效率，但通常不能灵活地匹配真实的后验分布。丰富变分后验分布的一种方法是应用正则化流，即normalizing flows。这种操作是对潜变量的简单后验分布做一系列可逆变换，将其变为复杂，灵活的后验分布。Householder Flow就是normalizing flows中的一种。

数学原理

1. 随机变量的函数的概率密度
已知$X\sim p_X(x),Y=f(X)，f(X)是可逆函数，求Y的概率密度函数p_Y(y)？$
连续型随机变量的概率分布函数的形式是
$$F_X(x)=p(X<x)={\int }_{-\infty }^{x}p(t)dt$$
假如$f(x)$为增函数：
$$\begin{gathered} F_Y(y)=p(Y<y)=p(f(X)<y)=p(X<f^{-1}(y)) \\ =F_X(f^{-1}(y)) \end{gathered}$$

$$\begin{gathered} p_Y(y)=\frac{d{F}_Y(y)}{dy}=\frac{d{F}_X(f^{-1}(y))}{dy}=p(f^{-1}(y))\frac{d{f}^{-1}(y)}{dy} \\ 也可以写成: \\ {p}_Y(y)=p(x)\frac{dx}{dy} \end{gathered}$$
假如$f(x)$为减函数：
$$\begin{gathered} F_Y(y)=p(Y<y)=p(f(X)<y)=p(X>f^{-1}(y)) \\ =1-F_X(f^{-1}(y)) \end{gathered}$$

$$\begin{gathered} p_Y(y)=\frac{d{F}_Y(y)}{dy}=\frac{d(1-F_X(f^{-1}(y)))}{dy}=-p(f^{-1}(y))\frac{d{f}^{-1}(y)}{dy} \\ 也可以写成: \\ {p}_Y(y)=-p(x)\frac{dx}{dy} \end{gathered}$$
所以综上：
$$p_Y(y)=p(f^{-1}(y))|\frac{d{f}^{-1}(y)}{dy}|或者p(x)|\frac{dx}{dy}|\text{\hspace{1em}(1)}$$

上面括号内部用到了求解不等式的方法，$f(X)<y$就相当于解不等式，当$f$是增函数时，不等式的解是$X<f^{-1}(y)$，当$f$是减函数时，不等式的解是$X>f^{-1}(y)$，不理解的同学可以用一元一次不等式手动理解一下。

2. Normalization flow

对（1）式变形
$$p(y)=p(x)|\frac{dx}{dy}|=p(x)|\frac{dx}{df(x)}|=p(x)|\frac{df(x)}{dx}{|}^{-1}$$
所以有下式成立：
$$\begin{gathered} x\sim p(x) \\ y=f(x) \\ y\sim p(y)=p(x)|\frac{df}{dx}{|}^{-1} \end{gathered}$$
如果x是一个高维向量，那么就变成下式：
$$y\sim p(y)=p(x)|det\frac{df}{dx}{|}^{-1}\text{\hspace{1em}(2)}$$

$|det\frac{df}{dx}|$是雅克比行列式的绝对值。

如果我们施加的一系列的$f_k,k\in [1,K]$，那么就得到一个归一化流（normalizing flows）：
$$\begin{gathered} z_K=f_K\ast ...\ast f_1(z_0)，z_0\backsim q_0(z_0) \\ {z}_K\backsim q_K(z_K)=q_0(z_0)\prod _{k=1}^K|det\frac{d{f}_k}{d{z}_{k-1}}{|}^{-1} \end{gathered}$$

这一系列变换就可以将一个简单的概率分布变成一个复杂的概率分布。

3. LOTUS
LOTUS全称是law of unconscious statistician，具体规则就是：
$$E_{q_K(z_K)}[h(z_K)]=E_{q_0(z_0)}[h(f_K\ast ...\ast f_1(z_0))]$$

也就是在关于$h(z_K)$求$q_K(z_K)$的期望时，可以转为求$q_0(z_0)$的期望。

ELBO

通过normalizing flows，我们可以将变分后验变为如下：
$$ln{q}_K(z_K)=ln{q}_0(z_0|x)-\sum _{k=1}^{K}ln|det\frac{d{f}_k}{d{z}_{k-1}}|\text{\hspace{1em}(3)}$$

VAE中的变分下界有两种形式：

或者：

第二种形式可以由第一种得到，我们看第一种形式，结合前面提到的LOTUS规则将变分下界(ELBO)变为：

Householder transformation

假设$v$是一个与超平面正交的向量（Householder vector），那么Householder matrix$H$定义如下：
$$H=I-2\frac{v{v}^T}{|v{|}^2}$$
$H$矩阵也是一个正交矩阵，所以其雅可比行列式的绝对值为1，也就是$ln|detH|=0$。
我们令$f_k=H_k{z}_{k-1}$，那么（4）式中

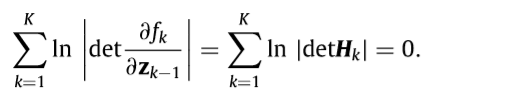
所以（4）式中只需要计算两项。

因此，后验分布$z_0$通过一系列的Householder transformation（被称作Householder Flows）转化为了$z_K$，这样$z_K$就可以看做是由一个复杂的分布中采样出来的，可以更加灵活的建模真实的后验分布。