寻找凸包 convex hull(二)——Graham_Scan

这篇继续凸包得的寻找，上篇文章中使用了暴力的方法，在网上又看了一些资料下面会介绍常用的算法 Graham_Scan

首先介绍一下有向面积的概念：

算法的大致步骤：

1）对于给定的点集 data 寻找其中y坐标最小的点作为起始点p

2)  把坐标原点移动到p处，然后计算每个点与x轴正方向的夹角

3）根据夹角的大小排序，得到排序后的点集data

4）设点集data中有N个数据，数组CHS用来保存满足条件的边界点

      把data[N-1]和data[0]放入CHS中，然后放入data[1],如果CHS[0](data[N-1]),CHS[1](data[0]),CHS[2](data[1])，

三点构成的三角形有向面积为正（注意CHS[0]是起点,CHS[2]是终点），则认为data[1]满足边界条件继续把data[2]放入CHS中；

放入data[2]后如果发现CHS[1](data[0]),CHS[2](data[1]),CHS[3](data[2])，构成的有向面积为负，那么判断data[1]是不满足条件的，

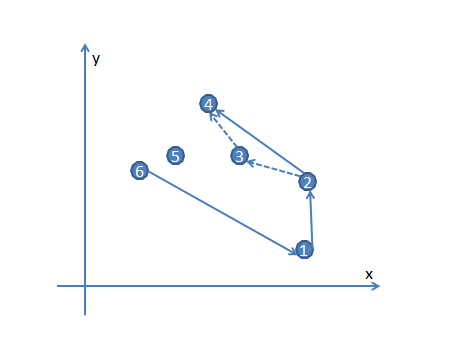
需要删除；接着按照上面的规律放入剩余的全部数据；示意图如下

上图中序号越大，夹角越大。先把6号和1号放入数组CHS中，扫描2号发现612满足逆时针条件；当按照夹角由小到大扫描时会先扫描到3号，而123组合满足逆时针条件；接着扫描到4号，234组合不满足逆时针条件，所以就要删除3号直接连接24号，此时124组合满足逆时针条件；接着就是扫描5号，观察245是否满足逆时针条件

下面贴上代码

#include "stdafx.h"
#include "convexhull.h"
#include <cmath>
#include <cstdlib>

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

#define Width 640
#define Height 480
#define PointNum 18
struct _Point
{
	Point pt;
	float angle;
	void operator=(const _Point &pp)
	{
		this->pt = pp.pt;
		this->angle = pp.angle;
	}
	bool operator >(const _Point &pp)
	{
		return(this->angle > pp.angle);
	}
};

static vector<_Point> data(PointNum);//原始数据

static vector<_Point> CHS(PointNum);//保存最后结果

static int sp = 0;	//用来指示数组CHS的下标
//计算有向面积
//如果 返回值大于零则ABC是按照逆时针分布,=0 ABC在一条直线上,<0 ABC顺时针分布
int cross(Point A, Point B, Point C)
{
	return(A.x*B.y + B.x*C.y + C.x*A.y - A.y*B.x - B.y*C.x - C.y*A.x);
}
//
void Swap(_Point &a, _Point &b)
{
	_Point temp = a;
	a = b;
	b = temp;
}
//随机产生点
void generatePoint(vector<_Point> & input)
{
	RNG rng(1234);
	for (int i=0; i<PointNum; i++)
	{
		input[i].pt.x = rng.uniform(50, 540);
		input[i].pt.y = rng.uniform(50, 400);
	}
}

//简单排序
template<class T>
void bubbleSort(T & a, int n)
{
	//for (int i=0; i<n-1 ; i++)
	//{
	//	for (int j=i+1; j<n; j++)
	//	{
	//		if(a[i]>a[j])
	//		{
	//			Swap(a[i], a[j]);
	//		}
	//	}
	//}
	bool changed = true;
	for (int i=0; i<n && changed; i++)
	{
		for (int j=0; j<n-i-1; j++)
		{
			changed = false;
			if(a[j] > a[j+1])
			{
				Swap(a[j], a[j+1]);
				changed = true;
			}
		}
	}
}
//Graham Scan 算法的实现
void GrahamScan()
{
	for(int i=0; i<data.size(); i++)//寻找y值最小的点
	{
		if(data[0].pt.y > data[i].pt.y)
			Swap(data[0], data[i]);
	}
	//移动坐标系原点到data[0]处
	for(int i=0; i<data.size(); i++)
	{
		data[i].pt.x -= data[0].pt.x;
		data[i].pt.y -= data[0].pt.y;
		data[i].angle = atan2((float)data[i].pt.y, (float)data[i].pt.x);
	}
	//按与x轴夹角由小到大排序
	bubbleSort(data, data.size());
	for(int i=0; i<data.size(); i++)
		cout<<data[i].angle<<endl;

	CHS[0] = data[PointNum-1];
	CHS[1] = data[0];

	int k = 1;
	sp = 2;
	while(k < data.size())
	{
		CHS[sp] = data[k];
		if(cross(CHS[sp-2].pt, CHS[sp-1].pt, CHS[sp].pt) > 0)//如果连续的三点为逆时针则选中当前点
		{		
			k++;
			sp++;
		}
		else	//如果为顺时针则要剔除上一个点
		{
			sp--;
		}
	}
}


void GradamScan_test()
{
	Mat img;
	img.create(Size(Width, Height), CV_8UC3);

	generatePoint(data);

	GrahamScan();

	for (int i=0; i<data.size(); i++)
	{
		circle(img, data[i].pt, 10, Scalar(0,0,255));
	}

	for (int i=0; i<sp-1; i++)
	{
		line(img, CHS[i].pt, CHS[i+1].pt, Scalar(0,0,255), 2, 8);
		imshow("ss", img);
		waitKey(1000);
	}
}

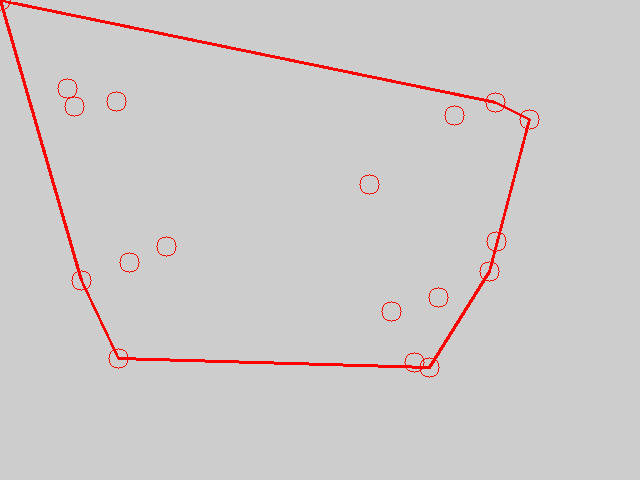
运行函数GradamScan_test，结果如下图