决策树分类
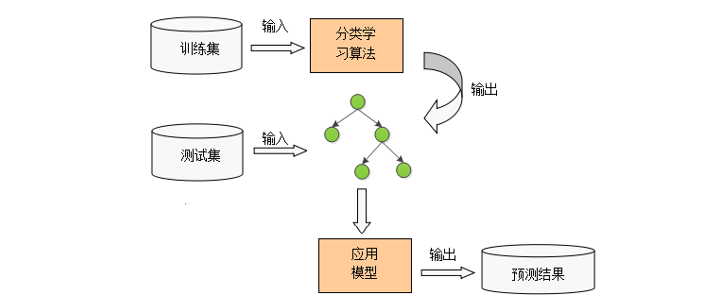
决策树模型呈树形结构,在分类中,表示基于特征对实例进行分类的过程。可以认为是if-then规则的集合。
决策树组成部分
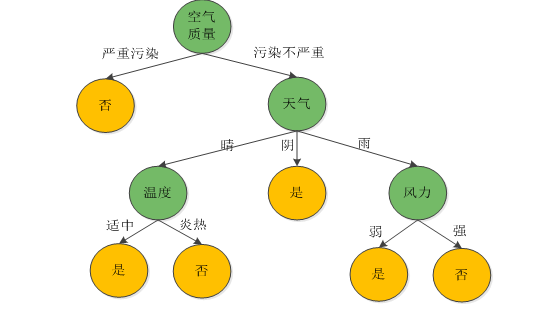
决策树是一种描述对样本实例(天气情况)进行分类(进行户外活动,取消户外活动)的树形结构。
决策树由结点(node)和有向边(directed edge)组成。结点分为内部结点和叶结点。内部结点表示一个特征属性(空气质量/天气/温度/风力),有向边表示对应的特征属性下的分支;叶结点表示决策结果(进行活动/取消活动)。
最上面的结点是根结点,此时所有样本都在一起,经过该结点后样本被划分到各子结点中。每个子结点再用新的特征来进一步决策,直到最后的叶结点,就不需要再进行划分。
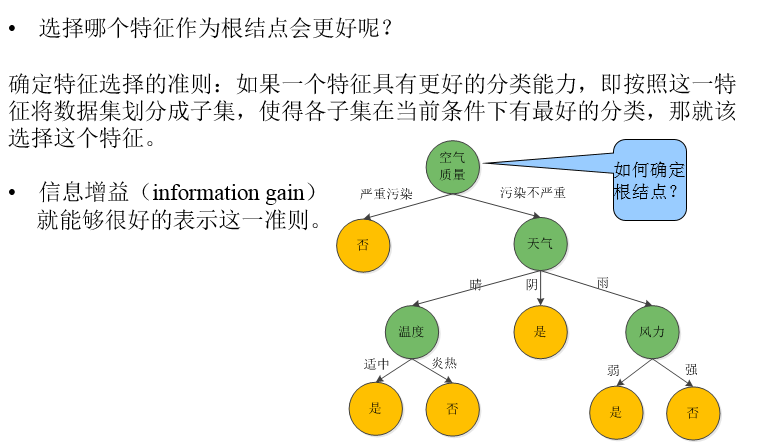
特征选择
决策树—ID3算法
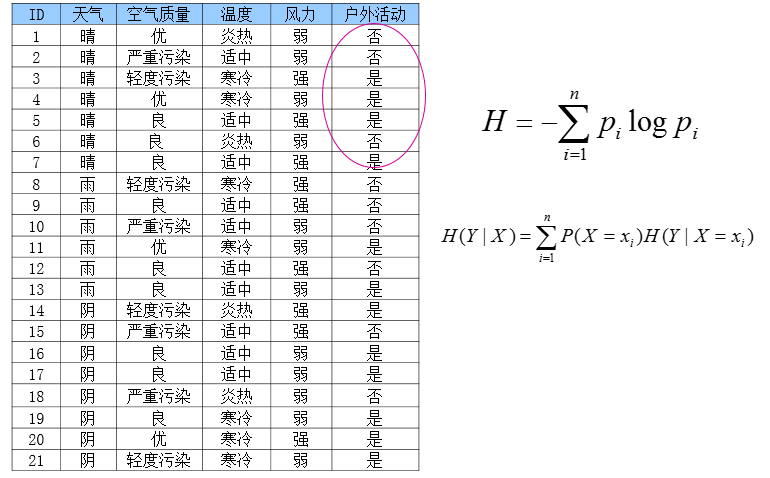
熵(entropy)
条件熵
决策树应用类型
信息增益

ID3思想
ID3算法实例
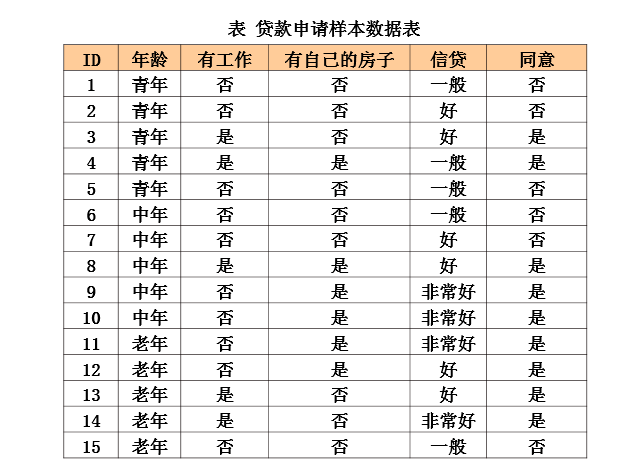
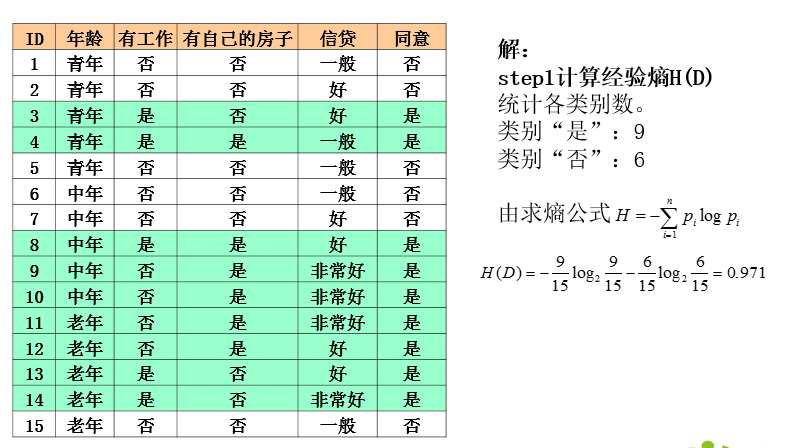
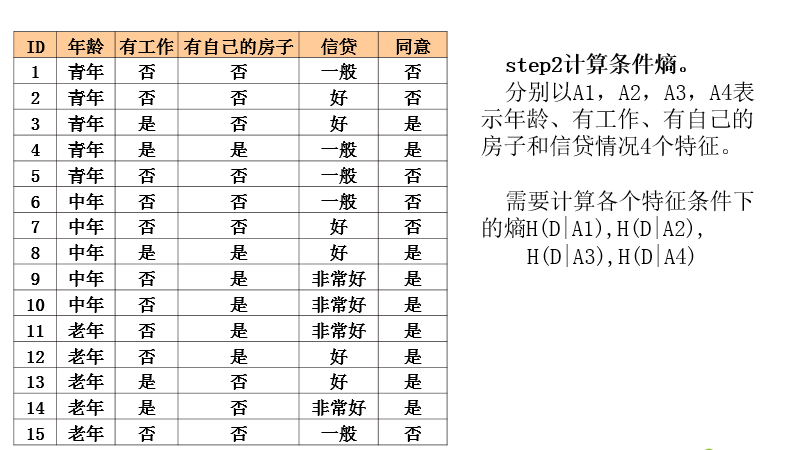
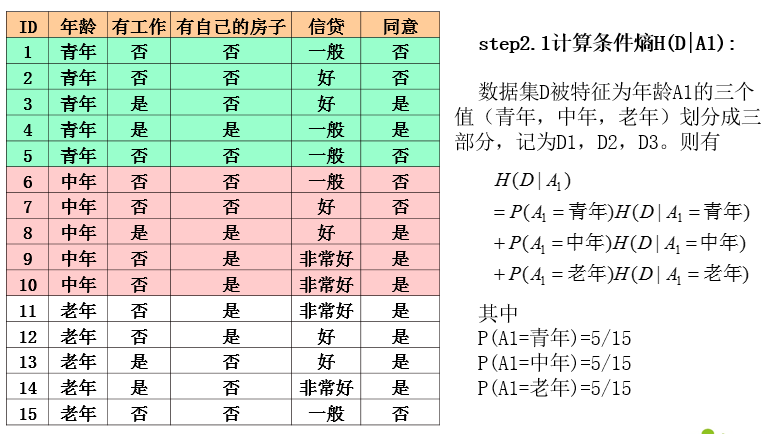
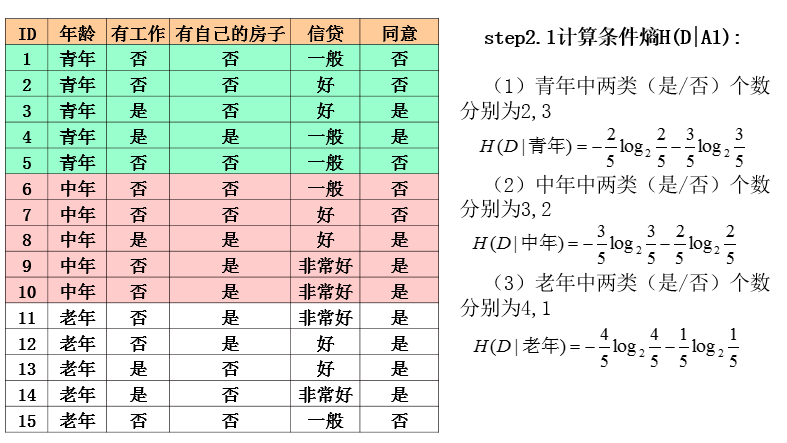
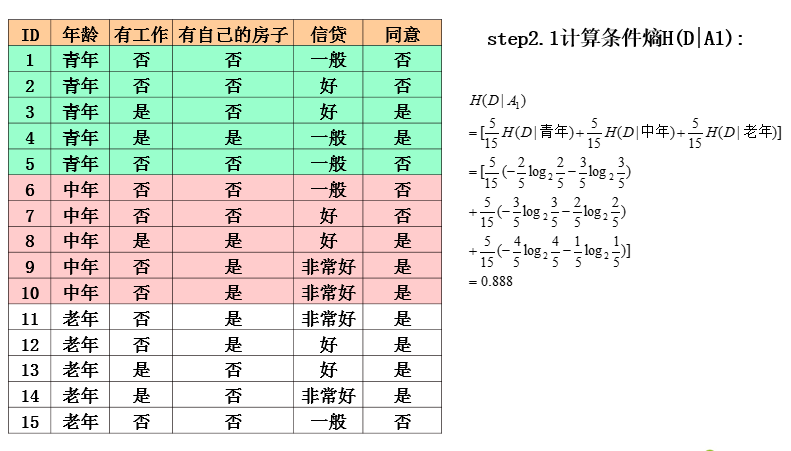
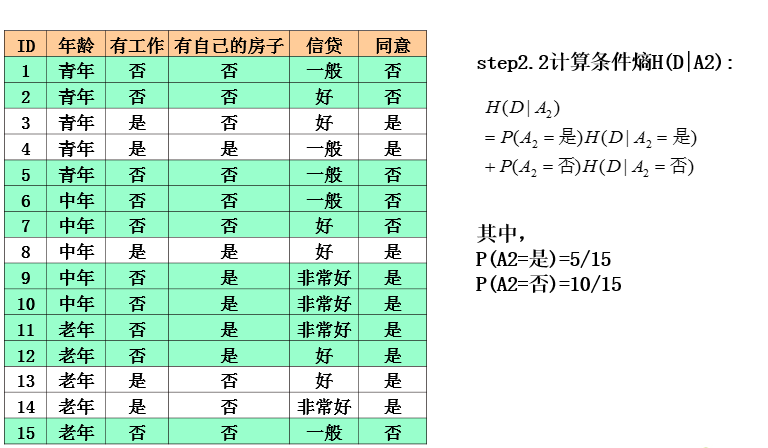
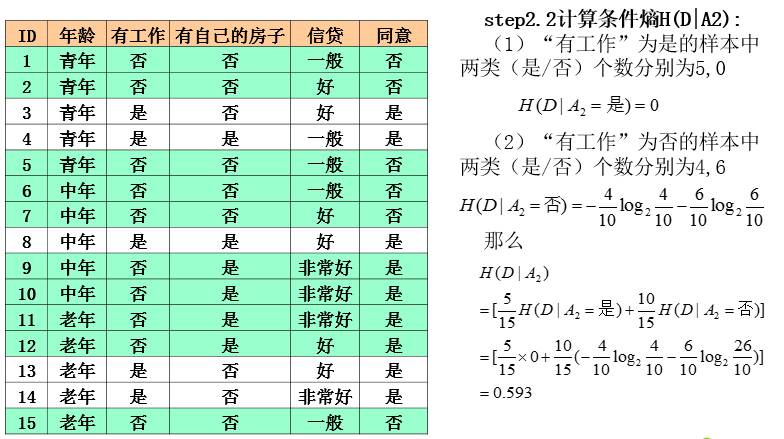
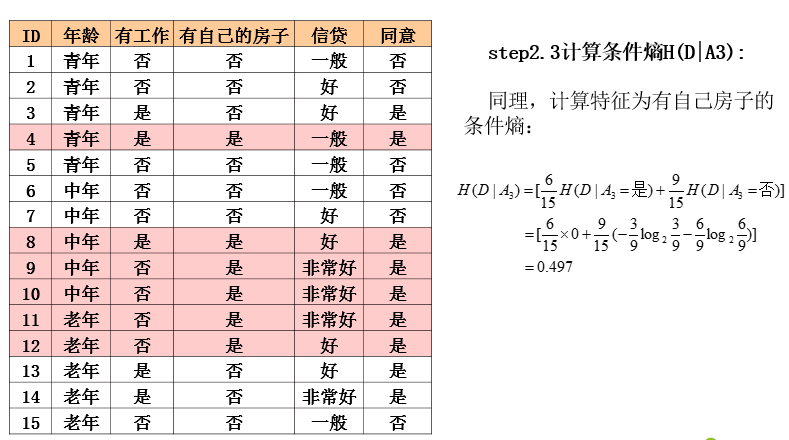
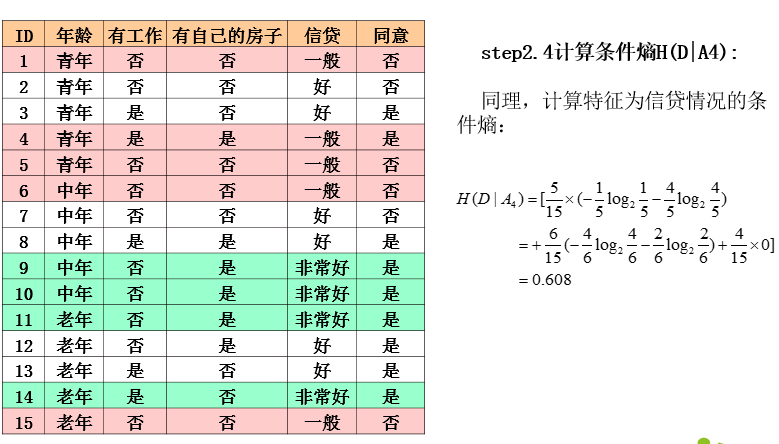

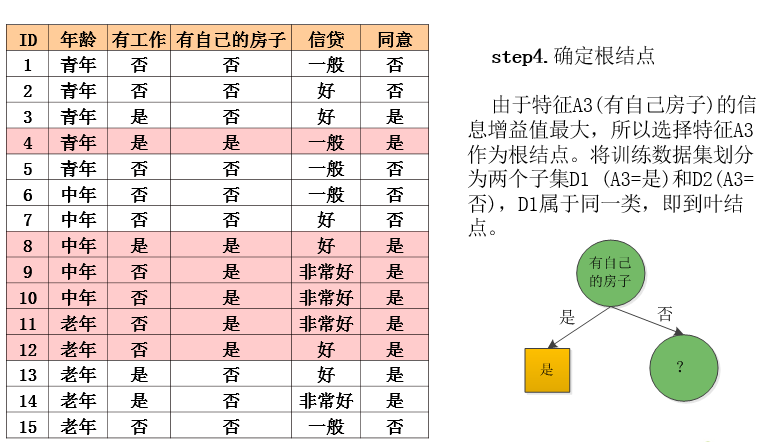
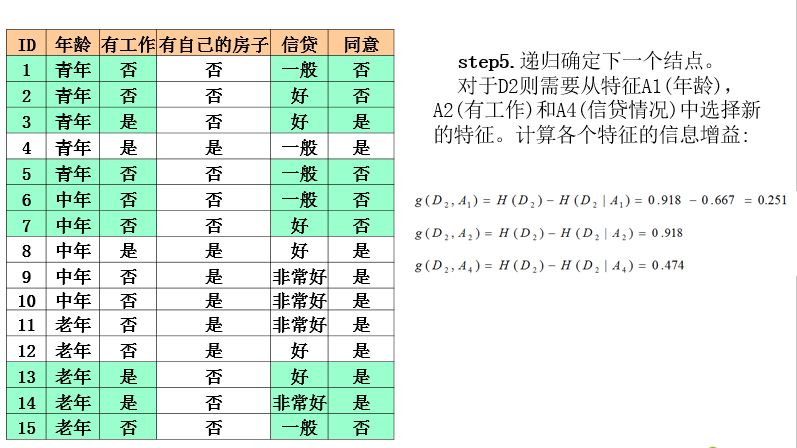
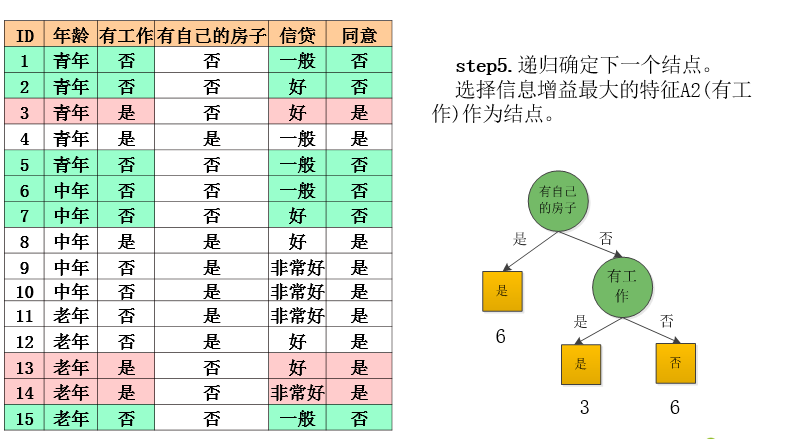
ID3算法分析
C4.5算法的改进
信息增益比
CART算法

基尼指数
CART生成树
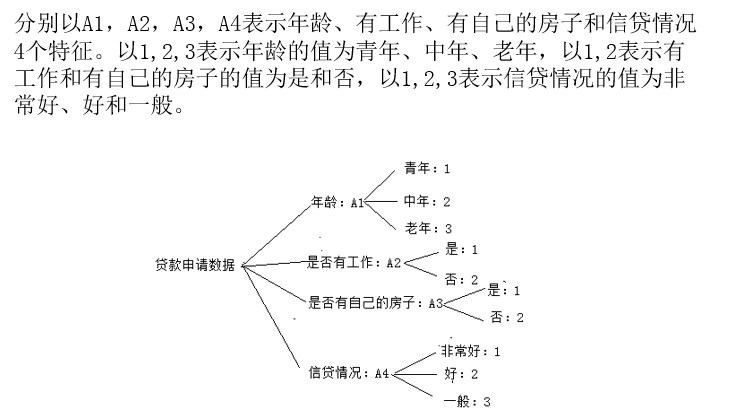
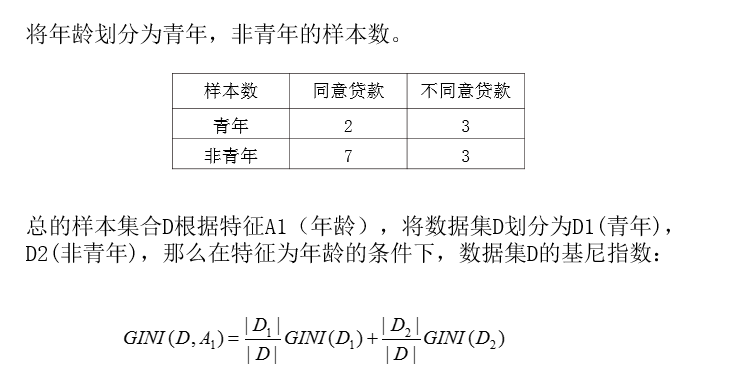

CART剪枝
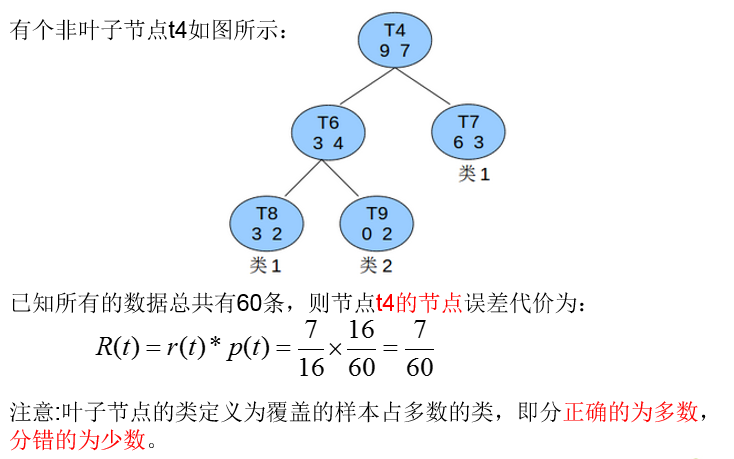
剪枝—代价复杂度CCP
















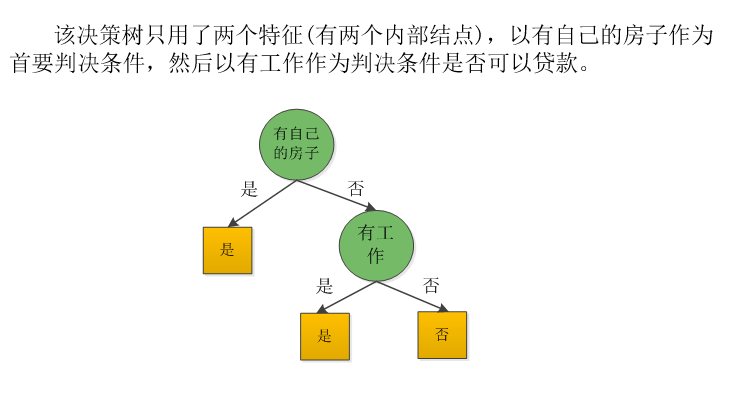



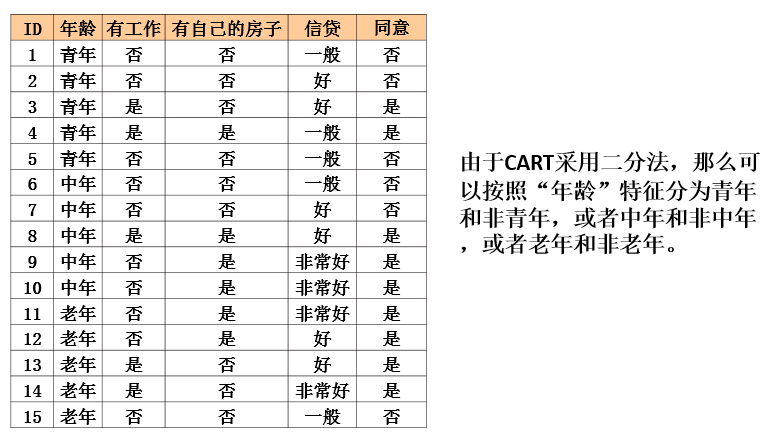



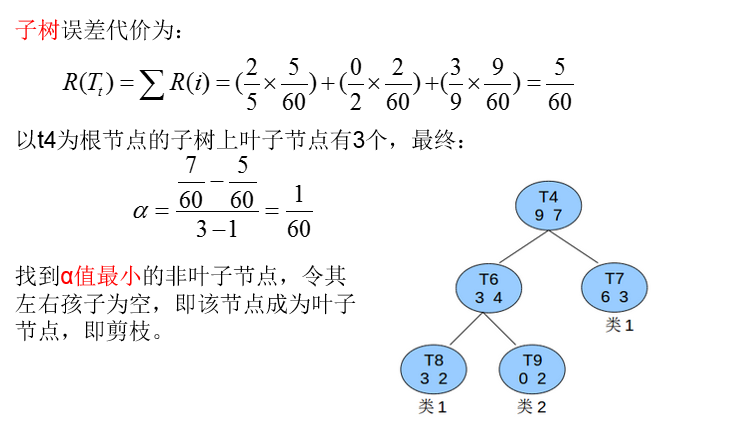
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








