K-means聚类算法

原创已于 2025-05-02 18:53:20 修改 · 1k 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #kmeans #聚类

于 2025-04-30 23:15:20 首次发布

1.聚类

聚类分析（clustering）属于机器学习领域中无监督学习（unsupervised learning）的范畴，其能够在没有先验知识或标签信息的情况下，通过挖掘数据中的内在结构和规律，将数据对象自动划分为若干个“类”或“簇”，使得在同一个簇中的对象具有较高的相似度，而不同簇的对象之间差别较大。聚类算法在模式识别、医学诊断、生物学等领域中有广泛的应用。例如，在市场分析中，企业可以通过聚类算法将客户划分为不同的群体，从而精准地制定营销策略；在生物医学领域，聚类可用于基因表达数据的分析，揭示基因之间的相互作用关系。

2.K均值（K-means）聚类算法

K-means算法是一种简单高效的迭代算法，该算法可以将数据集划分为k个预定义的不同非重叠子组，其中每个数据点只属于一个组。其核心思想是将数据集中的n个数据点划分为k个聚类，使得每个对象到其所属聚类的中心的距离之和最小。

3.常见的距离度量方法

欧几里得距离（Euclidean Distance）：是一个通常采用的距离定义。在二维和三维空间中的欧氏距离的就是两点之间的距离。在二维空间中，两点间的欧几里得距离计算如下图所示：

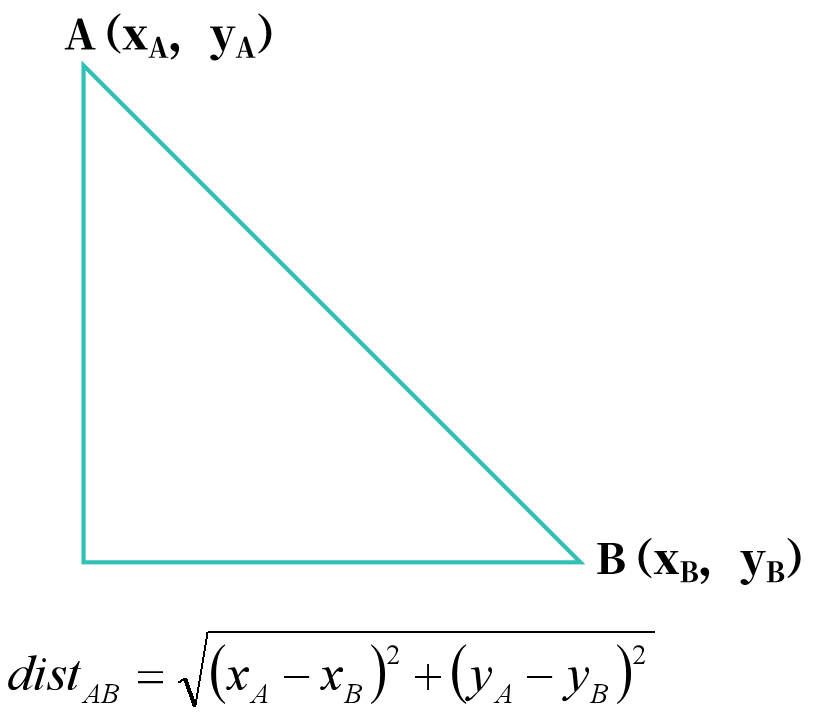
在n维空间中，两点间的欧几里得距离公式为：

$dist_{xy}=\sqrt{\left( x_1-y_1 \right) ^2+\left( x_2-y_2 \right) ^2+\cdots +\left( x_n-y_n \right) ^2}\\=\sum_{i=1}^n{\left( x_i-y_i \right)}^2$

曼哈顿距离(Manhattan Distance)：曼哈顿距离也称出租车几何，用以标明两个点在标准坐标系上的绝对轴距总和。在二维空间中，两点间的曼哈顿距离计算如下图所示：

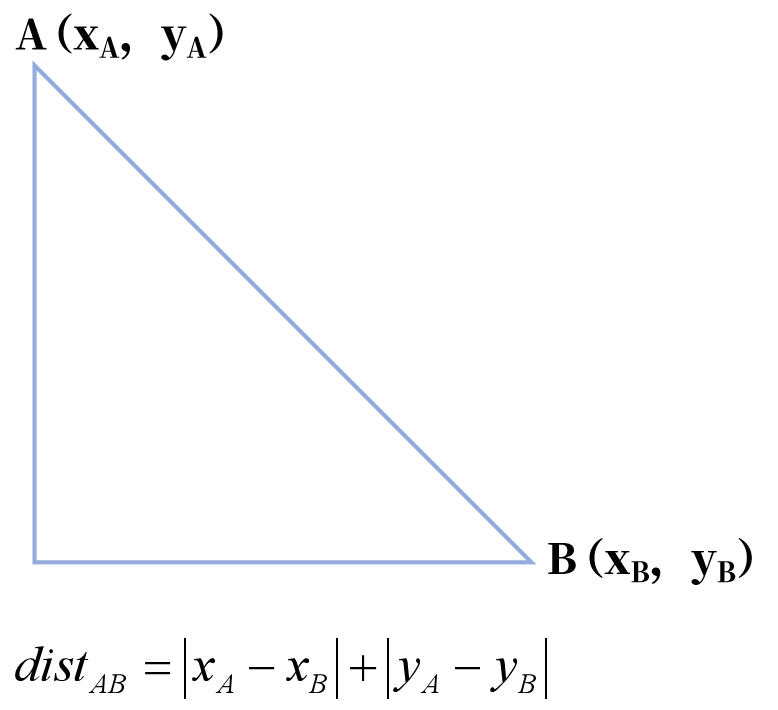
在n维空间中，两点间的曼哈顿距离公式为：

$dist_{xy}=\left|x_1-y_1\right|+\left|x_2-y_2\right|+\cdots+\left|x_n-y_n\right|=\sum_{i=1}^n\left|x_i-y_i\right|$

切比雪夫距离(Chebyshev Distance)：切比雪夫距离是向量空间中的一种度量，两个点之间的切比雪夫距离定义为其各坐标数值差的绝对值中的最大值。在二维空间中，两点间的切比雪夫距离计算如下图所示：

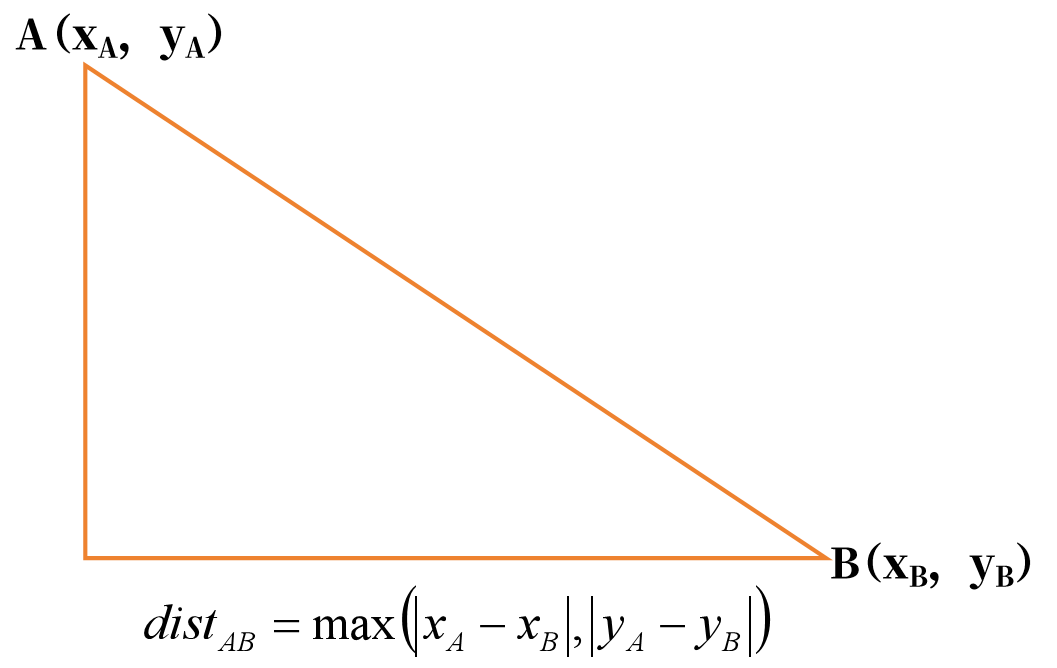
在n维空间中，两点间的切比雪夫距离公式为：

$dist_{xy}=\max(\left|x_1-y_1\right|,\left|x_2-y_2\right|,\cdots,\left|x_n-y_n\right|)$

4.K-means算法步骤

①设定参数k：k表示需要将数据聚为几类；

②初始化聚类中心：随机选择k个中心点；

③以距离为衡量标准进行聚类：计算每一样本到各中心的距离，将每个样本指派到与其最近的中心对应的类中；

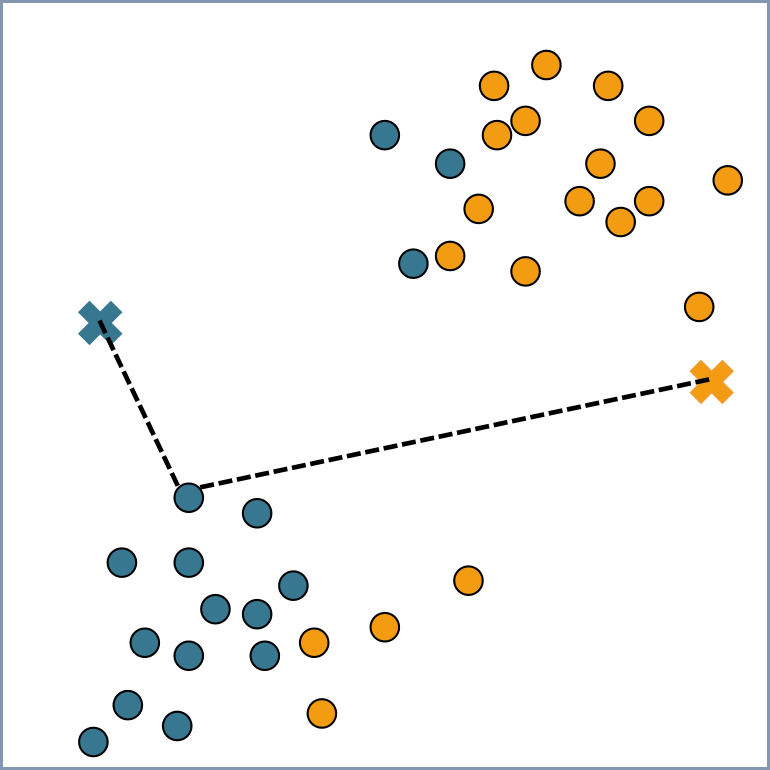
④更新聚类中心：求聚类后各类别新的聚类中心；

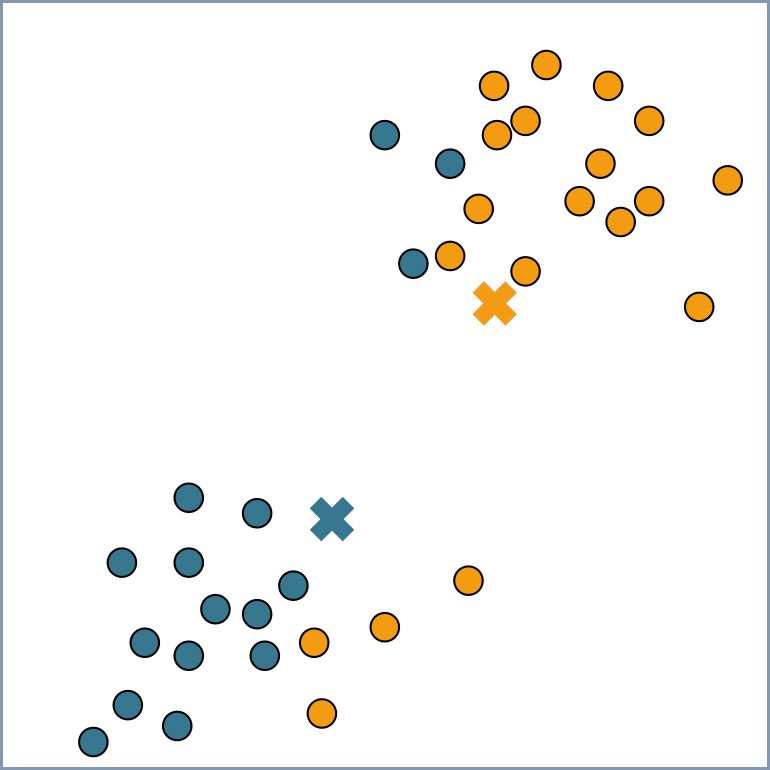
⑤重复步骤③、④，直至聚类中心不再改变，可视为聚类完成；

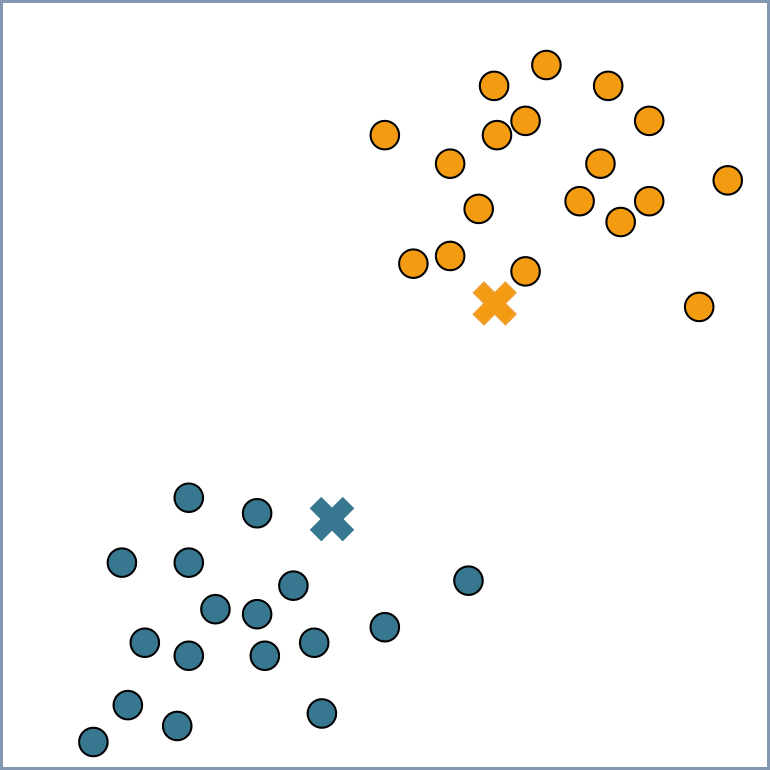
5.代码实现

def get_Euclidean_dist(vector1,vector2):
    # 两点间的距离采欧几里得距离
    dim=vector1.size
    temp=0
    for i in range(dim):
        temp+=(vector1[i]-vector2[i])**2
    dist=np.sqrt(temp)
    return dist

def init_centroids(samples,k):
    # 在样本点中随机采样k个点作为初始化聚类中心
    samples_num=samples.shape[0]
    samples_dim=samples.shape[1]
    rand_idx=random.sample(range(samples_num),k)
    centroids_init=np.zeros(shape=(k,samples_dim))
    for i in range(k):
        idx=rand_idx[i]
        centroids_init[i]=samples[idx].copy()
    return centroids_init

def get_closest_centroid_idx(sample,centroids):
    # 计算距离样本点最近的聚类中心
    centroids_num=centroids.shape[0]
    closest_idx=0
    min_dist=get_Euclidean_dist(sample,centroids[0])
    for i in range(1,centroids_num):
        dist=get_Euclidean_dist(sample,centroids[i])
        if dist<min_dist:
            closest_idx=i
            min_dist=dist
    return closest_idx

def create_clusters(samples,centroids,k):
    # 创建簇
    clusters=[[] for i in range(k)]
    samples_num=samples.shape[0]
    for i in range(samples_num):
        closest_idx=get_closest_centroid_idx(samples[i],centroids)
        clusters[closest_idx].append(samples[i])
    return clusters

def update_centroids(clusters,centroids):
    # 更新聚类中心
    clusters_num=len(clusters)
    centroids_update=np.zeros_like(centroids)
    for i in range(clusters_num):
        cluster=np.array(clusters[i])
        # 聚类中心即各个簇中所有样本点各坐标分量的均值
        centroid=cluster.mean(axis=0)
        centroids_update[i]=centroid
    return centroids_update

def plot_clusters(clusters,sample_dim,centroids):
    # 绘图
    clusters_num=len(clusters)
    fig=plt.figure()
    if sample_dim==2:
        ax=fig.add_subplot()
    else:
        ax=fig.add_subplot(projection='3d')
    if sample_dim==2:
        for i in range(clusters_num):
            cluster=np.array(clusters[i])
            ax.scatter(cluster[:,0],cluster[:,1],edgecolors='k',marker='o',s=40,alpha=0.6)
        ax.scatter(centroids[:,0],centroids[:,1],edgecolors='r',marker='x',c='r',s=60)
    else:
        for i in range(clusters_num):
            cluster=np.array(clusters[i])
            ax.scatter(cluster[:,0],cluster[:,1],cluster[:,2],edgecolors='k',marker='o',s=40,alpha=0.6)
        ax.scatter(centroids[:,0],centroids[:,1],centroids[:,2],edgecolors='r',marker='x',c='r',s=60)
    plt.show()

def K_means_Algorithm(samples,k,max_iter):
    # K-means算法
    centroids=init_centroids(samples,k)
    sample_dim=samples.shape[1]
    for i in range(max_iter):
        clusters=create_clusters(samples,centroids,k)
        pre_centroids=centroids.copy()
        centroids=update_centroids(clusters,pre_centroids)
        diff=centroids-pre_centroids
        if sample_dim==2 or sample_dim==3:
        	# 当样本空间为二维或三维空间时绘图
            plot_clusters(clusters,sample_dim,centroids)
        if not diff.any():
            # 当更新后的聚类中心与前次聚类中心无任何差异时, 跳出循环
            break

6.算法测试

为测试算法的有效性，需要先获取测试数据集。sklearn包提供了一系列数据集生成函数，能够便捷、灵活地生成本算法所需的数据集。

6.1 簇类数据集

sklearn.datasets.make_blobs(n_samples,n_features,centers,cluster_std,center_box, shuffle,random_state,return_centers)

n_samples：样本数，可为整数或数组，默认值为100。若为整数，则表示生成数据集的总样本数；若为数组，则表示每个簇的样本数；
n_features：每个样本的特征数（维数），默认值为2；
centers：簇中心，可为整数或数组，默认为无。若为整数，则表示生成的簇（类）的数量，此时随机指定各个簇的中心位置；若为数组，则该数组形状必须为(n_centers, n_features)，即自定义簇中心的位置；
cluster_std：标准差，可为浮点数或浮点数数组，用于控制簇的分散程度，标准差越大，簇中的样本越分散。若为浮点数，则各个簇的标准差均为此数；若为数组，则可分别指定各个簇的标准差；
center_box：簇中心边界框，为浮点数元组(最小值,最大值)，默认值为(-10.0,10.0)，用于当中心随机生成时，指定每个聚类中心的边界框；
shuffle：是否随机排列样本，布尔值，默认为True；
random_state：随机种子；
return_centers：是否返回簇中心，布尔值，默认为False。

该函数返回一个形状为(n_samples,n_features)的样本数组和一个长度为n_samples的标签数组。样本数组中每一行代表一个样本点，标签数组中每个数代表对应样本的真实标签。

if __name__=="__main__":
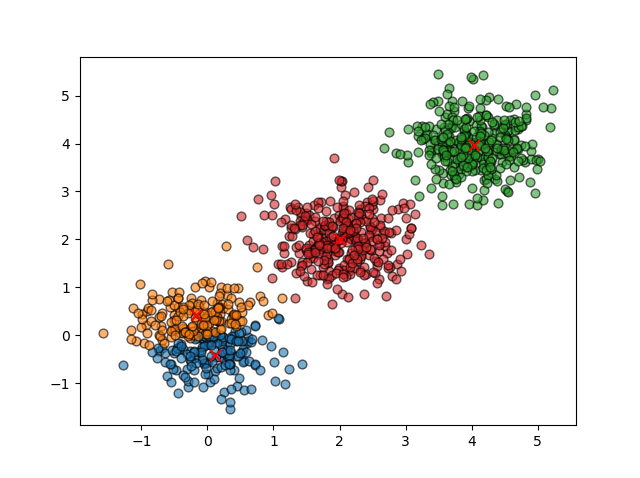
    # 生成500个二维样本点，指定三个簇中心为(0,0)、(2,2)、(4,4)，三个簇的样本差均为0.6
    samples0,true_label0=datasets.make_blobs(n_samples=500,
                                             n_features=2,
                                             centers=[[0,0],[2,2],[4,4]],
                                             cluster_std=0.6)
    K_means_Algorithm(samples0,3,100)

测试结果如下：

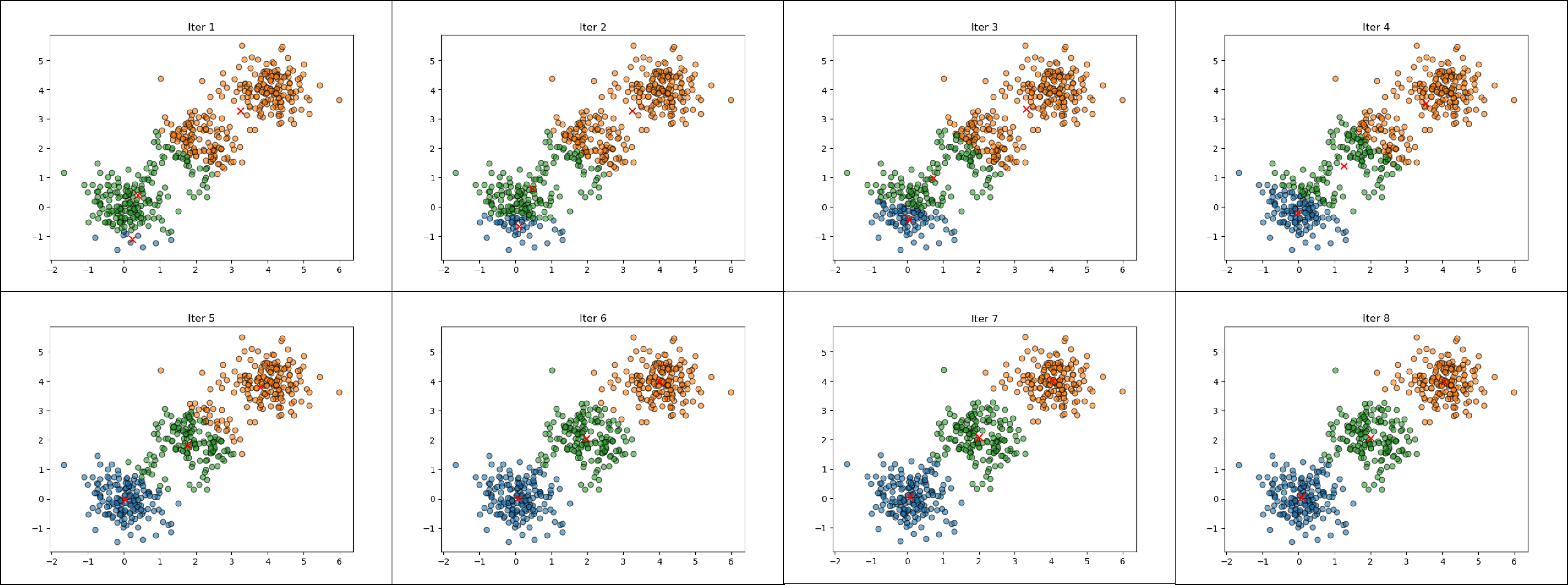
经过多次测试可以得出结论，在二维空间中，对于簇状分布的数据集，当k值设置得当时，K-means能够得到较好的聚类效果（聚类结果与直观相符）。

if __name__=="__main__":
	# 生成500个三维样本点，指定三个簇中心为(-2,-2,-2)、(0,0,0)、(2,2,2)，三个簇的样本差均为0.6
	samples1,true_label1=datasets.make_blobs(n_samples=500,
                                             n_features=3,
                                             centers=[[-2,-2,-2],[0,0,0],[2,2,2]],
                                             cluster_std=0.6)
	K_means_Algorithm(samples1,3,100)

测试结果如下：

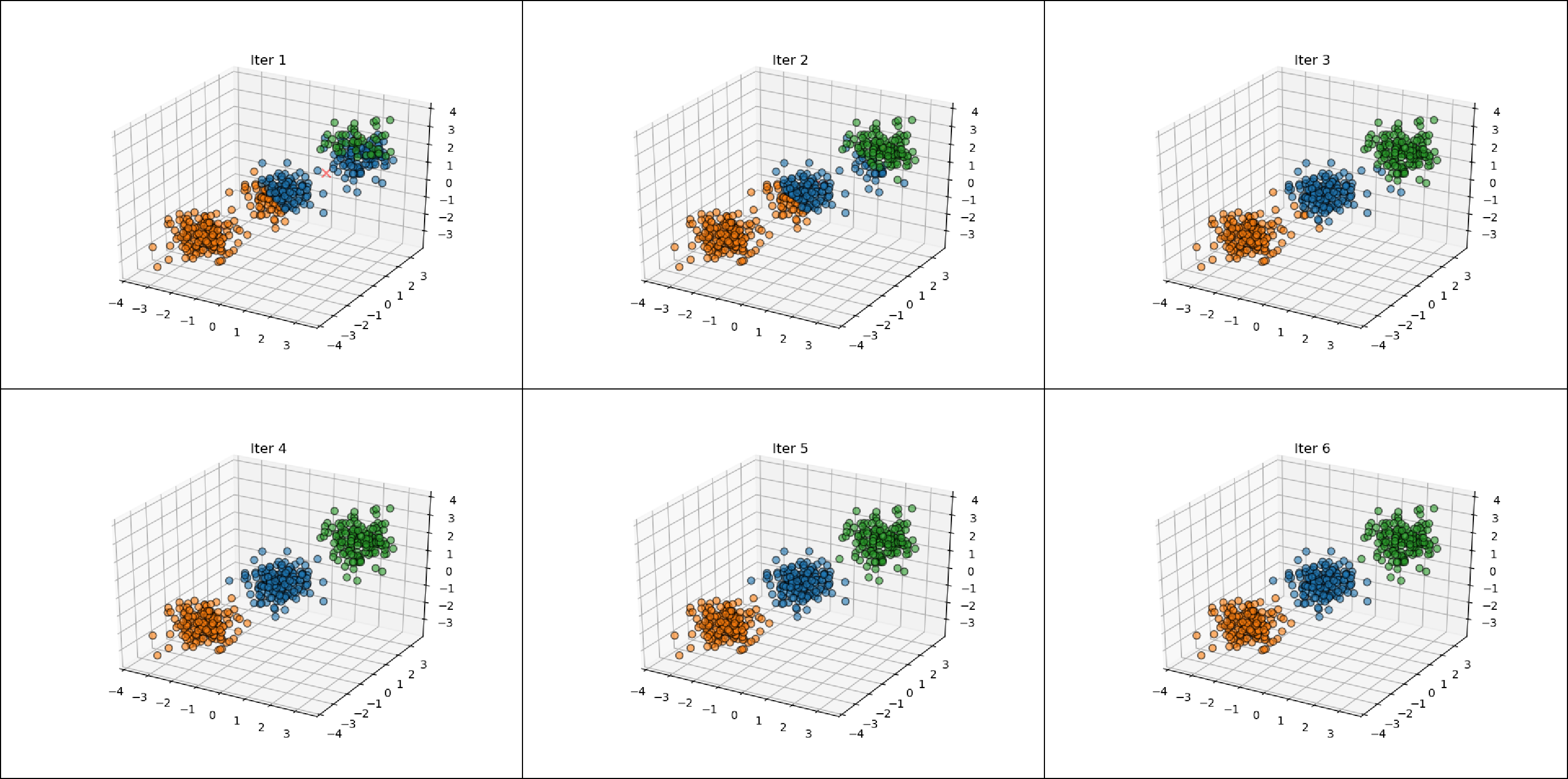
经过多次测试可以得出结论，在三维空间中，对于球状簇分布的数据集，当k值设置得当时，K-means能够得到较好的聚类效果（聚类结果与直观相符）。

6.2 环形数据集

sklearn.datasets.make_circles()用于生成两个环形的数据集。

sklearn.datasets.make_circles(n_samples,shuffle,noise,random_state,factor)

noise：高斯噪声，控制数据的分散程度；
factor：内外环形比例因子，取值[0,1)。

if __name__=="__main__":
	samples2,true_label2=datasets.make_circles(n_samples=500,
                                               noise=0.1,
                                               factor=0.5)
	K_means_Algorithm(samples2,2,100)

测试结果如下：

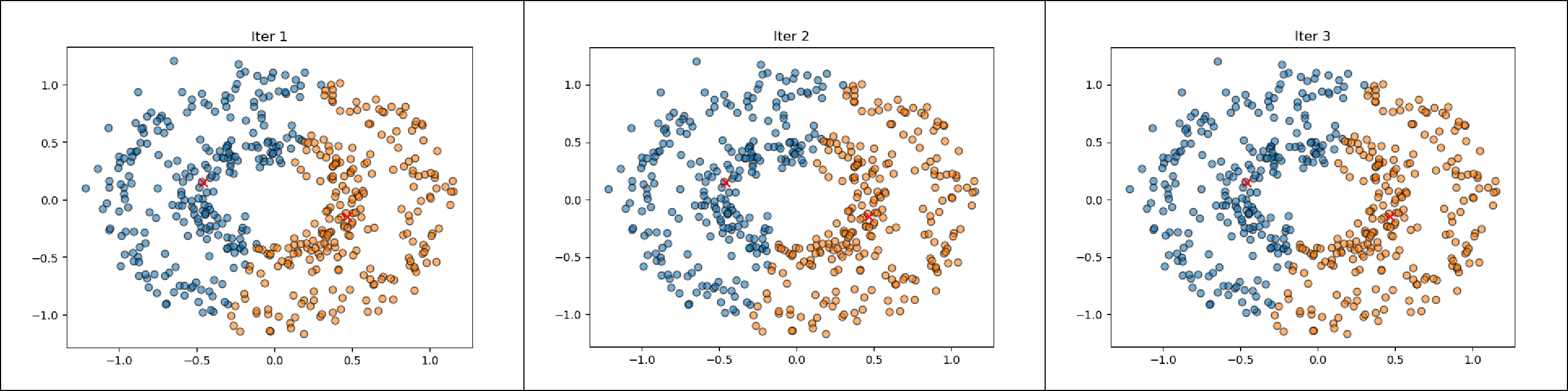
不难发现，该聚类结果与直观不相符（直观上的聚类结果应将内环聚为一类，外环聚为一类），且经过多次测试，均无法得到理想结果。

6.3 月牙形数据集

sklearn.datasets.make_moons()用于生成两个交错的月牙形数据集。

sklearn.datasets.make_moons(n_samples,shuffle,noise,random_state)

if __name__=="__main__":
    samples3,true_label3=datasets.make_moons(n_samples=500,noise=0.1)
    K_means_Algorithm(samples3,2,100)

测试结果如下：

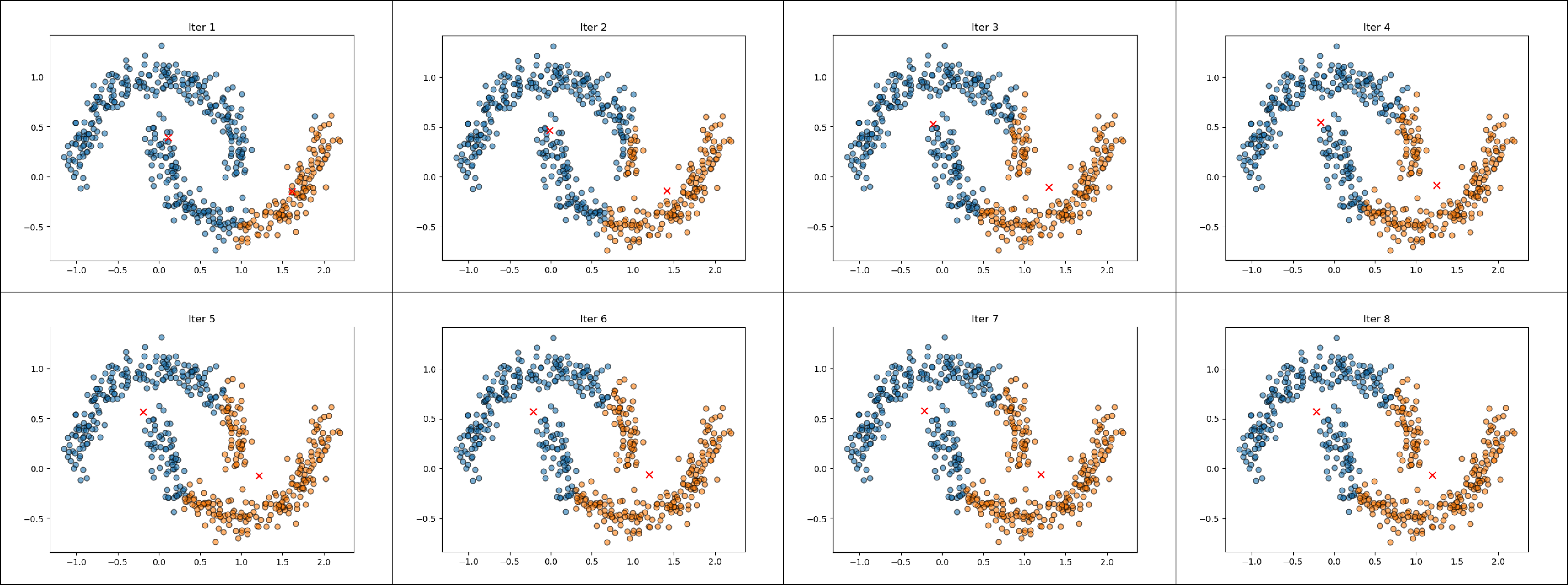
不难发现，该聚类结果与直观不相符（直观上的聚类结果应将两个月牙各聚为一类），且经过多次测试，均无法得到理想结果。

7. 总结

K-means算法是最常用的聚类算法之一，其主要优点如下：

①原理简单，易于实现，收敛速度快；

②可解释性强。

与此同时，该算法也存在如下缺点：

①需要人为设定k值，而k值的设定有赖于设置者对于数据的理解，若设定的k值不合理，则可能导致聚类结果不理想；

②对初始化聚类中心敏感，通常随机选取k个点作为初始化聚类中心，而不同的初始化聚类中心会对收敛速度产生影响；

③一般只能发现球状簇，对于环形、月牙形等分布的数据集（算法测试6.2、6.3），难以获得理想的聚类结果，这个问题可以通过改进的K-means算法解决。

7.1 k值的选择

K-means算法必须人为指定k值，而k值的指定大多依靠经验值。若指定的k值与数据集中的实际簇的数量不一致，则会导致聚类结果不佳。

如下图，实际簇的数量为4，但指定k=3，导致聚类结果不理想。

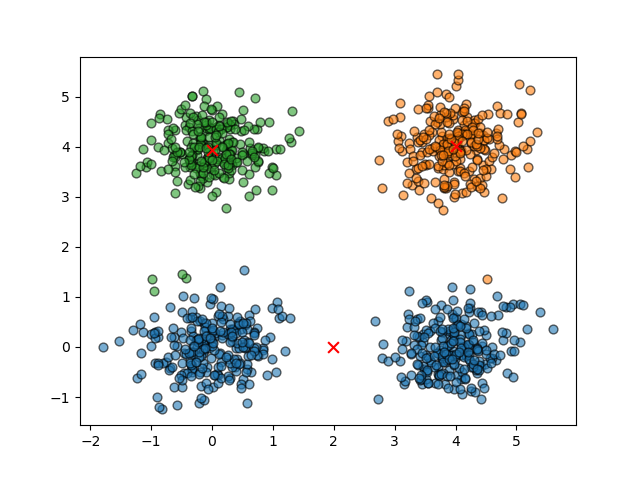
如下图，实际簇的数量为3，但指定k=4，导致聚类结果不理想。

在实际聚类应用中，数据集中的样本可聚为几类是难以判断的，为此，常采用手肘法（elbow method）来决定k的值。手肘法的核心思想是：随着聚类数量k的增加，每个聚类的误差平方和（Sum of Squared Errors, SSE, 即组内平方和）会逐渐减小。但是，当k增加到某个点之后，SSE 的下降速度会明显变缓。这个“SSE急剧下降转为缓慢下降”的转折点就像手肘的形状，因此称为“手肘法”，常将此转折点作为K-means算法k值的理想选择。

def elbow_method(samples,max_k):
    # 手肘法
    k_list=np.arange(2,max_k+1)
    SSE_list=[]
    for k in k_list:
        centroids=init_centroids(samples,k)
        while True:
            clusters=create_clusters(samples,centroids,k)
            pre_centroids=centroids.copy()
            centroids=update_centroids(clusters,pre_centroids)
            diff=centroids-pre_centroids
            if not diff.any():
                SSE=0
                for i in range(len(clusters)):
                    for sample in clusters[i]:
                        tmp=sample-centroids[i]
                        SSE=SSE+np.dot(tmp,tmp)
                SSE_list.append(SSE)
                break
    SSE_list=np.asarray(SSE_list)
    fig=plt.figure()
    plt.plot(k_list,SSE_list,marker='x',color='blue',alpha=0.8)
    plt.title('SSE-k Curve')
    plt.xlabel('k')
    plt.ylabel('SSE')
    plt.grid(ls='--',alpha=0.8)
    plt.show()

测试结果如下（此时测试数据的聚类数为3）：

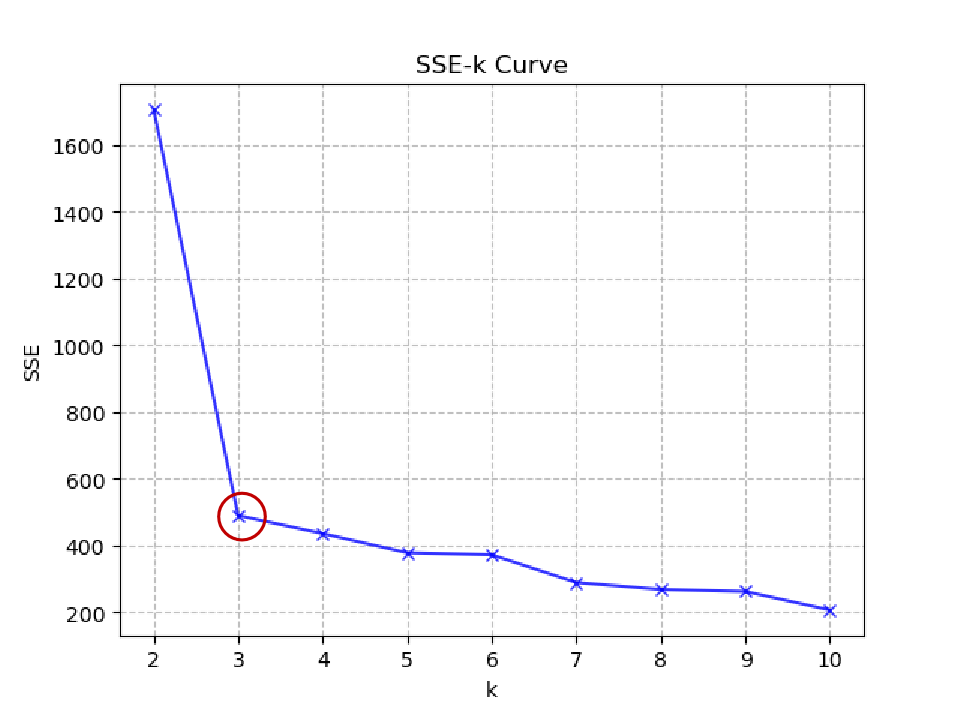
但由于此K-means算法对于初始化簇中心是敏感的，因此不同的初始化簇中心对手肘法会产生影响，因此在采用手肘法确定k值时，应当进行多次实验进行综合考虑。

8. 源码

import numpy as np
import random
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import datasets

def get_Euclidean_dist(vector1,vector2):
    dim=vector1.size
    temp=0
    for i in range(dim):
        temp+=(vector1[i]-vector2[i])**2
    dist=np.sqrt(temp)
    return dist

def init_centroids(samples,k):
    samples_num=samples.shape[0]
    samples_dim=samples.shape[1]
    rand_idx=random.sample(range(samples_num),k)
    centroids_init=np.zeros(shape=(k,samples_dim))
    for i in range(k):
        idx=rand_idx[i]
        centroids_init[i]=samples[idx].copy()
    return centroids_init

def get_closest_centroid_idx(sample,centroids):
    centroids_num=centroids.shape[0]
    closest_idx=0
    min_dist=get_Euclidean_dist(sample,centroids[0])
    for i in range(1,centroids_num):
        dist=get_Euclidean_dist(sample,centroids[i])
        if dist<min_dist:
            closest_idx=i
            min_dist=dist
    return closest_idx

def create_clusters(samples,centroids,k):
    clusters=[[] for i in range(k)]
    samples_num=samples.shape[0]
    for i in range(samples_num):
        closest_idx=get_closest_centroid_idx(samples[i],centroids)
        clusters[closest_idx].append(samples[i])
    return clusters

def update_centroids(clusters,centroids):
    clusters_num=len(clusters)
    centroids_update=np.zeros_like(centroids)
    for i in range(clusters_num):
        cluster=np.array(clusters[i])
        centroid=cluster.mean(axis=0)
        centroids_update[i]=centroid
    return centroids_update

def plot_clusters(clusters,sample_dim,centroids,iter):
    clusters_num=len(clusters)
    fig=plt.figure()
    if sample_dim==2:
        ax=fig.add_subplot()
    else:
        ax=fig.add_subplot(projection='3d')
    if sample_dim==2:
        for i in range(clusters_num):
            cluster=np.array(clusters[i])
            ax.scatter(cluster[:,0],cluster[:,1],edgecolors='k',marker='o',s=40,alpha=0.6)
        ax.scatter(centroids[:,0],centroids[:,1],edgecolors='r',marker='x',c='r',s=60)
        ax.set_title(f'Iter {iter}')
    else:
        for i in range(clusters_num):
            cluster=np.array(clusters[i])
            ax.scatter(cluster[:,0],cluster[:,1],cluster[:,2],edgecolors='k',marker='o',s=40,alpha=0.6)
        ax.scatter(centroids[:,0],centroids[:,1],centroids[:,2],edgecolors='r',marker='x',c='r',s=60)
        ax.set_title(f'Iter {iter}')
    plt.show()

def K_means_Algorithm(samples,k,max_iter):
    centroids=init_centroids(samples,k)
    sample_dim=samples.shape[1]
    for i in range(max_iter):
        clusters=create_clusters(samples,centroids,k)
        pre_centroids=centroids.copy()
        centroids=update_centroids(clusters,pre_centroids)
        diff=centroids-pre_centroids
        if sample_dim==2 or sample_dim==3:
            plot_clusters(clusters,sample_dim,centroids,i+1)
        if not diff.any():
            break

def elbow_method(samples,max_k):
    # 手肘法
    k_list=np.arange(2,max_k+1)
    SSE_list=[]
    for k in k_list:
        centroids=init_centroids(samples,k)
        while True:
            clusters=create_clusters(samples,centroids,k)
            pre_centroids=centroids.copy()
            centroids=update_centroids(clusters,pre_centroids)
            diff=centroids-pre_centroids
            if not diff.any():
                SSE=0
                for i in range(len(clusters)):
                    for sample in clusters[i]:
                        tmp=sample-centroids[i]
                        SSE=SSE+np.dot(tmp,tmp)
                SSE_list.append(SSE)
                break
    SSE_list=np.asarray(SSE_list)
    fig=plt.figure()
    plt.plot(k_list,SSE_list,marker='x',color='blue',alpha=0.8)
    plt.title('SSE-k Curve')
    plt.xlabel('k')
    plt.ylabel('SSE')
    plt.grid(ls='--',alpha=0.8)
    plt.show()

if __name__=="__main__":
    samples0,true_label0=datasets.make_blobs(n_samples=1000,
                                             n_features=2,
                                             centers=[[0,0],[2,2],[4,4]],
                                             cluster_std=0.5)

    # samples1,true_label1=datasets.make_blobs(n_samples=500,
    #                                          n_features=3,
    #                                          centers=[[-2,-2,-2],[0,0,0],[2,2,2]],
    #                                          cluster_std=0.6)
    #
    # samples2,true_label2=datasets.make_circles(n_samples=500,
    #                                            noise=0.1,
    #                                            factor=0.5)
    #
    # samples3,true_label3=datasets.make_moons(n_samples=500,noise=0.1)

    K_means_Algorithm(samples0,3,100)

    #elbow_method(samples0,10)