【离散数学】图论 第七章(8) 运输网络、流和割、Ford-Fulkerson定理

本文属于「离散数学」系列文章之一。这一系列着重于离散数学的学习和应用。由于内容随时可能发生更新变动，欢迎关注和收藏离散数学系列文章汇总目录一文以作备忘。此外，在本系列学习文章中，为了透彻理解数学知识，本人参考了诸多博客、教程、文档、书籍等资料。以下是本文的不完全参考目录，在后续学习中还会逐渐补充：

• （国外经典教材）离散数学及其应用 第八版 Discrete Mathematics and Its Applications Eighth Edition ，作者是 Kenneth H.Rosen ，袁崇义译，机械工业出版社
• 离散数学 第二版，武波等编著，西安电子科技大学出版社，2006年
• 离散数学 第三版，方世昌等编著，西安电子科技大学出版社，2013年
• （经典参考书及其题解）离散数学/离散数学——理论•分析•题解，左孝凌、李为鉴、刘永才编著，上海科学技术文献出版社
• 离散数学习题集：数理逻辑与集合论分册，耿素云；图论分册，耿素云；抽象代数分册， 张立昂。北京大学出版社

---

8. 运输网络

8.1 运输网络的定义

运输网络是对各类运输系统中 物资从起点 $s$ 出发、经过多个中转站点、到达终点 $t$ 这类现象的数学抽象，可以用有向图进行描述。

定义8.1 设 $G=⟨V,E,\omega ⟩$ 是一个连通 边赋权 有向 简单图，若 $G$ 中恰有一个入度为零的结点和一个出度为零的结点，则称 $G$ 为运输网络 transport network 。入度为零的结点称为源点 source ，出度为零的结点称为汇点 sink 。对于任一边 $e\in E$ 上的权值，$\omega (e)$ 称为 $e$ 的容量。

下图8.1中，源点 $s=a$ ，汇点 $t=f$ ，边 $⟨a,b⟩$ 的容量 $\omega (a,b)=4$ ，边 $⟨a,d⟩$ 的容量 $\omega (a,d)=5$ ，边 $⟨c,f⟩$ 的容量 $\omega (c,f)=4$ ，边 $⟨d,c⟩$ 的容量 $\omega (d,c)=2$ ，以此类推。对于这张图，我们可以把它认为是一个输油管道网络的有向图，原油在码头 $a$ 卸下并通过管道泵送到炼油厂 $f$ ，结点 $a,b,c,d,e$ 表示中间泵站，有向边表示输油管道、并标明了原油的流动方向，边上的数字表示该管道单位时间内的最大输油量。

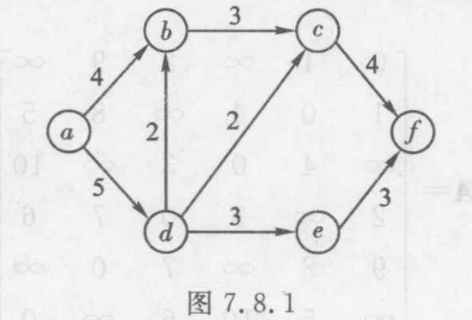
在运输网络中，人们关心的问题是求解最大运输量，公路铁路运输系统、供水供电系统、传送数据流的计算机网络等，都可以使用运输网络来建模。物资从源点到汇点的实际流通量，除了与每条边的容量相关外，还与每个结点的转运能力相关。

8.2 流

定义8.2.1 在运输网络 $G=⟨V,E,\omega ⟩$ 中，设 $\varphi$ 是从 $E$ 到非负实数集合上的一个函数，如果满足以下条件，则称 $\varphi$ 为该运输网络中的一个流：

• 任取 $⟨u,v⟩\in E$ ，$\varphi (u,v)\le \omega (u,v)$ ，即单位时间内每条边的流量不能超过边的容量；
• 源点 $s$ 和汇点 $t$ 满足 $$\sum _{⟨s,u⟩\in E}\varphi (s,u)=\sum _{⟨v,t⟩\in E}\varphi (v,t)$$ 即单位时间内源点的流入量等于汇点的流出量；
• 除源点 $s$ 和汇点 $t$ 以外，其余每一结点 $v$ 均满足 $$\sum _{⟨u,v⟩\in E}\varphi (u,v)=\sum _{⟨v,w⟩\in E}\varphi (v,w)$$
  即每个结点的流入量等于流出量

值 $\varphi (u,v)$ 称为流 $\varphi$ 在边 $⟨u,v⟩$ 的流量，而 ${\sum }_{⟨s,u⟩\in E}\varphi (s,u)$ 称为流 $\varphi$ 在整个运输网络 $G$ 的流量 value ，记为 ${\varphi }_G$ 。对于边 $⟨u,v⟩$ 来说，如果 $\varphi (u,v)=\omega (u,v)$ ，称边 $⟨u,v⟩$ 是饱和的；如果 $\varphi (u,v)<\omega (u,v)$ ，称边 $⟨u,v⟩$ 是非饱和的。

仍以8.1中的输油管道网络为例，第一个条件的含义是单位时间内每条管道的通油量不能超过管道的容量；第二个条件的含义是单位时间内泵送到炼油厂的总油量等于从码头卸下并输进管道的总油量；第三个条件的含义是每个中间泵站处油的流入量等于其流出量，即原油在这些中间泵站既无消耗也无补充。

下图8.2给出了图8.1所示运输网络的一个流。如果边 $e$ 的容量是 $x$ ，而流量是 $y$ ，则边 $e$ 上标记 $x,y$ 。例如边 $⟨a,b⟩$ 的标记为 $4,0$ ，表示其容量等于 $4$ 、当前流量等于 $0$ ；边 $⟨d,c⟩$ 的标记为 $2,1$ ，表示其容量等于 $2$ 、当前流量等于 $1$ ；边 $⟨b,c⟩$ 的标记为 $3,2$ ，表示其容量等于 $3$ 、当前流量等于 $2$ 。

一个运输网络中能承载多种流，其中流量值最大的流称为最大流 maximum flow。最大流也可能不止一个，即可能会有多个不同的流都具有最大流量。给定运输网络求其最大流，是一个很有现实意义的问题，可以用来确定怎样才能使网络的运输效率最高，即单位时间内网络中物资的运输量最大。

为了解决这个问题，先要引入割的概念和相关定理。

8.3 割

定义8.3.1 设图 $G=⟨V,E,\omega ⟩$ 是一个运输网络，$X\subset V$ ，记为 $\overline{X}=V-X$ 。若 $s\in X$ 且 $t\in \overline{X}$ ，则称集合 ( X , X ‾ ) = { ⟨ u , v ⟩   ∣   u ∈ X , v ∈ X ‾ , ⟨ u , v ⟩ ∈ E } (X, \overline X) = \{ \lang u, v\rang \ | \ u\in X, v \in \overline X, \lang u, v\rang \in E\} (X,X)={⟨u,v⟩ ∣ u∈X,v∈X,⟨u,v⟩∈E}

为运输网络 $G$ 的一个割，令 $$\omega (X,\overline{X})=\sum _{⟨u,v⟩\in (X,\overline{X})}\omega (u,v)$$

则称 $\omega (X,\overline{X})$ 为割 $(X,\overline{X})$ 的容量。

显然，对运输网络的一个割来说，每条从源点到汇点的有向路，至少要通过割中的一条边。

例1 图8.3.1中的虚线给出了图8.1所示运输网络的一个割，该割将结点集合分为 X = { a , b } X = \{a, b\} X={a,b} 和 X ‾ = { c , d , e , f } \overline X = \{c, d, e, f\} X={c,d,e,f} 。割 ( X , X ‾ ) = { ⟨ a , d ⟩ , ⟨ b , c ⟩ } (X, \overline X) = \{\lang a, d\rang , \lang b, c\rang\} (X,X)={⟨a,d⟩,⟨b,c⟩} ，该割的容量是 $\omega (X,\overline{X})=5+3=8$ 。

https://www.cxybb.com/article/aiweiluan5095/102214905

定理8.3.1 在运输网络中任意一个流的流量均小于等于该运输网络中任意一个割的容量。
证明：设 $G=⟨V,E,\omega ⟩$ 是一个运输网络，$\varphi$ 是该运输网络的任意一个流，$(X,\overline{X})$ 是该运输网络的任意一个割。对于源点 $s$ ，有：
$$\sum _{⟨s,u⟩\in E}\varphi (s,u)={\varphi }_G$$
对于 $X$ 中不是源点的结点 $p$ 均有：
$$\sum _{⟨u,v⟩\in E}\varphi (u,v)=\sum _{⟨v,w⟩\in E}\varphi (v,w)$$

由这两式可得：

下面举例说明这一定理的含义。如果从北京到上海的所有货物，都要经过武汉长江大桥或南京长江大桥，即使是用足这两座大桥的通行能力，从北京发往上海的单位时间内的货物量，也不能超过这两座大桥单位时间内货物的最大通行量。

考虑如图8.3.2(a)所示的一条路，这条路是图8.2.1所示的运输网络中的一条从源点 $s=a$ 到汇点 $t=f$ 的路。

定义8.3.2 设 $G=⟨V,E,\omega ⟩$ 是以 $s$ 为源点、以 $t$ 为汇点的运输网络，称结点序列 $s=v_0,v_1,\dots ,v_{n-1},v_n=t$ 为 $G$ 中的一条不考虑边方向的从 $s$ 到 $t$ 的道路。如下图8.3.2所示，若 $⟨v_i,v_{i+1}⟩\in E$ ，则称 $⟨v_i,v_{i+1}⟩$ 为一条前向边 forward edge ；若 $⟨v_{i+1},v_i⟩\in E$ ，则称 $⟨v_{i+1},v_i⟩$ 为一条后向边 backward edge 。

现实中，还有很多运输网络可能有多个源点和多个汇点。此时只需要在原运输网络中添加一个虚拟的源点 $s^{\prime }$ 和一个虚拟的汇点 $t^{\prime }$ ，再添加以虚源 $s^{\prime }$ 为起点、到原运输网络各个源点的有向边，容量均设置为 $+\infty$ ，添加以原运输网络各个汇点为起点、到虚汇 $t^{\prime }$ 的有向边，容量均设为 $+\infty$ ，即可将多源多汇问题转化为本节介绍的单源单汇问题。