1. 概念
粒子群优化算法(PSO:Particle swarm optimization) 是一种进化计算技术(evolutionary computation)。
源于对鸟群捕食的行为研究。粒子群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解.
PSO的优势:在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。
2. 算法
2.1 问题抽象
鸟被抽象为没有质量和体积的微粒(点),并延伸到N维空间,粒子i在N维空间的位置表示为矢量Xi=(x1,x2,…,xN),飞行速度表示为矢量Vi=(v1,v2,…,vN)。每个粒子都有一个由目标函数决定的适应值(fitness value),并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Xi。这个可以看作是粒子自己的飞行经验。除此之外,每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值),这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。2.2 更新规则
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中,粒子通过跟踪两个“极值”(pbest,gbest)来更新自己。在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置。
公式(1)的第一部分称为【记忆项】,表示上次速度大小和方向的影响;公式(1)的第二部分称为【自身认知项】,是从当前点指向粒子自身最好点的一个矢量,表示粒子的动作来源于自己经验的部分;公式(1)的第三部分称为【群体认知项】,是一个从当前点指向种群最好点的矢量,反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
以上面两个公式为基础,形成了PSO的标准形式。
公式(2)和 公式(3)被视为标准PSO算法。
2.3 标准PSO算法流程
标准PSO算法的流程:
1)初始化一群微粒(群体规模为N),包括随机位置和速度;
2)评价每个微粒的适应度;
3)对每个微粒,将其适应值与其经过的最好位置pbest作比较,如果较好,则将其作为当前的最好位置pbest;
4)对每个微粒,将其适应值与其经过的最好位置gbest作比较,如果较好,则将其作为当前的最好位置gbest;
5)根据公式(2)、(3)调整微粒速度和位置;
6)未达到结束条件则转第2)步。
迭代终止条件根据具体问题一般选为最大迭代次数Gk或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。
公式(2)和(3)中pbest和gbest分别表示微粒群的局部和全局最优位置。
当C1=0时,则粒子没有了认知能力,变为只有社会的模型(social-only):
被称为全局PSO算法。粒子有扩展搜索空间的能力,具有较快的收敛速度,但由于缺少局部搜索,对于复杂问题
比标准PSO 更易陷入局部最优。
当C2=0时,则粒子之间没有社会信息,模型变为只有认知(cognition-only)模型:
被称为局部PSO算法。由于个体之间没有信息的交流,整个群体相当于多个粒子进行盲目的随机搜索,收敛速度慢,因而得到最优解的可能性小。
2.4 参数分析
参数:群体规模N,惯性因子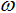
群体规模N:一般取20~40,对较难或特定类别的问题可以取到100~200。
最大速度Vmax:决定当前位置与最好位置之间的区域的分辨率(或精度)。如果太快,则粒子有可能越过极小点;如果太慢,则粒子不能在局部极小点之外进行足够的探索,会陷入到局部极值区域内。这种限制可以达到防止计算溢出、决定问题空间搜索的粒度的目的。
权重因子:包括惯性因子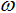
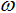
参数设置:
1) 如果令c1=c2=0,粒子将一直以当前速度的飞行,直到边界。很难找到最优解。
2) 如果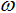
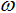
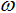
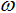
3) 通常设c1=c2=2。Suganthan的实验表明:c1和c2为常数时可以得到较好的解,但不一定必须等于2。Clerc引入收敛因子(constriction factor) K来保证收敛性。
通常取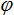
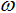
例。
恰当的选取算法的参数值可以改善算法的性能。
3. PSO与其它算法的比较
3.1 遗传算法和PSO的比较
1)共性:(1) 都属于仿生算法。
(2) 都属于全局优化方法。
(3) 都属于随机搜索算法。
(4) 都隐含并行性。
(5) 根据个体的适配信息进行搜索,因此不受函数约束条件的限制,如连续性、可导性等。
(6) 对高维复杂问题,往往会遇到早熟收敛和收敛 性能差的缺点,都无法保证收敛到最优点。
2)差异:
(1) PSO有记忆,好的解的知识所有粒子都保 存,而GA(Genetic Algorithm),以前的知识随着种群的改变被改变。
(2) PSO中的粒子仅仅通过当前搜索到最优点进行共享信息,所以很大程度上这是一种单共享项信息机制。而GA中,染色体之间相互共享信息,使得整个种群都向最优区域移动。
(3) GA的编码技术和遗传操作比较简单,而PSO相对于GA,没有交叉和变异操作,粒子只是通过内部速度进行更新,因此原理更简单、参数更少、实现更容易。
(4) 应用于人工神经网络(ANN)
GA可以用来研究NN的三个方面:网络连接权重、网络结构、学习算法。优势在于可处理传统方法不能处理的问题,例如不可导的节点传递函数或没有梯度信息。
GA缺点:在某些问题上性能不是特别好;网络权重的编码和遗传算子的选择有时较麻烦。
已有利用PSO来进行神经网络训练。研究表明PSO是一种很有潜力的神经网络算法。速度较快且有较好的结果。且没有遗传算法碰到的问题。


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








