昨晚和秦淮说到一道让他老人家纠结了近半年的离散数学真题。由于昨晚笔者发烧感冒,脑子有些反应滞后,忙到凌晨,身体实在吃不消就没有整理,今天给出个整理中的结论吧(个人分析,仅供参考):
来看题:
6.有向图G=<{1,2,,3,…,n},{<i,j>|当i,j 同奇偶时且i>j}或{<i,j>|当i,j 不同奇偶时且i<j}>问:
(1)G 是竞赛图吗?为什么?
(2)G 是欧拉图吗?为什么?
(3)G 是哈密顿图吗?为什么?
(4)G 是强连通图吗?为什么?
(5)G 是可平面图吗?为什么?
答:(1)是竞赛图。因为i和j可以取遍{1,2,……n},又根据题意知道每条边位单向边,且每两个顶点都有一条边。根据竞赛图的定义知G是竞赛图
下面来看相关知识点的分析:

(a) (b) (c)
无向完全图===>有向完全图===>4阶竞赛图(单边单向)
每两个顶点间 去掉两个顶点
建立2个反向的边 间一个方向的边
----------------------------------------------------------------------------------------------------------
6.有向图G=<{1,2,,3,…,n},{<i,j>|当i,j 同奇偶时且i>j}或{<i,j>|当i,j 不同奇偶时且i<j}>问:
(2)G 是欧拉图吗?为什么?
答:需要分情况讨论(n为偶数时,G不是欧拉图;n为奇数时,G为欧拉图):
一.当n为偶数时:
任取一顶点v,则根据题意,有度: , v的出度
, v的出度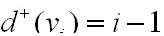 , 入度
, 入度 ,根据有向连通图是否欧拉图的判定定理知,若有向图G为欧拉图则对任意顶点v有
,根据有向连通图是否欧拉图的判定定理知,若有向图G为欧拉图则对任意顶点v有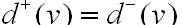 , 矛盾,则G在n为偶数时不时欧拉图。
, 矛盾,则G在n为偶数时不时欧拉图。
-------------------->这里的入度出度是这么归纳出来的:如下:
对任意vi取G中偶数,则,
偶连偶(<i,j>,i<j):使vi与G中所有vj(j取遍G中所有奇数,且j不等于i),
 ,
,
这是因为偶偶顶点在G中是间隔出现的,偶顶点在G中有n/2个,vi要与其他(n/2)-1个偶顶点相连。
 ,
,
这是因为vi的出度为:|{小于i的所有偶数}|-1=(i/2)-1.
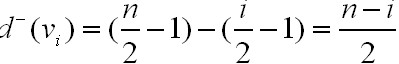 ,
,
这是因为 vi的入度为:vi的度-vi的出度.
=============>
偶连奇(<i,j>,i>j):使vi与G中所有vj(j取遍G中所有奇数,且j不等于i),
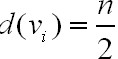 ,
,
这是因为G中有n/2个奇顶点,任一vi与所有奇顶点相连。
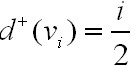 ,
,
这是因为 vi的出度为:|{小于i的所有奇数}|=i/2
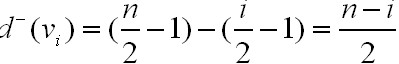
这是因为 vi的入度为:vi的度-vi的出度.则此时有:
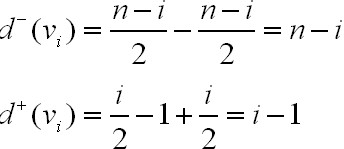
~~~~~~>同理也可归纳对任意vi,i取G中奇数的情况(结果是一样的),
奇连奇:


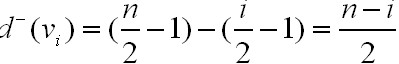
奇连偶:
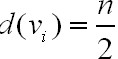
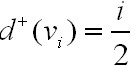
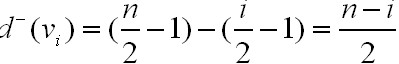
则此时有:
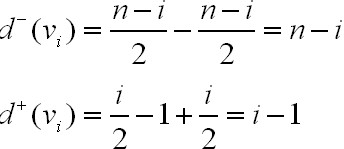
那么也就是在G中有:
 即:
即:
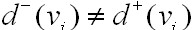 .即知有向图G不是欧拉图得证。
.即知有向图G不是欧拉图得证。
二,n为奇数时,类似可以讨论:
可以得到:
 ,
,
所以当n为奇数时,有向图G为欧拉图,得证。
---------------------------------------------------------------
6.有向图G=<{1,2,,3,…,n},{<i,j>|当i,j 同奇偶时且i>j}或{<i,j>|当i,j 不同奇偶时且i<j}>问:
(3)G 是哈密顿图吗?为什么?
答:是哈密顿图。因为G为n阶竞赛图,则G中存在哈密顿通路(定理8.9),且有i,j取遍G中所以顶点,且每个顶点都是相连且有通路的.
----------------------------------------------------------------
6.有向图G=<{1,2,,3,…,n},{<i,j>|当i,j 同奇偶时且i>j}或{<i,j>|当i,j 不同奇偶时且i<j}>问:
(4)G 是强连通图吗?为什么?
答:是。因为有向图G是哈密顿图,必满足到所有顶点可达。(有定理8.10:强连通竞赛图式哈密顿图)
------------------------------------------------------------------
(5)G 是可平面图吗?为什么?
答:n>4时,不可平面化。因为根据定理11.10:当G为n(n=3或n>3)阶m条边的简单平面图,则m<=3n-6.此题中m=n(n-1)/2,那么建立不等式可解得,n=3,4.当n=1,2时也成立。所以所当n>5时不是可平面图。






















 4405
4405

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








