雷达原理 | 用MATLAB信号处理是如何解算目标的距离和速度信息的？

转载：https://zhuanlan.zhihu.com/p/422798513
大家好！我是喜欢把问题研究明白的调皮哥。

欢迎前来学习毫米波雷达基本原理。本节课将讲的是毫米波雷达利用MATLAB进行信号处理如何解算目标的距离和速度信息。
一、
很多同学在看完雷达原理的基本公式之后，大致上能够明白雷达测距和测速的基本原理，但是到了真正利用MATLAB做信号处理的时候，可能不是很清楚，为什么经过两次FFT（距离维、速度维）这么做就能够得到目标的距离和速度，其背后的实质物理含义是什么？今天带着这个疑问，我把这个问题研究一下，希望能够从最底层的原理给大家解释清楚，并让大家明白到底MATLAB是如何计算出目标得到距离和速度的。

1. 发射信号的模型可以假设，线性调频连续波（LFMCW） 雷达发射波形的信号形式为调频连续锯齿波，线性调频的含义即调制信号频率随时间线性变化。从时域上看，是一个频率随时间线性变化的波形；从频域上看， 发射信号的频率与时间成正比， 如图1-1所示。

图1-1 LFMCW锯齿波模型

由此，可以将LFMCW的发射信号模型用下面公式表示：

其中，发射信号扫频带宽(频段宽度)为 B，发射时宽(信号持续的时间)为T，即调频斜率为 B/T，记为u 。

所以，单周期 LFMCW 雷达发射信号模型的相位可以写成如下形式：

2. 静止情况下测距

假设静止的目标距离雷达的距离为R，电磁波在空气中传输速度为c，则接受天线接受到的信号比发射的信号延迟τ=2R/c，所以理想情况下接受天线接收到的目标回波信号模型如下所示：

由上述公式可知，回波信号具有和发射信号同样的信号形式，相对于发射信号在时间上有固定延时τ，故而回波信号的相位可以表式为：

将接收到回波信号Sr(t)和发射信号St(t)进行混频，并经过低通滤波器后就可以得到一个单一频率的正弦波信号，如图中黑色的“IF signal”便是中频信号的频率，如图1-2所示。

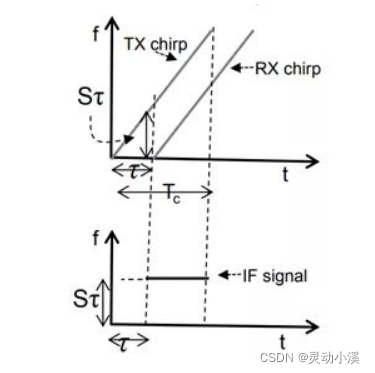
图1-2 混频

根据公式推导， 可以得到差频信号的相位表达式为：

此时可以很明显地看出，发射信号和单目标的回波信号的频率差为一个单频信号。根据上式，可以得到中频信号频率fm，如下所示：

对中频信号进行 ADC 采样， 然后做 FFT 提取信号的频率信息， 假设 FFT 得到频谱的谱峰值对应的频率为fm ， 则目标的距离信息可以表示如下：

3. 运动目标情况下测距

假设，在电磁波的覆盖区域中，某一目标在t0时刻距离发射天线为R0，以径向v远离天线，以远离天线为正方向，至于为什么后续文章会解释）。那么接受到目标的回波信号模型公式依旧与单目标一致，如下所示：

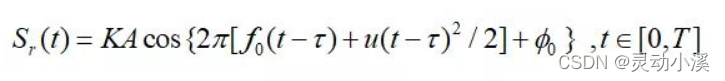
但是，τ有所改变，如下所示：

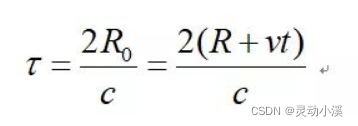
此时，通过混频后得到中频信号的相位如下所示：

代入τ后的等式变为：

很显然，根据上述公式可知，对于运动目标的信号的中频信号依然是一个线性调频信号，所以信号的调频斜率Um，载频fm，初相ϕm分别如下：

因为光速c等于3*10^8m/s，所以忽略c的平方项，则中频信号的时宽带宽积Dm为:

其中，Bm中频信号的调频带宽，为D为发射信号时宽带宽积。

上述公式可以表明，即使目标在几百米每秒的高速运动情况下，中频信号的时宽带宽积仅有原来的10^-6 倍，在毫米波雷达发射极大时宽带宽积（10^{6）的信号情况下，中频信号Dm的数量级也只有10}0 。

因此，可近似认为回波差拍信号是一单频信号，通过频谱分析（FFT）即能得到其中心频率。所以TI的官方文档中，将中频信号近似地写成：

并说明了这个公式是近似值，其中f0等效fm。TI官方给出的中频信号中心频率和相位的公式如下：
其中，d为目标距雷达的距离。

下面由上述推导的公式来证明，为什么最终会是这个简单的公式呢？将下面的公式去掉光速的平方项，做近似。

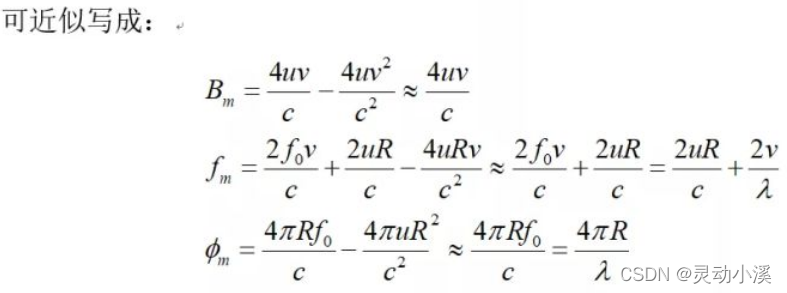
如果忽略多普勒频率对对中频信号频率的影响，则

关于上述TI官方给出的中频信号的近似值，就是这么得到的。近似公式忽略 IF 信号的频率与物体速度的依赖关系。在快速 FMCW 雷达中，其影响通常非常小，且在处理完成多普勒 FFT 后，即可轻松对其进行进一步校正，这就是多普勒相位补偿。

二、

假设单个扫描周期 ADC采样点数为 N， 采样频率为Fs， 式中 n 为 FFT 谱峰对应的频点， 根据 T、 Fs、 N 之间的关系，距离与频率关系的公式可进一步化简为：

式中，c/2B为雷达的距离分辨率ΔR， 可见中频信号的 FFT 谱峰对应的频点，即目标距离门号，乘以距离分辨率就可得到目标的距离。

上述公式就是在用MATLAB计算目标的距离的时候，我们通常得到的是点的序号（距离门号），而不是直接得到目标的距离，因此需要通过这个公式将距离门号转换成目标真实的距离。

在MATLAB中，对于距离维做FFT，目的就是找出中频频率峰值和频点，然后根据峰值所在的距离门号，解算出目标的距离，具体如图2-1所示。

图2-1 距离解算前

例如，上述数据的雷达发射信号的真实带宽：68*(256/5500)=3165MHz;真实距离分辨率：ΔR = C/2B=0.048m，所以对应点目标的距离为：

R = (n-1)ΔR = 114*0.047=5.47m,MATLAB起始点是从1开始的，所以是n-1。即可得到距离解算的结果，如图2-2所示。

图2-2 距离解算后

至此，我们推导并论证了线性调频连续波测距原理的来龙去脉，大概讲清楚了从信号发射、回波信号、混频、低通滤波、中频信号，到距离估计的整个脉络，同时梳理清楚了由TI官方给出的公式近似值的背后隐藏的一些理论，并展现了我们为什么要这么做，背后的含义是什么的解释。最后也为大家推导的公式，为后续做相位补偿提供了理论依据。
三、
之前的文章写过线性调频连续波测速的基本原理，是利用多个脉冲之间的相位差，然后做FFT得到的。
重现上述推导的公式如下：

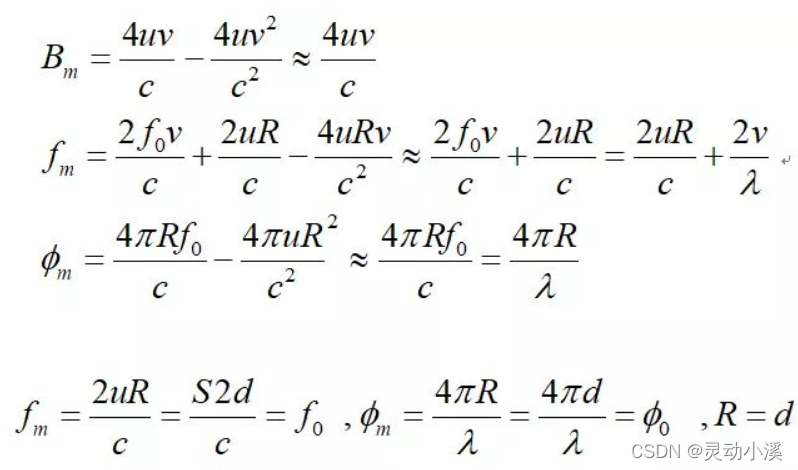
对于两个相邻周期的信号，由于周期间隔时间Tc较短，距离分辨率有限，两个周期内距离维FFT谱中的峰值位置几乎没有发生变化，但是由于相位比距离更加敏感，即周期间微小的距离变化会引起中频信号的初相的变化。

由傅里叶变换特性，信号的初相体现在峰值处的复数值对应的相位，计算相邻周期的相位差，即可得到目标的速度：

其中，两个脉冲相邻的微小距离变化为v*Tc，所以两个脉冲间的速度为：

推广到多个脉冲，如128个，那么相位的变化是呈周期性的，速度维度做128点FFT后的峰值就是相位差，即获取速度对应的峰值和频点再通过解算便可获得目标的速度，这个过程就是速度维FFT。接下来进行速度解算。上述公式经过推导可以变为：

其中，相位的最大值为2π。由此，速度的解算依赖于速度分辨率和速度门号，速度门号即为速度维FFT之后拿到的峰值所对应的下标（频点）。例如图3-1所示，为速度解算过程。

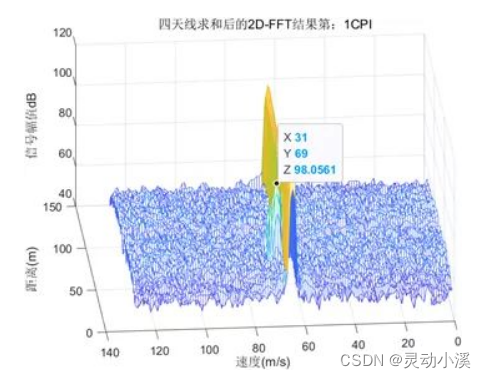
图3-1 速度解算前

其中，X轴是距离，Y轴是速度，上图X=31，Y=69；距离分辨率为0.48m，速度分辨率为0.083m/s。

所以根据上述推导的公式，n=31-1=30；R=ΔRn =1.41m，速度分根据目标运动方向分为正负，这里一共是128个脉冲，零速通道是第64个脉冲，所以69为正速通道，具体速度通道号为Y=69-64=5；n=5-1=4；v =Δvn=0.33m/s，如图3-2所示。

图3-2 速度解算后

至此，关于目标的距离估计、速度估计的解算方法解释完毕！