4.设A是方阵,如有矩阵关系式AB=AC,则必有( d )
A. A=0 B.BC时A=0
C. A=0时B=C D.|A|=0时B=C
10.设A是一个n(≥3)阶方阵,下列陈述中正确的是( b )
A.如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量
B.如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值
C.A的2个不同的特征值可以有同一个特征向量
D.如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关
12.设A是正交矩阵,则下列结论错误的是( b )
A.|A|2必为1 B.|A|必为1
C.A-1=AT D.A的行(列)向量组是正交单位向量组
13.设A是实对称矩阵,C是实可逆矩阵,B=CTAC.则( d )
A.A与B相似
B. A与B不等价
C. A与B有相同的特征值
D. A与B合同
14.下列矩阵中是正定矩阵的为( c )
A. B.
C. D.
21.设向量α、β的长度依次为2和3,则向量α+β与α-β的内积(α+β,α-β)= -5 .
24.设实二次型f(x1,x2,x3,x4,x5)的秩为4,正惯性指数为3,则其规范形为 x1^2 + x2^2 + x3 ^2 - x4^2 .
[x,y]^2 ≤ [x,x]*[y,y] 设x=(x1,x2...xn) y=(y1,y2...yn) 则[x,y]^2=(x1y1+x2y2+...xnyn)^2 [x,x]*[y,y]=(x1^2+x2^2+...xn^2)(y1^2+y2^2+...+yn^2) 首先构造方程(x1z-y1)^2+(x2z-y2)^2+...+(xnz-yn)^2=0 z是未知数,其他的是参数。 我们知道这个方程最多只有一个解,这个方程可以改成 (x1^2+x2^2+...xn^2)z^2-2*=(x1y1+x2y2+...xnyn)*z+(y1^2+y2^2+...+yn^2)=0 那么它的Δ<=0 也就是说=4(x1y1+x2y2+...xnyn)^2-4(x1^2+x2^2+...xn^2)(y1^2+y2^2+...+yn^2)<=0 则[x,y]^2 ≤ [x,x]*[y,y]
格拉姆-施密特正交化 的证明
http://blog.sina.com.cn/s/blog_495b66300100mrho.html
调和平均<=几何平均<=算术平均<=平方平均 的证明:
即1/(1/a+1/b)<=根号(ab)<=(a+b)/2<=根号[(a^2+b^2)/2]
调和平均=1/(1/a+1/b)
几何平均=根号(ab)
算术平均=(a+b)/2
平方平均=根号[(a^2+b^2)/2]
已知x为锐角,用图的方法来解答你第一个不等式。
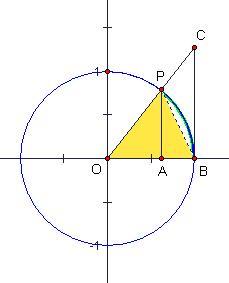
正弦线AP=sinx,正切线BC=tanx, 弧BP=x
明显就能看出AP<BP<BC 也就是、sinx<x<tanx
第二个不等式由(sinx)^2+(cosx)^2=1 推出,
由于sinx<=1 cosx<=1 且不可能同时满足sinx=1 cosx=1,所以(sinx)^3=sinx*(sinx)^2<(sinx)^2
(cosx)^3=cosx*(cosx)^2<(cosx)^2 必然满足其一,所以(sinx)^3+(cosx)^3<(sinx)^2+(cosx)^2=1

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








