神经网络的前向与反向传播过程详解

ningzhao

已于 2024-04-01 09:25:44 修改

阅读量957

点赞数 7

文章标签：神经网络人工智能机器学习

于 2023-12-08 14:50:35 首次发布

本文链接：https://blog.csdn.net/ningzhao/article/details/134868983

版权

一、神经网络的前向与反向传播过程详解

我们这里以最简单的神经网络为例说明。有三层网络，一个输入层，一个隐藏层，一个输出层，每层有2个神经元。

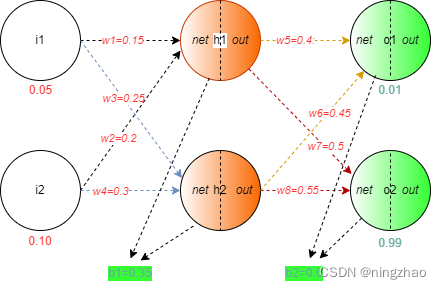
如图中所示:i1,i2为两个输入神经元，h1,h2为隐藏层两个神经元，o1,o2为两个输出神经元。

其中i1,i2两个输入值分别为0.05,0.10,真实输出值为0.01与0.99，w1-w8为权重值，是网络要学习的参数。b1,b2是偏置值。

1.前向传播（从输入层--->隐藏层-->输出层）

从输入层到隐藏层

$Net_{h1}=w1*i1 + w2*i2 +b1*1 \\ =0.15*0.05 + 0.20*0.10 + 0.35*1 \\=0.3775$

在这里激活函数使用逻辑函数

$Out_{h1}=\frac{1}{1+ e^{-Net_{h1}}} \\=\frac{1}{1+e^{-0.3775}} \\=0.5932699921071872$

同理，计算隐藏层的第二个神经元:

$Net_{h2}=w3*i1 + w4*i2 +b1*1 \\ =0.25*0.05 + 0.30*0.10 + 0.35*1 \\=0.3925$

$Out_{h2}=\frac{1}{1+ e^{-Net_{h2}}} \\=\frac{1}{1+e^{-0.3925}} \\=0.596884378259767$

从隐藏层到输出层

$Net_{o1}=w5*Out_{h1} + w6*Out_{h2} +b2*1 \\ =0.4*0.5932699921071872 + 0.45*0.596884378259767 + 0.6*1 \\=1.1059054$

$Out_{o1}=\frac{1}{1+ e^{-Net_{01}}} \\=\frac{1}{1+e^{-1.1059054}} \\=0.7513649636166884$

$Net_{o2}=w7*Out_{h1} + w8*Out_{h2} +b2*1 \\ =0.5*0.5932699921071872 + 0.55*0.596884378259767 + 0.6*1 \\=1.224921315$

$Out_{o2}=\frac{1}{1+ e^{-Net_{02}}} \\=\frac{1}{1+e^{-1.224921315}} \\=0.7729284496841369$

2.计算损失（损失函数使用MSE）

$\iota =\sum \frac{1}{2}\left ( target-output \right )^{2}$

这里的targt是真实值，output为计算值.这里的1/2是为了简化计算。

$E_{o1}=\sum \frac{1}{2}\left ( target_{o1}-output_{o1} \right )^{2}\\= \frac{1}{2}\left ( 0.01- 0.7513649636166884\right )^{2}\\=0.27481100463918684$

$E_{o2}=\sum \frac{1}{2}\left ( target_{o2}-output_{o2} \right )^{2}\\= \frac{1}{2}\left ( 0.99- 0.7729284496841369\right )^{2}\\=0.023560028978266145$

$E_{total}=E_{O1} +E_{O2}\\=0.27481100463918684+0.023560028978266145\\=0.298371033617453$

3.反向传播（从输出层-->隐藏层-->输入层）

反向传播的目的是更新所有权重值，使得每个输出神经元与整个网络的损失最小(即真实值与预测值最接近)

输出层

计算梯度

首先让我们来看w5的改变对网络损失的影响，即求偏导:

$\frac{\partial E_{total}}{\partial w_{5}}$ , 也可以叫做求关于 $w_{5}$ 的梯度。

使用链式法则可得：

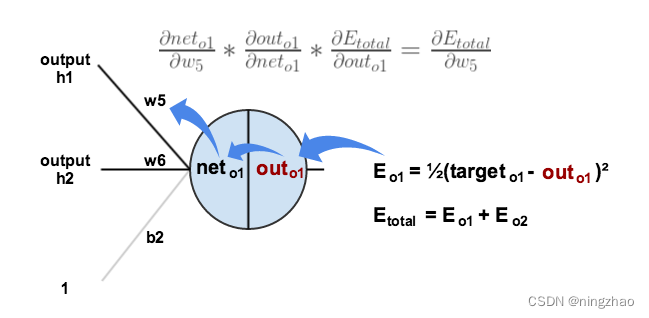
$\frac{\partial E_{total}}{\partial w_{5}}=\frac{\partial E_{total}}{\partial Out_{o1}}*\frac{\partial Out_{o1}}{\partial Net_{o1}} *\frac{\partial Net_{o1}}{\partial w_{5}}$

我们需要计算出这个方程中每一部分。

$E_{total}=E_{O1}+E_{O2}\\=\frac{1}{2}\left ( target_{o1} - out_{o1} \right )^{2} + \frac{1}{2}\left ( target_{o2} - out_{o2} \right )^{2}$

$\frac{\partial E_{total}}{\partial Out_{o1}}=2*\frac{1}{2}\left ( target_{o1} - out_{o1} \right )^{2-1} *{\left ( target_{o1} - out_{o1} \right )}' + \frac{1}{2}\left ( target_{o2} - out_{o2} \right )^{2}\\=2*\frac{1}{2}\left ( target_{o1} - out_{o1} \right )^{2-1} *-1 + \frac{1}{2}\left ( target_{o2} - out_{o2} \right )^{2}\\=2*\frac{1}{2}\left ( target_{o1} - out_{o1} \right )*-1 +0\\=-\left ( target_{o1} - out_{o1} \right )\\=-(0.01-0.7513649636166884)\\=0.7413649636$

$Out_{o1}=\frac{1}{1+ e^{-Net_{o1}}}$

逻辑函数 $\delta$ 的导数是 $\delta *\left ( 1-\delta \right )$

$\frac{\partial Out_{o1} }{\partial Net_{o1}}=Out_{o1} \, * \, \left ( 1-Out_{o1} \right )=0.7513649636166884 * \left ( 1-0.7513649636166884 \right )\\=0.18681565506598094$

$Net_{o1}=w5*Out_{h1} + w6*Out_{h2} +b2*1$

$\frac{\partial Net_{o1}}{\partial w_{5}}=Out_{h1} + 0 + 0=0.5932699921071872$

汇总

$\frac{\partial E_{total}}{\partial w_{5}}=\frac{\partial E_{total}}{\partial Out_{o1}}*\frac{\partial Out_{o1}}{\partial Net_{o1}} *\frac{\partial Net_{o1}}{\partial w_{5}}=0.7413649636 *0.18681565506598094 *0.5932699921071872\\=0.08216705224532783$

至此我们求得了关于 $W_{5}$ 的梯度。

更新权重

使用梯度下降法更新权重值

$W_{5}^{+}=W_{5}-\eta *\frac{\partial E_{total}}{\partial w_{5}}\\=0.4-0.5*0.08216705224532783=0.3589164738773361$

同理我们可以计算出 $W_{6}^{+},W_{7}^{+},W_{8}^{+}$ 的值，这里不再一一列举。

$\eta$ 表示学习率是超参数,这里设置为0.5。

隐藏层

在这里我们继续计算该层的权重参数 $W_{1},W_{2},W_{3},W_{4}$ 的新值。

计算梯度

首先我们看W1的改变对整个损失的影响。

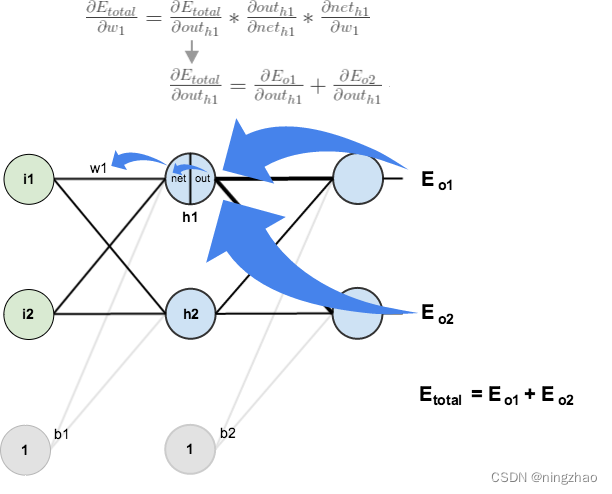
$\frac{\partial E_{total}}{\partial w_{1}}=\frac{\partial E_{total}}{\partial Out_{h1}}*\frac{\partial Out_{h1}}{\partial Net_{h1}} *\frac{\partial Net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial Out_{h1}}=\frac{\partial E_{o1}}{\partial Out_{h1}} + \frac{\partial E_{o2}}{\partial Out_{h1}}$

我们先求等式右边的第一项，依据链式法则：

$\frac{\partial E_{o1}}{\partial Out_{h1}}=\frac{\partial E_{o1}}{\partial Out_{o1}} * \frac{\partial Out_{o1}}{\partial Net_{o1}} * \frac{\partial Net_{o1}}{\partial Out_{h1}}$

$E_{o1}=\frac{1}{2}\left ( target_{o1} - out_{o1} \right )^{2}$

$\frac{\partial E_{o1}}{\partial Out_{o1}}=2*\frac{1}{2}\left ( target_{o1} - out_{o1} \right )^{2-1} *{\left ( target_{o1} - out_{o1} \right )}'\\=-\left ( target_{o1} - out_{o1} \right )=0.7413649636$

$\frac{\partial Out_{o1} }{\partial Net_{o1}}=Out_{o1} \, * \, \left ( 1-Out_{o1} \right )=0.7513649636166884 * \left ( 1-0.7513649636166884 \right )\\=0.18681565506598094$

$Net_{o1}=w_{5} * Out_{h1} + w_{6} * Out_{h2} + b_{2}*1$

$\frac{\partial Net_{o1}}{\partial Out_{h1}}=w_{5} + 0 + 0$

$\frac{\partial E_{o1}}{\partial Out_{h1}}=0.7413649636 *0.18681565506598094*0.4=0.05539943252716045$

接下来求：

$\frac{\partial E_{o2}}{\partial Out_{h1}}= \frac{\partial E_{o2}}{\partial Out_{o2}}* \frac{\partial Out_{o2}}{\partial Net_{o2}} * \frac{\partial Net_{o2}}{\partial Out_{h1}}$

$E_{o2}=\frac{1}{2}\left ( target_{o2} - out_{o2} \right )^{2}$

$\frac{\partial E_{o2}}{\partial Out_{o2}}=2*\frac{1}{2}\left ( target_{o2} - out_{o2} \right )^{2-1} *{\left ( target_{o2} - out_{o2} \right )}'\\=-\left ( target_{o2} - out_{o2} \right )= 0.7729284496841369-0.99\\=-0.21707155031586312$

$\frac{\partial Out_{o2} }{\partial Net_{o2}}=Out_{o2} \, * \, \left ( 1-Out_{o2} \right )=0.7729284496841369 * \left ( 1-0.7729284496841369 \right )\\= 0.17551006135301356$

$Net_{o2}=w_{7} * Out_{h1} + w_{8} * Out_{h2} + b_{2}*1$

$\frac{\partial Net_{o2}}{\partial Out_{h1}} =w_{7} + 0 + 0$

$\frac{\partial E_{o2}}{\partial Out_{h1}}=-0.21707155031586312 *0.17551006135301356*0.5\\=-0.019049120556965452$

$\frac{\partial E_{total}}{\partial Out_{h1}}=\frac{\partial E_{o1}}{\partial Out_{h1}} + \frac{\partial E_{o2}}{\partial Out_{h1}}\\=0.05539943252716045-0.019049120556965452\\=0.036350311970195004$

$Out_{h1}=\frac{1}{1+ e^{-Net_{h1}}}$

$\frac{\partial Out_{h1} }{\partial Net_{h1}}=Out_{h1} \, * \, \left ( 1-Out_{h1} \right ) =0.5932699921071872 * \left ( 1-0.5932699921071872 \right )\\=0.24130070857232525$

$Net_{h1}=w1*i_{1} + w2*i_{2} +b1*1$

$\frac{\partial Net_{h1}}{\partial w_{1}}=i_{1} + 0 + 0=0.05$

$\frac{\partial E_{total}}{\partial w_{1}}=\frac{\partial E_{total}}{\partial Out_{h1}}*\frac{\partial Out_{h1}}{\partial Net_{h1}} *\frac{\partial Net_{h1}}{\partial w_{1}}\\=0.036350311970195004*0.24130070857232525*0.05\\=0.00043856780176165653$

更新权重

使用梯度下降法更新权重值

$W_{1}^{+}=W_{1}-\eta *\frac{\partial E_{total}}{\partial w_{5}}\\=0.15-0.5*0.00043856780176165653=0.14978071609911917$

同理我们可以计算出 $W_{2}^{+},W_{3}^{+},W_{4}^{+}$ 的值，这里不再一一列举。

$\eta$ 表示学习率是超参数,这里设置为0.5。

最终我们使用同样的方法更新所有权重参数值。

参考：

A Step by Step Backpropagation Example | Matt Mazur

ningzhao

关注

7
点赞
踩
7

收藏

觉得还不错? 一键收藏
0
评论
神经网络的前向与反向传播过程详解

我们这里以最简单的神经网络为例说明。有三层网络，一个输入层，一个隐藏层，一个输出层，每层有2个神经元。如图中所示:i1,i2为两个输入神经元，h1,h2为隐藏层两个神经元，o1,o2为两个输出神经元。其中i1,i2两个输入值分别为0.05,0.10,真实输出值为0.01与0.99，w1-w8为权重值，是网络要学习的参数。b1,b2是偏置值。
复制链接

扫一扫