前提及说明
第一次遇见矩阵求导,大多数人都是一头雾水,而搜了维基百科看也还是云里雾里,一堆的名词和一堆的表格到底都是什么呢?这里总结了我个人的学习经验,并且通过一个例子可以让你感受如何进行矩阵求导,下次再遇到需要进行矩阵求导的地方就不会措手不及。
在进行概念的解说之前,首先大家需要先知道下面的这个前提:
前提: 若 x 为向量,则默认
x 为列向量, xT 为行向量
布局的概念
布局简单地理解就是分子 y 、分母
- 分子布局(Numerator-layout): 分子为 y 或者分母为
xT (即,分子为列向量或者分母为行向量) - 分母布局(Denominator-layout): 分子为 yT 或者分母为 x (即,分子为行向量或者分母为列向量)
为了更加深刻地理解两种布局的特点和区别,下面是从维基百科中布局部分拿来的例子:
分子布局
标量/向量:
(分母的向量为行向量)
向量/标量:
(分子的向量为列向量)
向量/向量:
(分子为列向量横向平铺,分母为行向量纵向平铺)
标量/矩阵:
(注意这个矩阵部分是转置的,而下面的分母布局是非转置的)
矩阵/标量:
分母布局
标量/向量:
(分母的向量为列向量)
向量/标量:
(分子的向量为行向量)
向量/向量:
(分子为行向量纵向平铺,分母为列向量横向平铺)
标量/矩阵:
(矩阵部分为原始矩阵)
一个求导的例子
问题
说明: y、w 为列向量, X 为矩阵
式子演化
看到这个例子不要急着去查表求导,先看看它的形式,是








 这篇博客介绍了矩阵求导的基本概念,包括分子布局和分母布局,并通过一个具体的求导例子详细解释了如何进行矩阵求导,帮助读者更好地理解和应用矩阵求导。
这篇博客介绍了矩阵求导的基本概念,包括分子布局和分母布局,并通过一个具体的求导例子详细解释了如何进行矩阵求导,帮助读者更好地理解和应用矩阵求导。
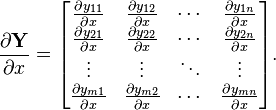
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5012
5012

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








