目录
一、点云配准概念
由于三维扫描测量设备受测量方式的限制和被测物体集合形状的限制,一次只能扫描被测物体有限范围的点云数据,这需要在多个视角下进行多次扫描,然而每个视角下得到点云数据都具有独立的坐标系,无法直接进行拼接。于是需要通过对每个视角下获取点云进行坐标转换,统一到全局坐标系下。具体流程是通过一个点集(目标)中的每一个点与另一个点集(原始点集)中的对应点的相互关系来实现点集与点集坐标系之间的转换,实现配准。
具体实现步骤:
(1)首先从两片点云数据中按照同样的关键点选取标准,提取关键点 ;
(2)对选择的所有关键点分别计算其特征描述子;
(3)结合特征描述子在两个数据集中的坐标的位置,以两者之间特征和位置的相似度为基础,来估计它们的对应关系,初步估计对应点对;
(4)假定数据是有噪声的,除去对配准有影响的错误的点对应点对;
(5)利用剩余的正确对应关系来估算刚体变化,求解对应旋转矩阵和平移矩阵,完成配准构成。
二、点云配准分类
国内外许多学者都对其进行了深入的研究,也取得了丰硕的研究成果。应用较为广泛是迭代最近点、基于几何特征匹配、基于图像灰度的配准等。这些配准算法所用到的几何原理主要包括刚性变换、投影变换、放射变换和曲线变换。虽然每种配准算法的原理不同,但配准的流程都相差不大,主要分为:点云数据的提取、点云数据的匹配、除错处理和变换求解。
1. 无辅助的自动拼接
针对特征明显的被测物体,使用其他手段进行配准、
(1)迭代最近点(ICP):从一片点云中搜索到另外一片点云中最近点来确定对应点集,容易陷入局部最优解,且要求配准两片点云初始位置与真实位置相差不大,其实质是基于最小二乘法的最优匹配方法。主要分为点对点,点对投影和点对面的方法。
(2)特征点匹配:通过分析被测物体的局部几何信息来寻找特征点并实现匹配,但算法特征点包含较少几何信息,稳定性有待提高。可以利用多尺空间尺度不变特征变化(SIFT)来寻找特征点,这要求被测物体有纹理信息,基于SIFT算法在空间寻找极值点,并提取其位置、尺度、旋转不变量进行特征点匹配。
(3)正态分布变换(NDT):利用高斯概率分布的形式来描述离散点的信息,用标准最优化技术确定最优匹配,具有收敛速度快,效率高的特点,常常用来做精配准,结合其他算法一起使用。
(4)依靠平台实现配准:通过扫描设备和旋转平台之间的相对位置,通过旋转平台运动参数来计算各个点云视角下旋转矩阵,实现将任意角度的点云配准到统一坐标系下,该方法配准精度高,但受旋转平台定位装置精度的影响。
2. 人工辅助标志点
针对被测物体没有明显的特征点,从不同的视角拍摄无法对同一点进行有效的识别定位,需要人工添加标志点在被测物体上,进而完成测量。这种方式更加灵活、适用于任何形状的物体。
(1)编码标志点:标志点自身带有唯一的编码信息,每个标志点都对应不同的编码信息,且对于不同的编码标志点有对应不同的编解码方案和特征识别算法,通过在两幅不同视场下相同的标志点实现自动拼接。
(2)非编码标志点:标志点的大小形状完全相同,可以通过对三点法、四点法、四元法、SVD最小二乘法实现点云配准。但由于噪声的影响标志点位置布置的随机性,在标志点匹配时非常同意出现误匹配标志点,影响点云配准的稳定性。
三、配准常见流程
通过一个点集(目标)中的每一个点与另一个点集(原始点集)中的对应点的相互关系来实现点集与点集坐标系之间的转换,实现配准。
两幅点云数据中对应点的坐标关系可以描述如下: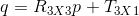
其中其中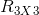 (R)是对应点旋转矩阵,
(R)是对应点旋转矩阵,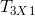 (T)是对应点平移矩阵。
(T)是对应点平移矩阵。
估算变换矩阵的步骤:
(1) 在对应关系的基础上评估一些错误的度量标准(使用对应点的欧式距离为度量标准);
(2)利用最小化错误标准和矩阵运算等来估计一个刚性变换;
(3)使用刚性变换将源点云旋转/平移到与目标所在的同一个坐标系下,然后再用所有对应点或者部分对应点、关键点运行一个内部ICP循环;
(4)进行迭代,直到符合收敛性判断标准为止(一般设置对应点的欧氏距离作为终止迭代的阈值)
求解旋转矩阵可以通过在两个点云集中寻找对应点对,根据对应点对来建立转换方程组,通过求解方程组的值来计算出旋转矩阵R和平移矩阵 H。理论上最少需要找到三组不共线的对应点对才能求解出旋转平移矩阵,不过为使结果更加精确,对应点对越多越好。但一般情况下,很难在两幅点云数据中很准确的找到对应点对,因此加入目标函数,使目标函数最优来估计旋转、平移矩阵。目前,最常用的目标函数是对应点欧式距离平方和:
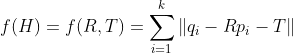
大部分点云配准算法可以从不同角度对其进行划分:从局部与整体的角度进行划分时,可以分为局部配准与全局配准;从配准精确度高低的角度进行划分时,可以分为粗配准与精确配准。虽然划分的方式不同,但不同角度之间是相互对应的,全局配准与粗配准对应,局部配准与精确配准对应。、
大多是点云数据的配准主要基于迭代最近点算法。由于迭代最近点算法对待配准的两片初始点云有较高的重叠度要求,因此在精确配准之前要进行粗配准。通过粗配准可以得到矩阵变换参数,进而将待配准点云数据转换到统一坐标系内,为精确配准提供一个较好的初始位置。
1. 粗配准
粗配准是为了后续ICP精配准做准备,初步对两片初始点云进行配准,可到平移矩阵和旋转矩阵的初始值,进而将待配准点云数据转换到统一坐标系内,为精确配准提供一个较好的初始位置。根据被测物体本身所具有的特点不同,较为常见的粗配准方法有:标签法、基于平台配准和曲率特征法。
(1)标志点:通过人为的在被测物体表面贴标签,将这些标签作为被测物体的特征点,在对多次测量得到的点云数据进行配准时,通过对特征点的进行识别与配准,代替了对整体点云数据的配准,简化了点云数据的配准过程。
标志点缺点是对测物体进行贴标签的操作比较繁琐,过程比较耗时,并且对文物类的实体进行测量时,有可能产生不同
程度的损坏。
(2)基于平台配准:将被测物体放在平台之上,利用控制器对平台进行控制,使得平台进行固定角度的转动,通过对同一位置的多次测量便可得到不同视角下的点云数据,进而实现对被测物体的点云配准。
基于平台配准主要适用于那些尺寸比较小且不适合贴标签的物体。
(3)曲率特征法:通常用于被测物体的表面几何特征较为明显的情况,因为曲率是空间几何里的一个不变特征量,所以通过曲率值的计算可以确定两片点云的对应点对,进而利用得到的对应点对求解变换矩阵的未知参数,完成点云的粗配准。
2. 精配准
ICP由于具有计算简便直观,配准精度高等优点被广泛应用于点云的精配准中。但该算法的运行速度以及向全局最优化的收敛性却在很大程度上依赖于给定的初始变换估计以及在迭代过程中对应关系的确立。所以需要各种粗配准技术为ICP算法提供较好的位置,在迭代过程中确立正确对应点集能避免迭代陷入局部极值,决定了算法的收敛速度和最终的配准精度。
ICP处理流程:(1)对原始点云数据进行采集;(2)确定初始对应点集;(3)去除错误点对应点对;(4)变换矩阵的求解。
首先是从源点云中搜索到目标点云中最近点来确定对应点集q和p,然后通过最小二乘法迭代求解最优旋转矩阵R和平移矩阵T,使得误差E最小:
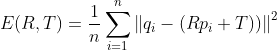
其中n代表对应点对的数目,ICP算法具有计算简单且配准精度高的优点,但是该算法对于两片点云的初始位置要求较为严格,否则容易陷入局部收敛且会影响配准速度,因此需要通过粗配准来为ICP提供较好的点云初始位置。
常用求取目标函数最小的旋转矩阵和平移矩阵的方法主要分为四元数法和奇异值分解法。
(1)奇异值分解求解
由最小二乘法可知目标函数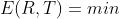
求两组点云集的重心:
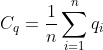
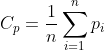
由最小二乘法可知: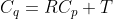 ,并定义
,并定义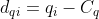 ,
,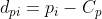 ,于是目标函数可以变为:
,于是目标函数可以变为:
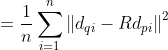
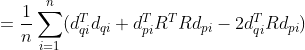
因为第一项与R无关,第二项由于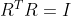 与R无关(R为正交矩阵),那么目标函数可以转化为求
与R无关(R为正交矩阵),那么目标函数可以转化为求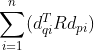 的最大值。
的最大值。
令
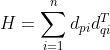
假设存在最优解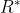 ,则存在下面关系:
,则存在下面关系:
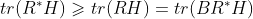
则然后对H矩阵进行奇异值分解(SVD)
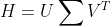
于是可以得到最优解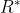
其中需要H满秩,同时需要det(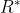 )=1。然后通过
)=1。然后通过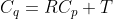 可以求得平移矩阵T。
可以求得平移矩阵T。
(2)四元素求解旋转矩阵
前提背景:三维空间的任意旋转,都可以用绕三维空间的某个轴旋转过某个角度来表示,即所谓的Axis-Angle表示方法。于是我们可以用一个四维向量就可以表示出三维空间任意的旋转。这里的三维向量
只是用来表示Axis的方向朝向,因此更紧凑的表示方式是用一个单位向量来表示方向Axis,而用该三维向量的长度来表示角度值θ。于是就可以用一个三维向量
就可以表示出三维空间任意的旋转。
单位向量旋转θ角度后的四元数:
对于三维坐标的旋转,可以通过四元数乘法直接操作,与旋转矩阵操作可以等价,但是表示方式更加紧凑,计算量也可以小一些。
根据上面的背景,我们可以定义一个单位四元数来表示旋转:
其中均为实数,
对于本身的几何意义可以理解为一种旋转,其中
代表 x 轴与 y轴相交平面中 xx轴正向向 y 轴正向的旋转,
旋转代表 z 轴与 x 轴相交平面中 z轴正向向 x轴正向的旋转,
旋转代表 y 轴与 z 轴相交平面中 y 轴正向向 z 轴正向的旋转,
分别代表
的反向旋转。
四元数性质:
单位四元数的共轭和逆相等:
四元数的乘法:,
由上式可以得知四元数不具备有乘法交换律性质。
根据上面介绍背景和四元数的性质,假设三维空间点云中某个数据点的四元数的形式:
设过原点的旋转轴的单位方向向量为,某点P绕旋转轴旋转
角度后得到了
,此旋转过程的四元数表示形式为:
由于采用单位四元数的表达形式,所以,而且
。
因此点与点
满足以下关系:
联立上面四元数的乘法两条公式可以得到如下关系:
为了消除符号歧义,中符号
均用
。通过对比旋转矩阵
的形式,可以得出用四元数形式表示的旋转矩阵:
利用四元数作为旋转向量的表示优势:不需要考虑多个轴的旋转顺序且复杂计算,只用绕一个轴旋转角度来表示整体的旋转,计算较为简单;且能避免由于建立在物体坐标系上导致万向节死锁。唯一缺点是多引入一个变量,但这并不影响旋转矩阵的确定。
根据上文推导,对于两片点云之间的高精度配准是通过最小二乘法迭代求解最优旋转矩阵R和平移矩阵T,使得误差E最小:
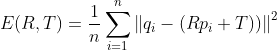
求两组点云集的重心:
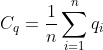
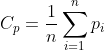
然后对两片点云做去中心化处理后,求出两片点云的协方差矩阵:
并假设对称矩阵:
由此可以得到列向量为:
利用该列向量构建4X4对称矩阵:
其中,表示矩阵
的迹,即主对角线元素的综合,也是特征值之和,
表示
的单位矩阵。所以将上面矩阵B进一步计算可以得到如下方程:
然后对矩阵B做特征值和特征向量求解,求出最大的特征值以及其对应的特征向量,那个特征向量就对应误差的平方和最小时的四元数。(这个我也不是很清楚,为什么这个特征向量就对应误差平方和最小时的四元数???)
求出四元数的四个变量值:。并且将其四个值带入到上式的旋转矩阵R中,求解最优的旋转矩阵。在选择矩阵确定后,根据公式
,就容易求解出平移矩阵。计算目标函数如下式,如果结果小于阈值则停止迭代,否则继续重复前面的步骤。
参考文献
1.SVD求解ICP:https://blog.csdn.net/zhouyelihua/article/details/77807541
2.四元数性质:https://blog.csdn.net/lql0716/article/details/72597719
3.四元数求解ICP:https://blog.csdn.net/hongbin_xu/article/details/80537100























 2207
2207

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








