从二维坐标系说起:
二维平面直角坐标系定义可分为两类,从逆时针角度看,第一类为X坐标轴在Y坐标轴后;第二类为X坐标轴在Y坐标轴前。
有这两类坐标系添加第三个坐标轴Z,得到空间直角坐标系,在默认添加的坐标轴Z垂直纸面朝向外侧下,分别得到左手空间直角坐标系和右手空间直角坐标系。
而对于坐标的转换,最简单的依然从二维坐标系讲起。
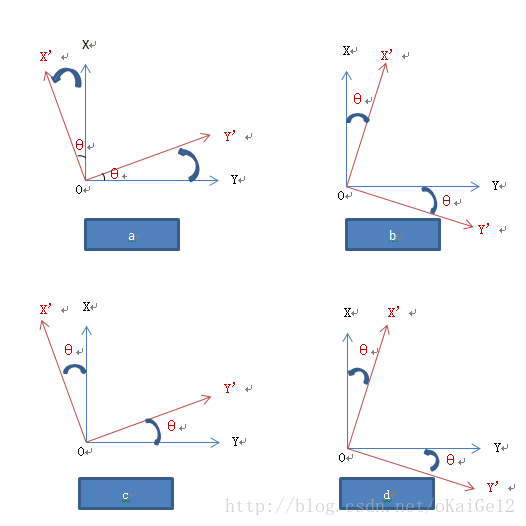
以第一类二维平面直角坐标为例,涉及的坐标转换有下图中4种情况:a,b,c,d.
基础一 原坐标系坐标转到新坐标系
a与b为已知原坐标系下坐标,从原坐标系(蓝色表示)旋转角度θ,获得新坐标系下坐标(红色表示):
此处注意:定义角度的正负应统一,即存在原坐标系与新坐标系的概念,新坐标系相对于原坐标系的旋转角度为逆时针时为正值。
针对情况a有:
即:
(注:从简单直观方面理解为,当原坐标系转角度θ到新坐标系过程中,y坐标值在新坐标系中是变大的,x坐标值在新坐标系中是变小的。因此,y方向的三角系数都为正,x方向存在负值情况。可以标记为沿旋转方向数,第一条坐标轴数值是变大的,条件是旋转方向角度为无符号数值。)
因此,针对a和b两种情况,由原坐标系经过旋转一定角度,转换到新的坐标系下,得到的旋转矩阵为:
其中θ为具有正负号的角度值,当为正值时代表原坐标系沿逆时针旋转;为负值时代表原坐标系沿顺时针旋转。
基础二 新坐标系坐标转回原坐标系
而情况c与d是表示已知新坐标系下坐标,经过坐标转换获得在原坐标系下坐标:
此处注意:定义角度的正负应统一,即存在原坐标系与新坐标系的概念,新坐标系与原坐标系的旋转角度为逆时针时为正值。
在c与d情况中,因为定义了逆时针旋转角度为正,所以c中旋转的角度为(-θ),d中旋转的角度为(θ)。而沿逆时针旋转时,在该方向上第一条坐标轴为Y轴,所以基本公式为:
小结:
定义了坐标轴的指向,以及新坐标系与原坐标系旋转角度的正负关系后,可以确定原坐标系转到新坐标系运算与你运算正弦系数符号变换。
因此,要确定旋转矩阵内容必须要确定两个因素,一是坐标轴的指向,二是旋转角度的正负定义。
(1)当存在原坐标系与新坐标系概念时,必然的旋转角度的正负定义必须一致,此时由原坐标系到新坐标系的转换,可严密的进行返回坐标转换。
(2)当只存在当前坐标系下坐标转到另一个坐标系下坐标时,根据确定的旋转角度正负,参考基础一即可转换。基础一中只表示了逆时针旋转角度为正的情况,顺时针旋转为正的情况可仿照进行。
(3)无论什么情况下,选取旋转角度定义为正(无论逆时针还是顺时针旋转)时作为基础,沿旋转方向数的第一条坐标轴的坐标值应变大,即在新坐标系下对应该坐标轴上的坐标值组合为cos+sin的形式,而另一坐标轴上坐标值为-sin+cos形式。
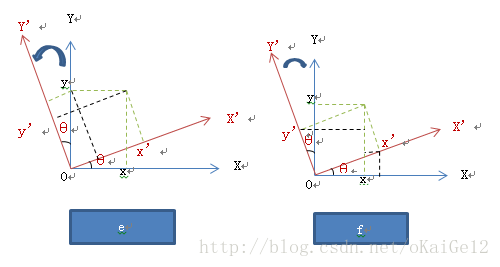
在基础一与基础二中都可印证(3)的说明。再增加一条印证示例:
在情况e中,定义从蓝色坐标系旋转到红色坐标系,定义图中状态的旋转角度θ为正,则此时坐标转换关系为:
情况f中,依然定义图中状态为旋转角度θ为正值,但是从红色坐标系转到蓝色坐标系:
从旋转方向遇到的第一个坐标轴Y坐标开始整理,则有:
旋转矩阵的形式依然是正规形式,以x,y为顺序排列为:
在情况e中定义了目标坐标系在原坐标系的逆时针方向为正,情况f中定义了目标坐标系在原坐标系的顺时针方向为正,这两种情况从纯坐标系的转换方面印证了上面(3)中总结的,即以正值旋转角度为基础,沿旋转方向第一条坐标轴上的坐标为cos+sin形式:e中第一条坐标轴为x轴,f中第一条坐标轴为y轴。从坐标转换与逆转换方面印证了(1)中总结结果,即存在正转换与逆转换时,定义的正旋转角度应一致,此时的正反旋转矩阵相乘为单位矩阵。
基础三 平面坐标系中讨论左右手系的转换问题
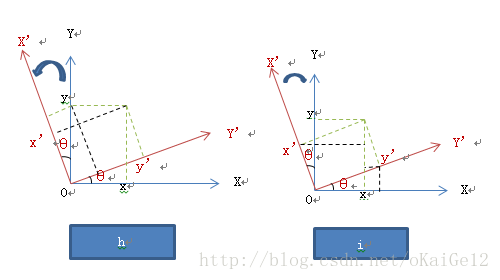
情况h中从蓝色坐标系旋转角度θ到红色坐标系下,两坐标系的坐标轴向定义不同,产生类似左右手系问题,在这类转换中,首先将目标坐标系的轴向假设与原坐标系轴向定义为一类,然后更换坐标符号获得两坐标系的转换。
第一步:假设X’与Y’轴互换,此时原坐标系与目标坐标系定义类似,相差角度θ,定义目标坐标系与原坐标系之间逆时针旋转角度为正,得到:
根据假设坐标与真实坐标关系获得两坐标系真实关系:
按顺序排放整理:
即,进行左右系的坐标系转换时的旋转矩阵为:
以情况i作为验证示例:
依然定义目标(红)坐标系转到原(蓝)坐标系时,目标坐标系相对原坐标系旋转角度为逆时针时为正。
假设原坐标系的坐标轴向与目标坐标系的轴向类似定义,为x(伪),y(伪)。
则
按顺序整理得到:
得由目标坐标系转回原坐标系的旋转矩阵为:
由
得该转换过程成立。
小结:在处理坐标系向量的顺序整理时需要进行公式的元素调换。
(1) 针对等号左边结果的调换如
要变为
时,只需等号右面矩阵的行进行相应对调:
(2) 只针对等号右面最后原坐标值向量内容调换时,等式的左右都需要变化。如
但是要保持等号左边的向量顺序不变时需要两步:
第一步:首先利用(1)将等号左边向量调换为:
验证,变换后的结果与初始状态一致。
基础四 三维空间直角坐标系的正转换问题
三维空间直角坐标的坐标转换可由二维平面直角坐标转换扩展来,在二维坐标系中的坐标转换只有一个角度的旋转,也就产生一个旋转矩阵。在三维空间直角坐标系中存在三个方向的角度旋转问题,因此产生三个旋转矩阵相乘的结果。但是针对沿某一坐标轴旋转某一角度时,又回归到二维坐标旋转问题。因此,三维空间直角坐标的坐标旋转问题是三个二维平面直角坐标旋转问题的顺序操作问题。(但是由于某一角度旋转后,后一角度的旋转是否对前者有耦合效应,应该深入研究探讨)
下面首先讨论三维空间直角坐标系的坐标转换问题。
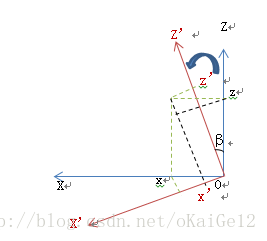
以右手坐标系为例,研究原坐标系到新坐标系经过首摇,纵摇,横摇角度的转换过程以及逆过程。
A 原坐标系转换到新坐标系
首先定义坐标系以及旋转角度的正负定义
定义右手坐标系如图,沿各坐标轴正向的反方向看,另外两坐标平面沿逆时针旋转时,定义为沿该坐标轴正角度旋转。
由此定义沿X,Y,Z轴逆时针旋转角分别为α,β,γ。
从X->Y->Z轴的顺序,分别分析坐标转换矩阵的形式。
沿X轴方向旋转α角度时对应的关系图
根据图中关系可以得到第一次转换后的坐标,由于沿X轴旋转,所以新坐标中X信息不变。根据以上基础问题的讨论可以得到:
沿Y轴方向旋转β角度时对应的关系图
根据图中关系可以得到第二次转换后的坐标,由于沿Y轴旋转,所以新坐标中Y信息不变。根据以上基础问题的讨论可以得到:
注:沿Y的旋转矩阵与沿X轴的旋转矩阵形式出现不同,原因在于,当沿X轴旋转时,沿正旋转角度的第一条边为Y轴,即Y值变大。而沿Y轴进行旋转时,第一条边Z轴的对应值变大,而在向量摆放时Z值放在最下方,因此利用基础问题三中的等号右边最后向量重现摆放时需要整体变换,变换结果为以上所示。
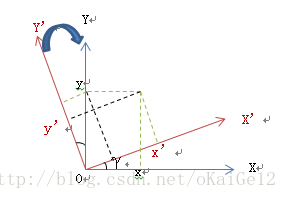
沿Z轴方向旋转γ角度时对应的关系图
根据图中关系可以得到第三次转换后的坐标,由于沿Z轴旋转,所以新坐标中Z信息不变。根据以上基础问题的讨论可以得到:
注:沿Z轴与沿X轴的旋转矩阵类似,因为这两种情况下按旋转方向得到的坐标轴顺序与XYZ顺序一致,因此不需要进行顺序重排,而沿Y轴旋转时,Z轴在X轴前面,因此需要重排顺序,重排后,矩阵形式发生变化。从另一个角度说,当沿Z轴和X轴旋转时,坐标变大的分别为X值和Y值,因此其对应的矩阵行都为正,沿Y轴旋转时,坐标变大的为Z值,因此Z坐标对应的行矩阵系数为正。
如果知道原坐标系通过沿X、Y、Z轴的顺序进行旋转到新坐标系,则新坐标系下坐标为:
基础五 三维空间直角坐标系的逆转换问题
若已知从原坐标系到新坐标系的角度旋转关系,如原坐标系首先沿X轴旋转α,然后沿Y轴旋转β,最后沿Z轴旋转γ。则坐标正转换时(即)的公式:
进行三维坐标逆转换时,一致新坐标系下坐标,以及新旧坐标系的角度旋转顺序和信息。
则由以上信息可推测坐标逆转换为:
R(α)与R’(α),R(β)与R’(β),R(γ)与R’(γ)互为逆矩阵。旋转顺序为沿Z轴、Y轴和X轴进行转换。
1.首先从Z轴转换:
定义的沿Z轴逆时针旋转时角度为正,此时进行的坐标转换为从红色坐标系到原坐标系的旋转,即旋转角度为(-γ)。针对从新坐标系(0-X’Y’Z’)到原坐标系的逆转换有两种方式:
(1) 采用原坐标系到新坐标系的旋转角度正负定义获取坐标转换公式,然后将(-γ)代入公式即可:
根据前面所讲,确定旋转矩阵时,根据旋转角θ正方向和第一个坐标轴X’可快速确定旋转公式:
将实际旋转角度(-γ)代入得:
(2) 不考虑整个系统定义的角度正负(此时适应条件中只给出两坐标系间的相差的角度,没有正负定义时),按给出的角度(数值应为一个正值)和两坐标系的实际旋转关系确定旋转矩阵。此时,由新坐标系(0-X’Y’Z’)顺时针方向旋转角度γ得到原坐标系下坐标,则在沿旋转方向中第一条坐标轴为Y轴(即数值变大轴):
方法(1)和方法(2)的结果完全相同。但是方法(1)存在角度的正负定义问题,并且前后连贯一致,多在测绘中的姿态仪中出现,对于姿态仪中给出的姿态角度可以用一套公式表示(如方法1中结果的第一种表达方法),而方法(2)只存在一种结果形式,因此不适用存在整体性角度正负定义的问题。
则沿Z轴的旋转矩阵
2.沿Y轴转换
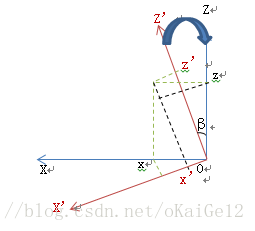
沿Y轴方向旋转角度时对应的关系图
根据图中关系可以得到沿Y轴顺时针旋转β角度到原坐标系下,从定义的沿Y轴逆时针方向旋转角度为正的角度确定旋转角度为(-β)。在该图中沿正旋转角度时,第一个坐标轴为Z轴,所以得到的基本旋转矩阵为:
3.沿X轴旋转
沿X轴方向旋转α角度时对应的关系图
由于沿X轴旋转,所以新坐标中X信息不变。沿X轴顺时针旋转角度α得到原坐标系下坐标。根据定义的角度旋转正负关系,定义逆时针旋转角度为正,因此旋转的角度为(-α)。沿X轴逆时针正旋转时,第一个坐标轴为Y轴,因此基本公式为:
综上,经过沿Z-Y-X轴的坐标你旋转,将在新坐标系下坐标转回到原坐标系下:
总结:从一个坐标系转到新坐标系,一般需要定义旋转角度的正负,一旦正负的方向定义后,从原坐标系到新坐标系的旋转和从新坐标系到原坐标系的旋转都可用这一个方向定义,此时需要考虑的是操作中出现了从原坐标系到新坐标的正转换和新坐标系到原坐标系的逆转换,逆转换时须将采集的原坐标系到新坐标系的旋转角度取反代入同一套公式。
另一种方法,对于只使用从原坐标系到新坐标系或者只使用新坐标系到原坐标系的旋转过程时,可以单独对旋转过程定义一套旋转角度正负使用问题,比如姿态中的横摇一般定义为右舷下降为正值,那么假设当前横摇值为+10°,要从姿态传感器坐标系到水平坐标系,在XOZ平面,认为顺时针方向旋转为正值,则此时X轴坐标值应为旋转变大方,因此系数组合为Xcos+Zsin模式,旋转矩阵也就确定下来了。该例子中,旋转矩阵的确定存在一下2个条件:(1)直接使用了姿态仪给出的数值;(2)定义了顺时针方向为正方向(只有这样定义,才能直接用姿态仪给出的数值,否则要取反使用).










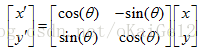




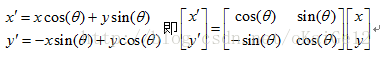

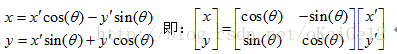

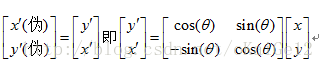
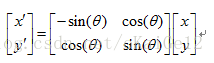

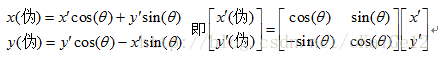
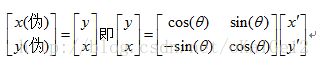
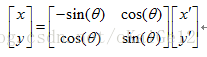
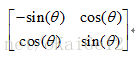

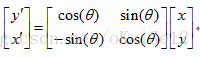
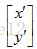
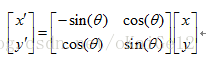

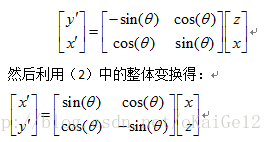






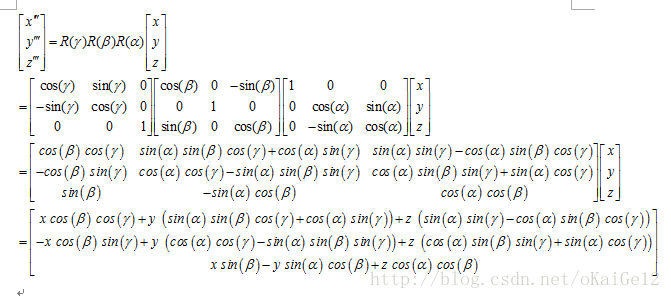




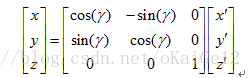

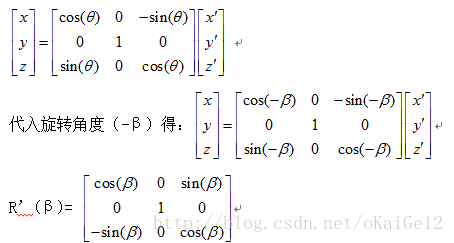

















 5711
5711











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








