文章目录
本课程来自深度之眼deepshare.net,部分截图来自课程视频。
内容概要
学习权值初始化的原理;介绍损失函数、代价函数与目标函数的关系,并学习交叉熵损失函数
权值初始化
之前的课程学习了模型的构建,这次课学习权值的初始化,正确的初始化权值可以加快模型的收敛,是炼丹技能中必备的属性点。
梯度消失与爆炸

在前向传播过程中求
W
2
W_2
W2的梯度为下面的式子:
Δ
W
2
=
∂
L
o
s
s
∂
W
2
=
∂
L
o
s
s
∂
o
u
t
∗
∂
o
u
∂
H
2
∗
∂
H
2
∂
W
2
\Delta W_2=\frac{\partial Loss}{\partial W_2}=\frac{\partial Loss}{\partial out}*\frac{\partial ou}{\partial H_2}*\frac{\partial H_2}{\partial W_2}
ΔW2=∂W2∂Loss=∂out∂Loss∗∂H2∂ou∗∂W2∂H2
观察最后一项,由式子
H
2
=
H
1
∗
W
2
H_2=H_1*W_2
H2=H1∗W2可知,上式等于:
=
∂
L
o
s
s
∂
o
u
t
∗
∂
o
u
∂
H
2
∗
H
1
=\frac{\partial Loss}{\partial out}*\frac{\partial ou}{\partial H_2}*H_1
=∂out∂Loss∗∂H2∂ou∗H1
得到梯度消失和爆炸的原因:
梯度消失:
H
1
→
0
→
Δ
W
2
→
0
H_1→0→\Delta W_2→0
H1→0→ΔW2→0
梯度爆炸:
H
1
→
∞
>
Δ
W
2
→
∞
H_1→\infty>\Delta W_2→\infty
H1→∞>ΔW2→∞
也就是说要避免梯度消失和爆炸就是要控制网络网络中间输出值的范围,不能太大也不能太小。
下面通过一些推导来看看为什么会出现梯度消失和爆炸。
公式1中E代表期望,公式2中D代表方差。X和Y是两个独立的随机变量。
1.
E
(
X
∗
Y
)
=
E
(
X
)
∗
E
(
Y
)
E(X*Y)=E(X)*E(Y)
E(X∗Y)=E(X)∗E(Y)
2.
D
(
X
)
=
E
(
X
2
)
−
[
E
(
X
)
]
2
D(X)=E(X^2)-[E(X)]^2
D(X)=E(X2)−[E(X)]2
3
.
D
(
X
+
Y
)
=
D
(
X
)
+
D
(
Y
)
.D(X+Y)=D(X)+D(Y)
.D(X+Y)=D(X)+D(Y)
通过上面三个式子可以推出:
D
(
X
∗
Y
)
=
D
(
X
)
∗
D
(
Y
)
+
D
(
X
)
∗
[
E
(
Y
)
]
2
+
D
(
Y
)
∗
[
E
(
X
)
]
2
D(X*Y)=D(X)*D(Y)+D(X)*[E(Y)]^2+D(Y)*[E(X)]^2
D(X∗Y)=D(X)∗D(Y)+D(X)∗[E(Y)]2+D(Y)∗[E(X)]2
通常的,若X和Y满足各自的期望为0,即:
E
(
X
)
=
0
,
E
(
Y
)
=
0
E(X)=0,E(Y)=0
E(X)=0,E(Y)=0,则上式简化变为:
D
(
X
∗
Y
)
=
D
(
X
)
∗
D
(
Y
)
D(X*Y)=D(X)*D(Y)
D(X∗Y)=D(X)∗D(Y)
下面来看看网络层中某个神经元的标准差是怎么样的,例如下图中
H
11
H_{11}
H11的计算:

H
11
=
∑
i
=
0
n
X
i
∗
W
1
i
H_{11}=\sum_{i=0}^nX_i*W_{1i}
H11=i=0∑nXi∗W1i
H
11
H_{11}
H11的方差为:
D
(
H
11
)
=
∑
i
=
0
n
D
(
X
i
)
∗
D
(
W
1
i
)
(1)
D(H_{11})=\sum_{i=0}^nD(X_i)*D(W_{1i}) \tag{1}
D(H11)=i=0∑nD(Xi)∗D(W1i)(1)
由于
X
i
X_i
Xi和
W
1
i
W_{1i}
W1i都服从正态分布,因此他们两个的方差都为1。
=
n
∗
(
1
∗
1
)
=n*(1*1)
=n∗(1∗1)
=
n
=n
=n
H
11
H_{11}
H11的标准差为:
s
t
d
(
H
11
)
=
D
(
H
11
)
=
n
std(H_{11})=\sqrt{D(H_{11})}=\sqrt{n}
std(H11)=D(H11)=n
由上面的计算可以知道,当输入经过一层传播后,他的方差变大了n倍,标准差变大了
n
\sqrt{n}
n倍,如果从
H
11
H_{11}
H11往下传播到
H
21
H_{21}
H21,则同样的,方差会变大n倍,标准差变大
n
\sqrt{n}
n倍。经过很多层的传播后,方差和标准差不断变大,最后超出可计算的范围,变成NAN,梯度就爆炸了。。。。
例如:一个FC的每个隐藏层神经元个数是400,输入X服从正太分布,用PyTorch进行计算每一层的std:

400个神经元开根号就是20,每层增加大约20倍。
从上面公式(1)中的计算我们知道,网络隐藏层的输出值的方差和三个东西有关系,一个是n,一个是输入值的方差
D
(
X
i
)
D(X_i)
D(Xi),一个是权值的方差
D
(
W
1
i
)
D(W_{1i})
D(W1i)。也就是说要想让方差保持某一个范围尺度,不能太大和太小,就需要方差的值为1,即:
D
(
H
11
)
=
n
∗
D
(
X
)
∗
D
(
W
)
=
1
D(H_{11})=n*D(X)*D(W)=1
D(H11)=n∗D(X)∗D(W)=1
这里面n和输入X都是我们不能设置的,唯一能让炼丹师调整的就是超参数W了,如果我们将W的设置,使其满足如下条件,就能让方差为1:
D
(
W
)
=
1
n
即
:
s
t
d
(
W
)
=
1
n
D(W)=\frac{1}{n}即:std(W)=\sqrt{\frac{1}{n}}
D(W)=n1即:std(W)=n1
但是以上模型的网络结构中没有考虑激活函数,如果加入激活函数,例如:tanh,会发现标准差会变得越来越小,就是梯度会慢慢消失的。
这就没法玩了,于是又炼丹高人想了一个办法来解决这个问题:
xavier方法与Kaiming方法
xavier方法
参考文献:《Understanding the difficulty of training deep feedforward neural networks》
方差一致性:保持数据尺度维持在恰当范围,通常方差为1
适用激活函数:饱和函数,如Sigmoid,Tanh
参考文献中,给出了下面两个等式:
n
i
∗
D
(
W
)
=
1
n_i*D(W)=1
ni∗D(W)=1
n
i
+
1
∗
D
(
W
)
=
1
n_{i+1}*D(W)=1
ni+1∗D(W)=1
其中
n
i
n_i
ni是输入层神经元的个数,
n
i
+
1
n_{i+1}
ni+1是输出层神经元的个数。上面考虑了前向和反向传播,就是翻来覆去梯度都不能出现爆炸和消失,要满足上面两个条件,就得到如下式子:
D
(
W
)
=
2
n
i
+
n
i
+
1
(2)
D(W)=\frac{2}{n_i+n_{i+1}}\tag{2}
D(W)=ni+ni+12(2)
这还没有完,接下来可以根据这个思想来推导均匀分布上下限为[-a,a] (我们的输入是0均值,所以上下限是对称的。)的时候W的方差取值是什么:
W
∼
U
[
−
a
,
a
]
W\sim U[-a,a]
W∼U[−a,a]
D
(
W
)
=
(
−
a
−
a
)
2
12
=
(
2
a
)
2
12
=
a
2
3
(3)
D(W)=\frac{(-a-a)^2}{12}=\frac{(2a)^2}{12}=\frac{a^2}{3}\tag{3}
D(W)=12(−a−a)2=12(2a)2=3a2(3)
这里涉及到均匀分布的方差计算,可以点我看推导。
然后要让公式(2)和(3)要相等:
2
n
i
+
n
i
+
1
=
a
2
3
\frac{2}{n_i+n_{i+1}}=\frac{a^2}{3}
ni+ni+12=3a2
a
=
6
n
i
+
n
i
+
1
a=\frac{\sqrt{6}}{\sqrt{n_i+n_{i+1}}}
a=ni+ni+16
W
∼
U
[
−
6
n
i
+
n
i
+
1
,
6
n
i
+
n
i
+
1
]
W\sim U[-\frac{\sqrt{6}}{\sqrt{n_i+n_{i+1}}},\frac{\sqrt{6}}{\sqrt{n_i+n_{i+1}}}]
W∼U[−ni+ni+16,ni+ni+16]
手工计算:
a=np.sqrt(6/(self.neural_num+self.neural_num))
自动计算:
nn.init.xavier_uniform_(m.weight.data,gain=tanh_gain)
xavier方法只适用用饱和激活函数,后来出现的ReLU激活函数就不行了(会爆炸),于是另外一个大佬何凯明提出另外一种初始化方法:
Kaiming方法
参考文献:《Delving deep into rectifiers:Surpassing human-level performance on ImageNet classification》
方差一致性:保持数据尺度维持在恰当范围,通常方差为1
适用激活函数:ReLU及其变种。
参考文献中,给出了下面两个等式:
D
(
W
)
=
2
n
i
D(W)=\frac{2}{n_i}
D(W)=ni2
D
(
W
)
=
2
(
1
+
a
2
)
n
i
D(W)=\frac{2}{(1+a^2)n_i}
D(W)=(1+a2)ni2
a是ReLU函数在负半轴的斜率,普通ReLU函数斜率为0,变种的化就带入具体值。最后给出标准差的公式:
s
t
d
(
W
)
=
2
(
1
+
a
2
)
n
i
std(W)=\sqrt{\frac{2}{(1+a^2)n_i}}
std(W)=(1+a2)ni2
nn.init.kaiming_normal_(m.weight.data)
常用初始化方法(十种四大类)
第一类:Xavier
1.Xavier均匀分布
2.Xavier标准正态分布
第二类:Kaiming
3.Kaiming均匀分布
4.Kaiming标准正态分布
第三类:常用分布
5.均匀分布
6.正态分布
7.常数分布
第四类:特殊矩阵
8.正交矩阵初始化
9.单位矩阵初始化
10.稀疏矩阵初始化
参考:https://pytorch.org/docs/stable/nn.init.html
特殊函数:
nn.init.calculate_gain
主要功能:计算激活函数的方差变化尺度主要参数(就是输入的方差与输出的方差的比例,用于观察方差的变化,例如tanh的calculate_gain结果大约是1.6左右,就可以知道,经过tanh输出的方差会比输入的方差减小1.6倍)
·nonlinearity:激活函数名称
·param:激活函数的参数,如Leaky ReLU的negative_slop
损失函数
损失函数概念
损失函数是什么
损失函数:衡量模型输出与真实标签的差异
下图中,绿色点是训练样本,蓝色线是训练好的模型,这里的红色线就是差异,衡量差异这里用的是:
∣
y
^
−
y
∣
|\widehat y-y|
∣y
−y∣

损失函数(Loss Function):
L
o
s
s
=
f
(
y
^
,
y
)
Loss=f(\widehat y,y)
Loss=f(y
,y),损失函数是计算一个样本的差异。
代价函数(Cost Function):
C
o
s
t
=
1
N
∑
i
N
f
(
y
^
,
y
)
Cost=\frac{1}{N}\sum_i^Nf(\widehat y,y)
Cost=N1∑iNf(y
,y),代价函数是计算整个样本损失函数的平均值(求和再平均)。
目标函数(Objective Function):
O
b
j
=
C
o
s
t
+
R
e
g
u
l
a
r
i
z
a
t
i
o
n
Obj=Cost+Regularization
Obj=Cost+Regularization,目标函数除了要使得代价函数尽可能的小之外,还要考虑一些约束,防止过拟合。
PyTorch的损失函数
红线去掉的两个参数将在新版本中去掉。Loss基类继承自Module

1、nn.CrossEntropyLoss
功能:nn.LogSoftmax()与nn.NLLLoss()结合,进行交叉熵计算,这里的target中的变量类型是long
主要参数:
·weight:各类别的loss设置权值,设置权值后求均值是按加权求均值
·ignore_index:忽略某个类别
·reduction:计算模式,可为none/sum/mean
none-逐个元素计算
sum-所有元素求和,返回标量
mean-加权平均,返回标量
接下来是一些补充内容:
交叉熵=信息熵+相对熵
交叉熵:
H
(
P
,
Q
)
=
−
∑
i
=
1
N
P
(
x
i
)
l
o
g
Q
(
x
i
)
H(P,Q)=-\sum_{i=1}^NP(x_i)logQ(x_i)
H(P,Q)=−∑i=1NP(xi)logQ(xi)
自信息:
l
(
x
)
=
−
l
o
g
[
p
(
x
)
]
l(x)=-log[p(x)]
l(x)=−log[p(x)],对概率取对数
熵也叫信息熵,是一个概率分布:
H
(
P
)
=
E
x
∼
p
[
I
(
x
)
]
=
−
∑
i
=
1
N
P
(
x
i
)
l
o
g
P
(
x
i
)
H(P)=E_{x\sim p}[I(x)]=-\sum_{i=1}^NP(x_i)logP(x_i)
H(P)=Ex∼p[I(x)]=−∑i=1NP(xi)logP(xi)
相对熵,两个熵的分布间差异:
D
K
L
(
P
,
Q
)
=
E
x
∼
p
[
l
o
g
P
(
x
)
Q
(
x
)
]
D_{KL}(P,Q)=E_{x\sim p}[log\frac{P(x)}{Q(x)}]
DKL(P,Q)=Ex∼p[logQ(x)P(x)]
=
E
x
∼
p
[
l
o
g
P
(
x
)
−
l
o
g
Q
(
x
)
]
=E_{x\sim p}[log{P(x)}-log{Q(x)}]
=Ex∼p[logP(x)−logQ(x)]
=
∑
i
=
1
N
P
(
x
i
)
[
l
o
g
P
(
x
i
)
−
l
o
g
Q
(
x
i
)
]
=\sum_{i=1}^NP(x_i)[log{P(x_i)}-log{Q(x_i)}]
=i=1∑NP(xi)[logP(xi)−logQ(xi)]
=
∑
i
=
1
N
P
(
x
i
)
l
o
g
P
(
x
i
)
−
∑
i
=
1
N
P
(
x
i
)
l
o
g
Q
(
x
i
)
=\sum_{i=1}^NP(x_i)log{P(x_i)}-\sum_{i=1}^NP(x_i)log{Q(x_i)}
=i=1∑NP(xi)logP(xi)−i=1∑NP(xi)logQ(xi)
=
H
(
P
,
Q
)
−
H
(
P
)
(4)
=H(P,Q)-H(P)\tag{4}
=H(P,Q)−H(P)(4)
公式4是相对熵的展开。通过公式4可以最后得到:
H
(
P
,
Q
)
=
D
K
L
(
P
,
Q
)
+
H
(
P
)
H(P,Q)=D_{KL}(P,Q)+H(P)
H(P,Q)=DKL(P,Q)+H(P)
当在机器学习要优化交叉熵的时候,实际上是优化相对熵,因为
H
(
P
)
H(P)
H(P)是训练集自带的,无法改变和优化,是一个常数。所以在PyTorch中计算交叉熵损失是下面这样:

其中xi已经取出来了,所以概率就是1,P(xi)是1,这里是求单个样本的交叉熵,所以求和项也是没有的
伯努利二分布的熵的图像

2、nn.NLLLoss
功能:实现负对数似然函数中的负号功能
主要参数:
·weight:各类别的loss设置权值
·ignore_index:忽略某个类别
·reduction:计算模式,可为none/sum/mean
none-逐个元素计算
sum-所有元素求和,返回标量
mean-加权平均,返回标量
3、nn.BCELoss
功能:二分类交叉熵
注意事项:输入值取值在[0,1]
主要参数:
·weight:各类别的loss设置权值。
·ignore_index:忽略某个类别
·reduction:计算模式,可为none/sum/mean
none-逐个元素计算
sum-所有元素求和,返回标量
mean-加权平均,返回标量
熟悉的损失函数:
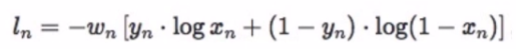
4、nn.BCEWithLogitsLoss
功能:结合Sigmoid与二分类交叉熵
注意事项:网络最后不加sigmoid函数
主要参数:
·pos_weight:正样本的权值
·weight:各类别的loss设置权值
·ignore_index:忽略某个类别
·reduction:计算模式,可为none/sum/mean
none-逐个元素计算
sum-所有元素求和,返回标量
mean-加权平均,返回标量
比上面的损失函数多了一个sigma
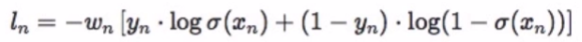























 568
568











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










