CS224W摘要14.Traditional Generative Models for Graphs

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
这节和下节都是讲图的生成模型，这节讲传统方法，下节讲DL方法。
之前学习的内容都是给定图，然后学习这个图的特征，做特定的预测节点、边等任务：

这节开始研究如何用模型生成这样的图。

几个好处：
Insights – We can understand the formulation of graphs
Predictions – We can predict how will the graph further evolve
Simulations – We can use the same process to general novel graph instances
Anomaly detection - We can decide if a graph is normal / abnormal

这块图生成模型分三块来讲，第一块先复习真实图的基本属性；第二块学习传统图生成模型；第三块学习深度图生成模型（下节讲）。

Properties of Real-world Graphs

这块基本属于复习，基本前面都有讲过这些内容（Lecture 1&2）。
Degree distribution: $P(k)$
Clustering coefficient: $C$
Connected components: $s$
Path length: $h$

Degree distribution

记随机选择的节点拥有度为$k$的概率：$P(k)$
记有$N_k$个节点拥有度为$k$，则：
$$P(k)=\frac{N_k}{N}$$

Clustering coefficient

聚集系数，用来衡量节点$i$的邻居的相互连接程度，记节点$i$的度为$k_i$，则聚集系数为：
$$C_i=\frac{2e_i}{k_i(k_i-1)},C_i\in [0,1]$$

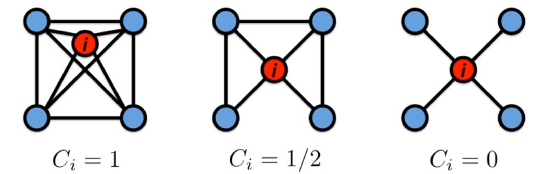
$e_i$是邻居之间的边，不含节点$i$与邻居的边。
整个图的聚集系数是求所有节点的聚集系数后进行平均：
$$C=\frac{1}{N}\sum _i^N{C}_i$$

Connectivity

就是最大连通分量，找出下图的最大连通分量：

步骤：
1.从随机一个节点开始做BFS
2.标记访问过的节点
3.如果所有节点均能访问，则该图是连通图
3.1否则重新找一个未访问的节点从步骤1开始，直到所有图中节点都被访问。

Path Length

图的直径：图中任意节点对的最大的最短路径长度
对于连通无向图或强连通有向图而言，图的平均路径长度为：
$$\bar{h}=\frac{1}{2E_{\max }}\sum _{i,j\ne i}{h}_{ij}$$
其中$h_{ij}$是两个节点之间的距离，$E_{\max }=n(n-1)/2$是图中可包含的最大边数量。
通常在计算过程中，我们会忽略掉路径长度为无穷的值，从而计算出正确的平均路径长度。

有了上面四个属性，下面来看具体实际图的例子。

MSN Graph

MSN Messenger: 只包含 1 month of activity，基本信息如下：
245 million users logged in
180 million users engaged in conversations
More than 30 billion conversations
More than 255 billion exchanged messages

原始度分布，平均度为14.4：

横纵坐标log后的度分布

聚集系数：0.114

连通分量，最大那个基本涵盖99%的用户。

路径长度，平均路径长度为6.6,90%的节点可以在8跳内相互访问。

以上信息没有对比也无法知道这些指标是否偏高或者正常，下面引入三个生成随机图的方法，将生成图与MSN网络进行对比。

Erdös-Renyi Random Graphs

这个方法是两个发明人的名字合体命名的。类似RAS，它有两种形式：
$G_{np}$：表示一个有$n$个节点的无向图，其中每个节点对$(u,v)$是否有边，是按i.i.d.（独立同分布）的概率$p$进行设置的。
$G_{nm}$：表示一个有$n$个节点的无向图，其中随机选择$m$个节点对形成边。
主要看第一种形式。它有两个变量来控制生成图的形式：

下面来看$G_{np}$生成的图的几个属性：

Degree distribution of $G_{np}$

其度分布是一个二项分布：

上面的$n-1$表示是除了当前节点外，从$n-1$个节点中选出$k$个节点，让这$k$个节点与当前节点以概率$p$的方式相连。
该二项分布的均值和方差为：
$$\begin{gathered} \bar{k}=p(n-1) \\ \sigma =p(1-p)(n-1) \end{gathered}$$
看图基本就是高斯分布：

Clustering Coefficient of $G_{np}$

由于图中的边是按i.i.d.（独立同分布）的概率$p$进行设置的。因此，对于节点$i$度为$k_i$而言，其邻居之间出现边的期望可以表示为：
$$E[e_i]=p\frac{k_i(k_i-1)}{2}$$
从而根据原始的聚集系数公式得到期望聚集系数为：
$$E[C_i]=\frac{p\cdot k_i(k_i-1)}{k_i(k_i-1)}=p=\frac{\bar{k}}{n-1}\approx \frac{\bar{k}}{n}$$
上式中最后的等号由均值公式转化得来。
随机图的聚集系数比较小，如果用固定的度$k或者p=k\cdot 1/n$来生成图，随着图节点数$n$越大，聚集系数越小。

$G_{np}$的连通分量

保证图中节点数量不变，将生成边的概率从0变到1，图结构则有下面的变化：

看两头：
当$p=0$，表示不会有边生成，空图
当$p=1$，表示每个节点对100%生成边，完全图
$\bar{k}=p(n-1)$，因此当$p=\frac{1}{n-1}$时，$\bar{k}=1$，意味每个节点都会有一条边相连，意味着开始出现较大连通分量，如果边小于节点数量，也就是$\bar{k}<1$时，意味着有节点是没有边相连的。基于这个理论，我们可以得到giant component:出现的临界点就是节点平均度为1，写成数学表达就是：
$$\bar{k}=\frac{2E}{n}\text{ or }p=\frac{\bar{k}}{(n-1)}$$
当节点平均度小于1时：$k=1-\epsilon$，所有连通分量大小上限是（原文是所有连通分量大小都是，感觉不对）：$\Omega (\log n)$

当节点平均度大于1时：$k=1+\epsilon$，有一个连通分量大小上限是：$\Omega (n)$，其他连通分量大小上限是：$\Omega (\log n)$
此时每个节点的期望边数至少为1，在可视化后就是：

这个图也对应了上一张图的理论推断，可以看到，平均度大于1时，最大连通量中的节点急剧增加，当平均度为2的时候，80%的节点都在最大连通分量中了。

Expansion

这里补充一个图$G(V,E)$的扩展系数$\alpha$：
$$\alpha =\underset{S\subseteq V}{\min }\frac{\text{\# edges leaving S}}{\min (|S|,|V\setminus S|)}$$
看图：

中间黑线就是$\text{\# edges leaving S}$
扩展系数用来衡量一个图的鲁棒性，要断开$l$个节点，需要去掉$\ge \alpha \cdot l$条边。

上面的几个图例中，真实图一般介于第一和第二个之间。社区内部鲁棒性强，社区间的鲁棒性差。
这个新的定义和下面要将的路径长度有关。
定理：对于一个包含$n$个节点的图，若其扩展系数为$\alpha$则所有节点对的（平均?有点类似计算时间复杂度的味道）路径长度为：
$$O(\frac{\log n}{\alpha })$$
也就是说，当图规模变大，那么$\log n$会变大，但同时$\alpha$也会变大，因此路径长度相对而言不一定会变大。
对于一个随机图$G_{np}$，存在以下关系：
$$\log n>np>c(常数)$$
其直径为：
$$diam(G_{np}=O(\frac{\log n}{\log (np)}))$$
从上面的式子可以知道，随机图$G_{np}$的直径是节点数量的对数，因此随机图$G_{np}$有比较好的扩展性，可以在对数级步数内BFS所有节点

Shortest Path of $G_{np}$

有了上面扩展系数的基础，我们可以知道，$G_{np}$随机图可以在拥有很大规模的情况下，仍然保持很短的最短路径（图直径很小）。
当我们将节点的平均度设置不变：$\bar{k}=np=常数$
那么$G_{np}$的直接就变成：
$$diam(G_{np}=O(\log n)$$
实验可以证明：

MSN vs $G_{np}$

偷懒做表，直接上图：

通过上面的对比实际图与$G_{np}$随机图的共同点在于：
Giant connected component
Average path length
不同点在于：
Clustering Coefficient，随机图聚集系数非常低
Degree Distribution，随机图度分布是二项分布
下面看第二种随机图生成方法。

The Small-World Model

通过上节的学习我们看到，$G_{np}$随机图两种平均路径长度较长（$o(\log n)\approx 8.2$），聚集系数较低（$\frac{\bar{k}}{n}\approx 8\cdot 10^{-8}$）。

我们希望找到一种高聚集系数且平均路径较短的随机图，使其更接近真实图。

因为在相同平均节点度的情况下，真实图比起随机图而言，平均路径较短（其实差不多），聚集系数更大

一般来说，平均路径和聚集系数两个不可同时得到，因此要想在二者之间做trade off，就是Small-world graph的思想：

创建步骤

(1) Start with a low-dimensional regular lattice（这里用环形代替lattice）
此时的图拥有高聚集系数

(2) Rewire: Introduce randomness (“shortcuts”)
重新连接节点对，对每个节点对，以概率$p$将其终点重新接到另外的随机节点上。

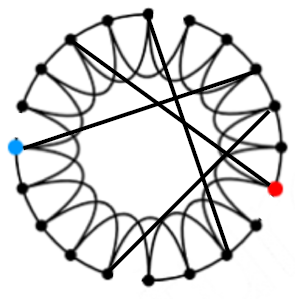
结果及分析

可以看到随着随机rewire的概率$p$趋近1，中间状态就是我们的目标网络结构。把聚集系数画出来：

可以看到当随机rewire概率趋向于1的时候，聚集系数才会变很小，但是很小随机rewire概率，就可以获得很多shortcut，使得平均路径变短。
注意看上图中的横坐标不是等值的。

小结

只需要很少的rewire操作，就可以让随机图获得较高的聚集系数，使其比较接近真实图，但是其度分布却不正确（这里应该补个图才有说服力）。

Kronecker Graph Model

第三种生成随机图的方式，是用recursive的方式来生成图结构。

具体方法是先根据给定的小矩阵$K_1$，通过克罗内克积得到$K_2=K_1\otimes K_1$

当然可以重复以上步骤：

上面提到的两个矩阵的克罗内克积定义如下：
$$C=A\otimes B\doteq \left(\begin{array}{cccc}{\alpha }_1{,}_{1}B& {\alpha }_1{,}_{2}B& \cdots & {\alpha }_1{,}_{m}B\\ {\alpha }_2{,}_{1}B& {\alpha }_2{,}_{2}B& \cdots & {\alpha }_2{,}_{m}B\\ ⋮& ⋮& \ddots & ⋮\\ {\alpha }_n{,}_{1}B& {\alpha }_n{,}_{2}B& \cdots & {\alpha }_n{,}_{m}B\end{array}\right)$$
其中A的维度是$N\times M$，B的维度是$K\times L$
最后结果的维度是：$(N\times K)\times (M\times L)$
两个图的克罗内克积就是图邻接矩阵的克罗内克积。
Kronecker graph is obtained by growing sequence of graphs by iterating the Kronecker product over the initiator matrix $K_1$:
$$K^{[m]}=K_m=\underset{\text{m }times}{\underbrace{K_1\otimes K_1\otimes \cdots K_1}}=K_{\text{m}-1}\otimes K_1$$

生成步骤

先定义初始化矩阵，initiator matrix，初始化矩阵可以包含多个矩阵，initiator
matrices：$K_1^{\prime },K_1^{\prime \prime },K_1^{\prime \prime \prime }$，这些不同矩阵大小可以不一样。
例如：


上面有两组不同的图，图的邻接矩阵，3次克罗内克积结果：$K_3$。
具体创建Stochastic Kronecker graphs步骤如下：
1.创建$N_1\times N_1$概率矩阵${\Theta }_1$
2.计$k^{th}$的Kronecker 积${\Theta }_k$
3.对于最后的结果${\Theta }_k$中的每个元素$p_{uv}$代表$K_k$有$p_{uv}$的概率生成边$(u,v)$

快速版生成步骤

上面的步骤中，如果得到了生成有向边的概率矩阵，要对矩阵中的$n^2$个元素依次生成边，相当于计算了$n^2$次，可以用另外一种快速生成方式，时间复杂度为边的线性复杂度$O(E)$。

丢边法（edge dropping，看着我翻译的土鳖名。。。百度了一下，有叫掉边法）：

上图中间是正常计算结果，右边是把结果看成四个小块，相当于原$\Theta$

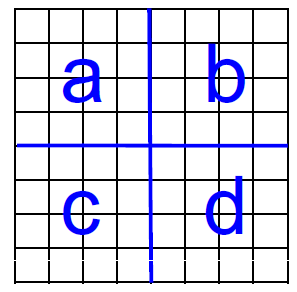
里面每个元素可以继续分，直到不能分解：

具体描述如下：
Fast Kronecker generator algorithm，针对生成有向图。
在有$n=2^m$个节点的图$G$中插入一条边，步骤如下：
1.创建归一化矩阵：
$$L_{uv}=\frac{{\Theta }_{uv}}{{\sum }_{op}{\Theta }_{op}}$$
2.For $i=1\cdots m$
2.1 从$x=0,y=0$开始
2.2 概率$L_{uv}$选择对应的象限$(u,v)$
2.3将象限进行分解，直到对应图$G$中的第$i$个元素：
$$x+=u\cdot 2^{m-i},y+=v\cdot 2^{m-i}$$
3.为图$G$添加边

其实比较晦涩难懂，可以这样想，上面步骤中的$m$就是克罗内克积的次数，就是把矩阵分形了多少次，最终结果可以根据初始化矩阵和$m$直接用公式算出来，如果一个图有$E$条边，直接算$E$次即可，所以全图生成时间复杂度为$O(E)$。

这种生成方式可能会在两个节点生成多条边，因为在2.2可能选择到相同结果。
贴一个原文的讲解：
https://blog.csdn.net/weixin_45443685/article/details/105738453
Kronecker和真实图比较像，实验结果不贴了。

总结

讲了三种传统随机图生成方式，这三种方式对生成图的过程有先验条件假设。