10.1近邻学习
k近邻(k-Nearest Neighbor,简称kNN)学习是一种常用的监督学习方法,其原理是:给定测试样本,找出训练集中与其最靠近的k个训练样本(基于距离度量方式),然后基于这K个“邻居”的信息来进行预测。是一种常用的监督学习方法。
- 在分类任务中,使用“投票法”,即选择k个样本中出现最多的类别标记作为预测结果。
在回归任务中,使用“平均法”,将这k个样本的实值输出标记的平均值作为预测结果。也可基于距离远近进行加权平均或加权投片,距离越近的样本权重越大。
k近邻学习方法:没有显示的训练过程,是懒惰学习(lazy learning),在训练阶段仅把样本保存起来,训练时间开销为零,待收到测试样本后在进行处理;相对应急切学习(eager learning)而言,就是在训练阶段就对样本进行学习处理的方法。
k近邻分类器中,k为不同值时,分类结果也就不同;同时,若采用不同的距离计算方式,则找出的近邻也有显著差别,导致分类结果也显著不同。假设距离计算是恰当的,就是不考虑距离导致的差异性,而就从k这个参数的差异就最近邻分类器在二分类问题上的性能进行分析。
10.2低维嵌入
k近邻学习方法基于一个重要的假设,任意测试样本x附近任意小的d距离范围内总能找到一个训练样本,即训练样本的采样密度足够大(密采样dense sample)。在现实中这个假设很难满足。
eg:当d=0.001,则仅需要1000个测试样本点平均分布在归一化后的属性取值范围内,才可以使得任意测试样本在其附近0.001距离范围内总能找到一个训练样本。此时满足10.1所描述的错误率。这紧紧是k=1的情形。
若k=20,采用密采样,则需要
在高维情形下,样本数的采样以及距离计算问题。在高维情形下出现的数据样本稀疏、距离计算困难等问题,是所有机器学习方法共同面临的严重障碍,被称为维数灾难(curse of dimensionality)。
缓解维数灾难的两个途径:
- 特征选择;
- 降维(dimension reduction)。
思路上,这两种途径都是减少维数,不过一个是在事前,一个是在事中。降维,也称维数约简,通过某种数学变换将原始高维属性空间转变为一个低维子空间(subspace),在子空间中,样本密度可以大幅提高,距离计算也相对容易。事实上,观测或收集到的数据样本虽然是高维的,但与学习任务相关的或许只是某个低维分布,这也是特征选择可以事前根据业务来定义的。
为什么可以降维?降维后的是否影响样本距离呢?降维后要求样本空间中样本之间的距离在低维空间中得以保持,多维缩放(multiple dimensional scaling,MDS)是一种经典的降维方法。
对降维效果的评估,通常是比较降维前后学习器的性能,若性能有所提高,则认为降维起到了作用。若将维数降至二维或三维,则可通过可视化技术来直观地判断降维效果。
一般来说要获得低维子空间,最简单的是对原始高维空间进行线性变换。个人想法:这个线性变换的过程在机器学习领域十分的常见,无论是线性回归算法、支持向量机还是神经网络都有用到线性变换。以神经网络来比喻我们这里的降维算法,将 d 维的属性样本降维到 d’ 维的属性空间上,其实等同为输入神经元为 d 个、输出神经元为 d’ 个的浅层神经网络结构,借用一下第五章的图解释一下

降维后的每个新的属性 x’ 其实是高维属性 x1、x2、…、xn 根据权重 W 的线性组合。这种基于线性变换进行降维的方法称为线性降维方法,对低维子空间的性质有不同的要求,相对于对权重 W 施加了不同的约束。对降维效果的评估,通常是比较降维前后学习器的性能,若性能提升了则认为降维起到了效果。
10.3主成分分析
思路:主成分分析、Principal Component Analysis、PCA的推导有很多种途径,我们选择一种容易理解的来讲解,目的是降维。

我们画的是二维情况,但是具体到高维也是可以的。μ是我们目测一个比较好的降维之后的投影方向。但是这只是目测,我们怎么规定这个准则呢?我们规定:
投影之后样本竟可能分散,即样本方差尽可能大。
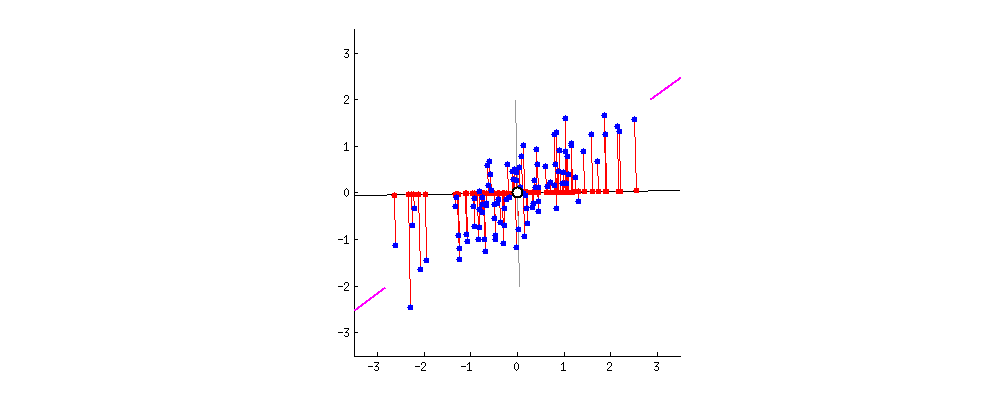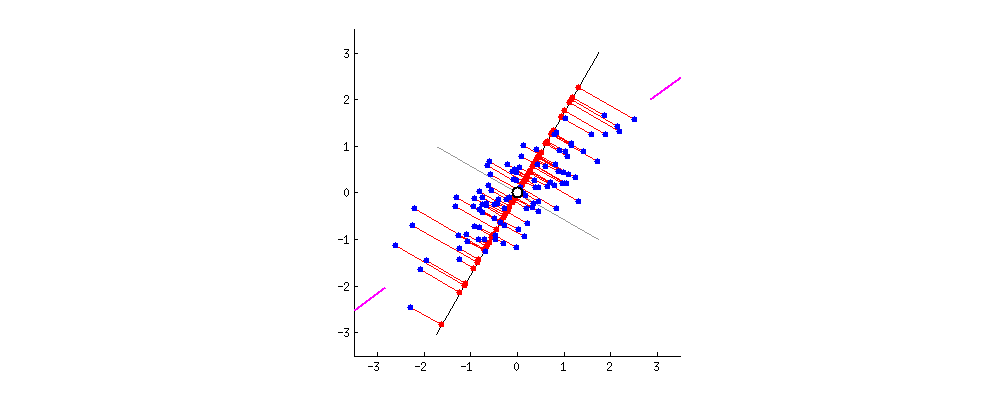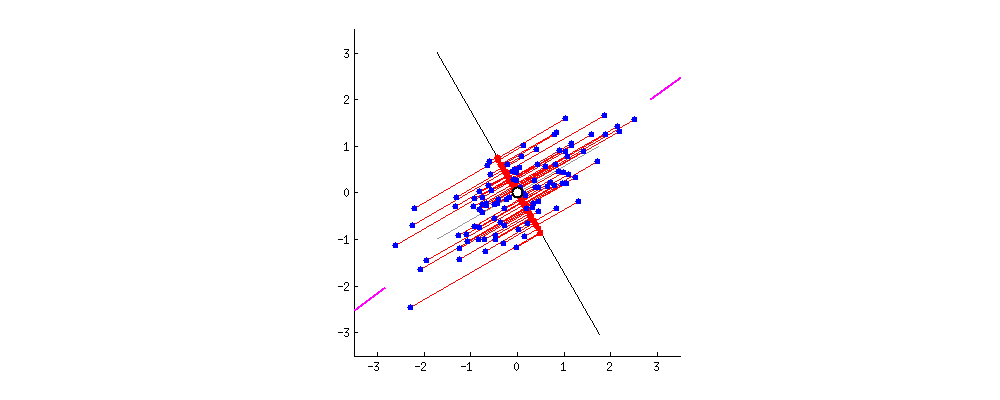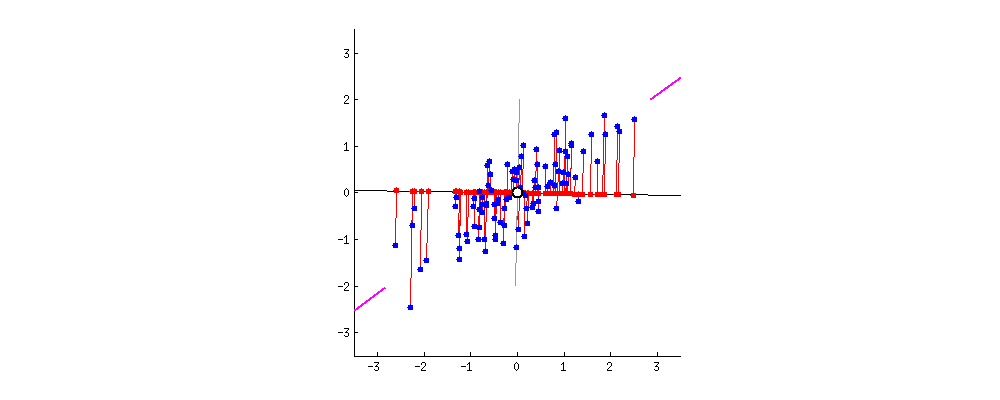
PCA的目的:
PCA是一种在尽可能减少信息损失的情况下找到某种方式降低数据的维度的方法。通常来说,我们期望得到的结果,是把原始数据的特征空间(n个d维样本)投影到一个小一点的子空间里去,并尽可能表达的很好(就是说损失信息最少)。常见的应用在于模式识别中,我们可以通过减少特征空间的维度,抽取子空间的数据来最好的表达我们的数据,从而减少参数估计的误差。注意,主成分分析通常会得到协方差矩阵和相关矩阵。这些矩阵可以通过原始数据计算出来。协方差矩阵包含平方和与向量积的和。相关矩阵与协方差矩阵类似,但是第一个变量,也就是第一列,是标准化后的数据。如果变量之间的方差很大,或者变量的量纲不统一,我们必须先标准化再进行主成分分析。
PCA的过程:
1.去掉数据的类别特征(label),将去掉后的d维数据作为样本
2.计算d维的均值向量(即所有数据的每一维向量的均值)
3.计算所有数据的散布矩阵(或者协方差矩阵)
4.计算特征值(e1,e2,…,ed)以及相应的特征向量(lambda1,lambda2,…,lambda d)
5.按照特征值的大小对特征向量降序排序,选择前k个最大的特征向量,组成d*k维的矩阵W(其中每一列代表一个特征向量)
6.运用d*K的特征向量矩阵W将样本数据变换成新的子空间。(用数学式子表达就是y=w^t*x,其中x是d*1维的向量,代表一个样本,y是K*1维的在新的子空间里的向量)
1.数据准备—-生成三维样本向量
首先随机生成40*3维的数据,符合多元高斯分布。假设数据被分为两类,其中一半类别为w1,另一半类别为w2
#coding:utf-8
import numpy as np
np.random.seed(4294967295)
mu_vec1 = np.array([0,0,0])
cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20).T
assert class1_sample.shape == (3,20)#检验数据的维度是否为3*20,若不为3*20,则抛出异常
mu_vec2 = np.array([1,1,1])
cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]])
class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20).T
assert class1_sample.shape == (3,20)#检验数据的维度是否为3*20,若不为3*20,则抛出异常
2.作图查看原始数据的分布
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111, projection='3d')
plt.rcParams['legend.fontsize'] = 10
ax.plot(class1_sample[0,:], class1_sample[1,:], class1_sample[2,:], 'o', markersize=8, color='blue', alpha=0.5, label='class1')
ax.plot(class2_sample[0,:], class2_sample[1,:], class2_sample[2,:], '^', markersize=8, alpha=0.5, color='red', label='class2')
plt.title('Samples for class 1 and class 2')
ax.legend(loc='upper right')
plt.show()结果:

3.去掉数据的类别特征
1 all_samples = np.concatenate((class1_sample, class2_sample), axis=1)
2 assert all_samples.shape == (3,40)#检验数据的维度是否为3*20,若不为3*20,则抛出异常4.计算d维向量均值
mean_x = np.mean(all_samples[0,:])
mean_y = np.mean(all_samples[1,:])
mean_z = np.mean(all_samples[2,:])
mean_vector = np.array([[mean_x],[mean_y],[mean_z]])
print('Mean Vector:\n', mean_vector)结果:
1 print('Mean Vector:\n', mean_vector)
2 Mean Vector:,
3 array([[ 0.68047077],
4 [ 0.52975093],
5 [ 0.43787182]]))5.计算散步矩阵或者协方差矩阵
a.计算散步矩阵
散布矩阵公式:
其中m是向量的均值:
(第4步已经算出来是mean_vector)
1 scatter_matrix = np.zeros((3,3))
2 for i in range(all_samples.shape[1]):
3 scatter_matrix += (all_samples[:,i].reshape(3,1) - mean_vector).dot((all_samples[:,i].reshape(3,1) - mean_vector).T)
4 print('Scatter Matrix:\n', scatter_matrix)结果:
1 print('Scatter Matrix:\n', scatter_matrix)
2 ('Scatter Matrix:,
3 array([[ 46.81069724, 13.95578062, 27.08660175],
4 [ 13.95578062, 48.28401947, 11.32856266],
5 [ 27.08660175, 11.32856266, 50.51724488]]))b.计算协方差矩阵
如果不计算散布矩阵的话,也可以用python里内置的numpy.cov()函数直接计算协方差矩阵。因为散步矩阵和协方差矩阵非常类似,散布矩阵乘以(1/N-1)就是协方差,所以他们的特征空间是完全等价的(特征向量相同,特征值用一个常数(1/N-1,这里是1/39)等价缩放了)。协方差矩阵如下所示:

cov_mat = np.cov([all_samples[0,:],all_samples[1,:],all_samples[2,:]])
print('Covariance Matrix:\n', cov_mat)结果:
1 >>> print('Covariance Matrix:\n', cov_mat)
2 Covariance Matrix:,
3 array([[ 1.20027429, 0.35784053, 0.69452825],
4 [ 0.35784053, 1.23805178, 0.29047597],
5 [ 0.69452825, 0.29047597, 1.29531397]]))6.计算相应的特征向量和特征值
# 通过散布矩阵计算特征值和特征向量
eig_val_sc, eig_vec_sc = np.linalg.eig(scatter_matrix)
# 通过协方差矩阵计算特征值和特征向量
eig_val_cov, eig_vec_cov = np.linalg.eig(cov_mat)
for i in range(len(eig_val_sc)):
eigvec_sc = eig_vec_sc[:,i].reshape(1,3).T
eigvec_cov = eig_vec_cov[:,i].reshape(1,3).T
assert eigvec_sc.all() == eigvec_cov.all()
print('Eigenvector {}: \n{}'.format(i+1, eigvec_sc))
print('Eigenvalue {} from scatter matrix: {}'.format(i+1, eig_val_sc[i]))
print('Eigenvalue {} from covariance matrix: {}'.format(i+1, eig_val_cov[i]))
print('Scaling factor: ', eig_val_sc[i]/eig_val_cov[i])
print(40 * '-')结果:
Eigenvector 1:
[[-0.84190486]
[-0.39978877]
[-0.36244329]]
Eigenvalue 1 from scatter matrix: 55.398855957302445
Eigenvalue 1 from covariance matrix: 1.4204834860846791
Scaling factor: 39.0
----------------------------------------
Eigenvector 2:
[[-0.44565232]
[ 0.13637858]
[ 0.88475697]]
Eigenvalue 2 from scatter matrix: 32.42754801292286
Eigenvalue 2 from covariance matrix: 0.8314755900749456
Scaling factor: 39.0
----------------------------------------
Eigenvector 3:
[[ 0.30428639]
[-0.90640489]
[ 0.29298458]]
Eigenvalue 3 from scatter matrix: 34.65493432806495
Eigenvalue 3 from covariance matrix: 0.8885880596939733
Scaling factor: 39.0
----------------------------------------其实从上面的结果就可以发现,通过散布矩阵和协方差矩阵计算的特征空间相同,协方差矩阵的特征值*39 = 散布矩阵的特征值
当然,我们也可以快速验证一下特征值-特征向量的计算是否正确,是不是满足方程
(其中为伊布西农为协方差矩阵,v为特征向量,lambda为特征值)
可视化特征向量
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import proj3d
from matplotlib.patches import FancyArrowPatch
class Arrow3D(FancyArrowPatch):
def __init__(self, xs, ys, zs, *args, **kwargs):
FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs)
self._verts3d = xs, ys, zs
def draw(self, renderer):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
self.set_positions((xs[0],ys[0]),(xs[1],ys[1]))
FancyArrowPatch.draw(self, renderer)
fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111, projection='3d')
ax.plot(all_samples[0,:], all_samples[1,:], all_samples[2,:], 'o', markersize=8, color='green', alpha=0.2)
ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5)
for v in eig_vec_sc.T:
a = Arrow3D([mean_x, v[0]], [mean_y, v[1]], [mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r")
ax.add_artist(a)
ax.set_xlabel('x_values')
ax.set_ylabel('y_values')
ax.set_zlabel('z_values')
plt.title('Eigenvectors')
plt.show()结果:

我们的目标是减少特征空间的维度,即通过PCA方法将特征空间投影到一个小一点的子空间里,其中特征向量将会构成新的特征空间的轴。然而,特征向量只会决定轴的方向,他们的单位长度都为1,可以用代码检验一下:
for ev in eig_vec_sc:
numpy.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev))因此,对于低维的子空间来说,决定丢掉哪个特征向量,就必须参考特征向量相应的特征值。通俗来说,如果一个特征向量的特征值特别小,那它所包含的数据分布的信息也很少,那么这个特征向量就可以忽略不计了。常用的方法是根据特征值对特征向量进行降序排列,选出前k个特征向量
# 生成(特征向量,特征值)元祖
eig_pairs = [(np.abs(eig_val_sc[i]), eig_vec_sc[:,i]) for i in range(len(eig_val_sc))]
#对(特征向量,特征值)元祖按照降序排列
eig_pairs.sort(key=lambda x: x[0], reverse=True)
#输出值
for i in eig_pairs:
print(i[0])结果:
1 84.5729942896
2 39.811391232
3 21.22757606828.选出前k个特征值最大的特征向量
前面所讲的是想把三维的空间降维成二维空间,现在我们把前两个最大特征值的特征向量组合起来,生成d*k维的特征向量矩阵W
1 matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1)))
2 print('Matrix W:\n', matrix_w)结果:
1 >>> print('Matrix W:\n', matrix_w)
2 Matrix W:,
3 array([[-0.62497663, 0.2126888 ],
4 [-0.44135959, -0.88989795],
5 [-0.643899 , 0.40354071]]))9.将样本转化为新的特征空间
最后一步,把2*3维的特征向量矩阵W带到公式 中,将样本数据转化为新的特征空间
中,将样本数据转化为新的特征空间
matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1)))
print('Matrix W:\n', matrix_w)
transformed = matrix_w.T.dot(all_samples)
assert transformed.shape == (2,40), "The matrix is not 2x40 dimensional."
plt.plot(transformed[0,0:20], transformed[1,0:20], 'o', markersize=7, color='blue', alpha=0.5, label='class1')
plt.plot(transformed[0,20:40], transformed[1,20:40], '^', markersize=7, color='red', alpha=0.5, label='class2')
plt.xlim([-4,4])
plt.ylim([-4,4])
plt.xlabel('x_values')
plt.ylabel('y_values')
plt.legend()
plt.title('Transformed samples with class labels')
plt.show()结果:

10.4流行学习
流行学习(manifold learning)是一类借鉴了拓扑流行概念的降维方法。“流行”是在局部与欧式空间同胚的空间。换言之,它在局部具有欧式空间的性质,能用欧式距离来进行距离计算。
等度量映射认为高维空间的直线距离,并不能很好的表现样本之间的距离。如下图所示:

高维空间中的AB直线距离并不准确,反而绿色的线的长度作为长度看起来更靠谱。这个低维嵌入流行上两点的距离是“测地线”(geodesic)距离。
我们可以对于每一个点基于欧式距离找出其临近点来计算测地线,然后就能建立一个近邻连接图,图中近邻点之间存在连接,非近邻点不存在连接。于是计算测地线距离的问题,就变换为计算近邻图上两点之间的最短路径问题(这是一个很好的近似~)。
这里有著名算法Dijkstra或Floyd算法。
Dijkstra

Floyd
Floyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
算法思想原理:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k算法描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。 之后就变成普通的低维嵌入了。
10.5一种常用的非线性降维方法:核化线性降维
在现实任务中,有时候直接使用线性降维会导致部分信息丢失的,本书举的例子是基于这样的一个场景,低维空间映射到高维空间后,再次降维到低维空间会导致原始的低维结构丢失。

核化线性降维的本质是基于核技巧对线性降维方法进行“核化”(kernelized),以前边的主成分分析法线性降维为例,核化主成分分析算法是在主成分分析的基础上将高维空间的样本投射 X 转换为被核化的 k(X) 来进行计算,并对核函数对应的核矩阵进行特征分解来求得投影的 d维特征向量
10.6度量学习(metric learning)
在机器学习中,对高维数据进行降维的主要目的是希望找到一个合适的低维空间,在此空间进行学习能比原始空间要好。事实上,每个空间对应了在样本属性上定义的一个合适的距离度量。那么,何不直接尝试“学习”出一个合适的距离度量呢?这就是度量学习的基本动机
欲对距离度量进行学习,我们需要为样本之间的距离计算加上权重,并可以根据具体样本来对权重进行训练,这个权重构成的矩阵我们称为“度量矩阵”。
度量学习的目的就是计算出合适的“度量矩阵”,在实际计算时,我们可以将度量矩阵 M 直接嵌入到近邻分类器的评价体系中去,通过优化该性能指标相应的求得 M.
2. 基础知识
1)懒惰学习(lazy learning)
此类学习技术在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理
2)急切学习(eager learning)
与懒惰学习相反,此类学习技术在训练阶段就对样本进行学习处理
3)维度灾难(curse of dimensionality)
在高维情形下出现的样本稀疏、距离计算困难等问题,是所有机器学习方法共同面临的严重障碍,被称为“维度灾难”
4)矩阵的迹(trace)
在线性代数中,一个n×n矩阵A的主对角线(从左上方至右下方的对角线)上各个元素的总和被称为矩阵A的迹(或迹数),一般记作tr(A)。
5)矩阵特征分解(Eigenvalue decomposition)
将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解。简单理解就是将矩阵变换为几个相互垂直的向量的和,比如在二维空间中,任意一个向量可以被表示为x轴和y轴的组合。
3. 总结
1)k 近邻学习是简单常用的分类算法,在样本分布充足时,其最差误差不超过贝叶斯最优分类器的两倍
2)实际情况下由于属性维度过大,会导致“维数灾难”,这是所有机器学习中的共同障碍
3)缓解维数灾难的有效途径是降维,即将高维样本映射到低维空间中,这样不仅属性维度降低减少了计算开销,还增大了样本密度
4)降维过程中必定会对原始数据的信息有所丢失,所以根据不同的降维目标我们可以得到不同的降维方法
5)多维缩放的目标是要保证降维后样本之间的距离不变
6)线性降维方法目标是要保证降维到的超平面能更好的表示原始数据
7)核线性降维方法目标是通过核函数和核方法来避免采样空间投影到高维空间再降维之后的低维结构丢失
8)等度量映射的目标是让样本在“流形”上的距离在降维之后仍能保持
9)局部线性嵌入的目标是让样本由其邻域向量重构关系在降维后仍能保持
10)度量学习绕过降维的过程,将学习目标转化为对距离度量计算的权重矩阵的学习有趣的小数据:宇宙间基本粒子的总数约为10的80次方,而一粒灰尘中含有几十亿基本粒子,而要满足k近邻算法假设的属性数量为20的样本数量为10的60次方。





























 3399
3399

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








