题目描述
Description
Input
输入的第一行包含两个正整数 n、m。 接下来 n行描述初始棋盘。其中第i 行包含 m个字符,每个字符都是大写英文字母"X"、大写英文字母"O"或点号"."之一,分别表示对应的棋盘格中有黑色棋子、有白色棋子和没有棋子。其中点号"."恰好出现一次。 接下来一行包含一个整数 k(1≤k≤1000) ,表示兔兔和蛋蛋各进行了k次操作。 接下来 2k行描述一局游戏的过程。其中第 2i – 1行是兔兔的第 i 次操作(编号为i的操作) ,第2i行是蛋蛋的第i次操作。每个操作使用两个整数x,y来描述,表示将第x行第y列中的棋子移进空格中。 输入保证整个棋盘中只有一个格子没有棋子, 游戏过程中兔兔和蛋蛋的每个操作都是合法的,且最后蛋蛋获胜。
Output
输出文件的第一行包含一个整数r,表示兔兔犯错误的总次数。 接下来r 行按递增的顺序给出兔兔“犯错误”的操作编号。其中第 i 行包含一个整数ai表示兔兔第i 个犯错误的操作是他在游戏中的第 ai次操作。 1 ≤n≤ 40, 1 ≤m≤ 40
Sample Input
样例一:
1 6
XO.OXO
1
1 2
1 1
样例二:
3 3
XOX
O.O
XOX
4
2 3
1 3
1 2
1 1
2 1
3 1
3 2
3 3
样例三:
4 4
OOXX
OXXO
OO.O
XXXO
2
3 2
2 2
1 2
1 3
Sample Output
1
1
样例二:
0
样例三:
2
1
2
样例1对应图一中的游戏过程
样例2对应图三中的游戏过程
HINT
分析
75分做法
我们把操作看做是空格在移动。
我们做这道题最先想到的就是,操作是否可能成环?
答案是否定的。我们假设环长为
n
,显然
既然不能成环,而且数据还这么小,似乎搜索很好写。敲一发,75分到手。
满分做法
我们发现,移动路径上,相邻两个点的颜色总是不一样的,这然我们想到了二分图。
我们在相邻而且颜色不相同的两个点之间连边,由于空格能够走到白色格子,我们不妨把空格看做黑色。
先手在当前点能够获胜的条件是从当前点出发,能够找到一条路径长度是奇数而且先手一定能够使路径长度为奇数。
由于是二分图,那我们求个最大匹配试试。
我们发现,匈牙利算法增广时的交错轨不就是一条长度为奇数的路径吗。
那么我们来思考一下两种情况。
如果当前点不一定最大匹配上,那么它的邻接点一定在最大匹配上。 我们假设它的邻接点不一定在最大匹配上:
- 存在邻接点不在时,当前点也不在。那么久可以增广了,和假设是最大匹配不符。
- 如果邻接点和当前点一定有一个在,那么邻接点和当前点一定还通过一个有偶数条边的交错轨相连,加上这条边就是一个奇环了,不是二分图。
如果当前点一定在最大匹配上,则一定获胜
首先,当前点一定在一条增广路径上,即在一条交错轨上。这条交错轨一定是奇数的,而且被这个点分成了一边是奇数,一边是偶数。但是奇数那一边也有可能有一条偶数的交错轨,即可能有岔路。
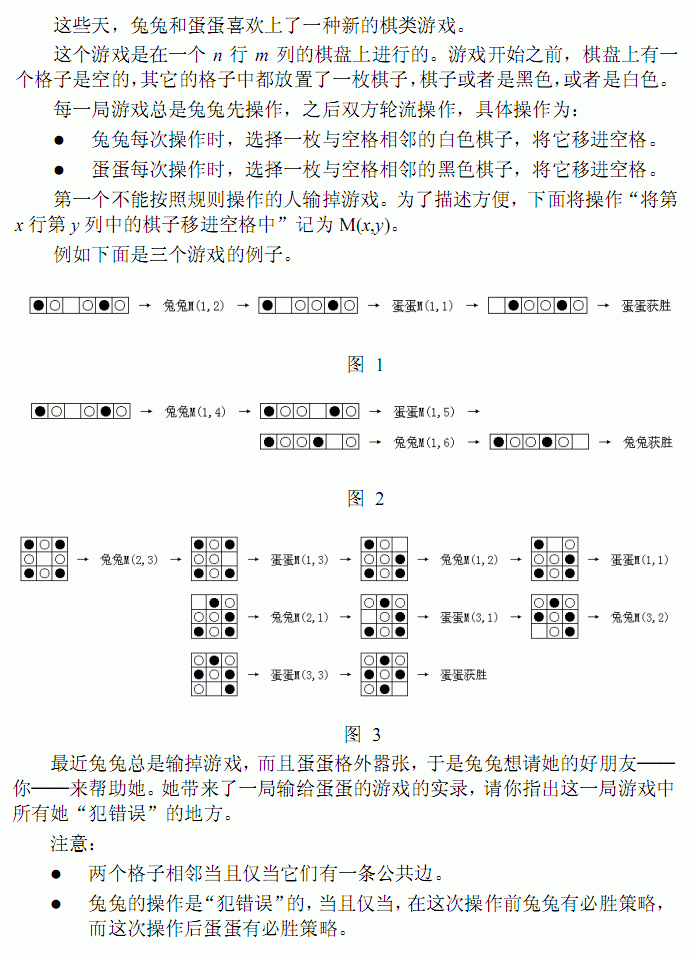
我们来分析一下,岔路可能有两种情况。
显然,这种情况你自己不去走那边就好了。- 出现在别人的节点
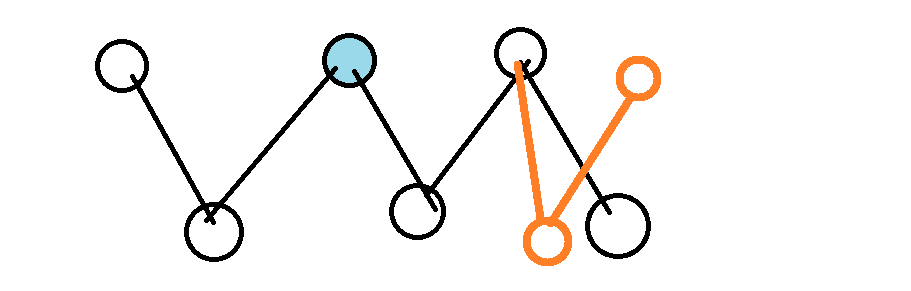
如果朝奇数条交错轨的方向走,自己的节点到别人的节点这条边应该在最大匹配中(图中蓝色的边),但是这条边显然可以被橙色的边代替,和当前点一定在最大匹配上的假设不符。
所以,最终一定走的是奇数条边,使后手无法行动。 也可以这么看,先手一定可以有边可走(沿着匹配边走),但是后手不一定有边可走。
- 出现在别人的节点
由此我们得出结论,如果先手所在的点在一定在最大匹配上,则先手有必胜策略,否则,后手有必胜策略。
每次操作时,我们就检查当前空格所在位置是不是一定在最大匹配上,然后将这个位置删掉,将空格的位置设置为这次操作的位置。
那么我们怎么看当前点是不是一定在最大匹配上呢?
- 如果当前点本来就没有匹配的点,显然不在。
- 如果当前点所匹配的点在删去当前点后,能够继续增广,就说明当前点不一定在最大匹配上,否则一定在。
代码
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
#define MAXN 40
#define MAXM 40
#define MAXK 1000
queue<int>q;
int n,m,cx[MAXN*MAXM+10],dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}},bx,by,cnt,ans[MAXK+10],k;
char s[MAXN+10][MAXN+10];
bool vis[MAXN*MAXM+10],ban[MAXN*MAXM+10];
struct node{
int v;
node *next;
}*adj[MAXN*MAXN+10],edge[MAXN*MAXN*4+10],*ecnt=edge;
inline void addedge(int u,int v){
node *p=++ecnt;
p->v=v;
p->next=adj[u];
adj[u]=p;
}
void Read(int &x){
static char c;
while(c=getchar(),c!=EOF)
if(c>='0'&&c<='9'){
x=c-'0';
while(c=getchar(),c>='0'&&c<='9')
x=x*10+c-'0';
ungetc(c,stdin);
return;
}
}
void read(){
Read(n),Read(m);
int i,j;
for(i=1;i<=n;i++)
scanf("%s",s[i]+1);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
if(s[i][j]=='O')
s[i][j]=0;
else if(s[i][j]=='X')
s[i][j]=1;
else
s[i][j]=1,bx=i,by=j;
}
inline int Get_id(int i,int j){
return (i-1)*m+j;
}
void bfs(){
q.push(Get_id(bx,by));
int u,x,y,tx,ty,v,d;
while(!q.empty()){
u=q.front();
q.pop();
x=(u+m-1)/m;
y=u-(x-1)*m;
for(d=0;d<4;d++){
tx=x+dir[d][0];
ty=y+dir[d][1];
if(tx&&ty&&tx<=n&&ty<=m&&s[x][y]^s[tx][ty]){
v=Get_id(tx,ty);
addedge(u,v);
if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
}
void print(){
printf("%d\n",cnt);
int i;
for(i=1;i<=cnt;i++)
printf("%d\n",ans[i]);
}
bool dfs(int u){
for(node *p=adj[u];p;p=p->next){
if(!vis[p->v]&&!ban[p->v]){
vis[p->v]=1;
if(!cx[p->v]||dfs(cx[p->v])){
cx[p->v]=u;
cx[u]=p->v;
return 1;
}
}
}
return 0;
}
void solve(){
int i,u,mt;
for(i=n*m;i;i--){
if(!cx[i]){
memset(vis,0,sizeof vis);
dfs(i);
}
}
bool r1,r2;
Read(k);
for(i=1;i<=k;i++){
u=Get_id(bx,by);
ban[u]=1;
if(cx[u]){
mt=cx[u];
cx[u]=cx[mt]=0;
memset(vis,0,sizeof vis);
r1=!dfs(mt);
}
else
r1=0;
Read(bx),Read(by);
u=Get_id(bx,by);
ban[u]=1;
if(cx[u]){
mt=cx[u];
cx[u]=cx[mt]=0;
memset(vis,0,sizeof vis);
r2=!dfs(mt);
}
else
r2=0;
if(r1&&r2)
ans[++cnt]=i;
Read(bx),Read(by);
}
}
int main()
{
read();
bfs();
solve();
print();
}
























 163
163

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








