随机变量的函数的数学期望

听海边涛声

已于 2023-12-28 19:25:27 修改

阅读量683

点赞数 5

文章标签：概率论

于 2023-12-28 19:06:24 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/panghuangang/article/details/135276310

版权

设 $Y$ 是随机变量 $X$ 的函数， $Y=g(X)$ （ $g$ 是连续函数）:

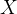$X$ 是离散型随机变量的情况

如果 $X$ 是离散型随机变量，它的分布律为

$P(X=x_{k})=p_{k}\; \; \; \; \; k=1,2,\cdots$

如果 $\sum_{k=1}^{\infty }g(x_{k})p_{k}$ 绝对收敛，则 $Y$ 的数学期望等于：

$E(Y)=E(g(X))=\sum_{k=1}^{\infty }g(x_{k})p_{k}\; \; \; \; \; \; \; (1)$

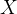$X$ 是连续型随机变量的情况

如果 $X$ 是连续型随机变量，它的分布律为 $f(x)$ ，如果

$\int_{-\infty }^{\infty }g(x)f(x)dx$

绝对收敛，那么 $Y$ 的数学期望等于：

$E(Y)=E(g(X))=\int_{-\infty }^{\infty }g(x)f(x)dx\; \; \; \; \; \; (2)$

两个或两个以上随机变量的函数的情况

设 $Z$ 是随机变量 $X,Y$ 的函数 $Z=g(X,Y)$ （ $g$ 是连续函数），那么 $Z$ 是一个一维随机变量。

若二维随机变量 $(X,Y)$ 是离散型型随机变量，其分布律为

$P(X=x_{i},Y=y_{j})=p_{ij},\; \; \; \; \; i,j=1,2,\cdots$

那么 $Z$ 的数学期望等于：

$E(Z)=E(g(X,Y))=\sum_{i=1}^{\infty }\sum_{j=1}^{\infty }g(x_{i},y_{j})p_{ij}\; \; \; \; \; \; \; (3)$

备注：假设上式右边的级数绝对收敛。

若二维随机变量 $(X,Y)$ 是连续型型随机变量，其概率密度为 $f(x,y)$ ，那么 $Z$ 的数学期望等于：

$E(Z)=E(g(X,Y))=\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }g(x,y)f(x,y)dxdy\; \; \; \; \; \; (4)$

备注：假设上式右边的积分绝对收敛。

听海边涛声

关注

5
点赞
踩
11

收藏

觉得还不错? 一键收藏
0
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。