[自动控制原理】实验5利用simulink绘制高阶系统的响应曲线，分析稳态误差

FGO天下第一

已于 2024-11-25 16:52:57 修改

阅读量3.8k

点赞数 8

分类专栏：自动控制原理文章标签：算法 matlab

于 2024-05-29 20:28:03 首次发布

本文链接：https://blog.csdn.net/persona5joker/article/details/139304952

版权

自动控制原理专栏收录该内容

20 篇文章

订阅专栏

实验5基于Simulink控制系统的稳定误差分析

一、实验目的：

1、通过学习本实验内容，学生能够掌握Simulink仿真环境进行控制系统稳态误差分析的方法；

2、研究系统在不同典型输入信号作用下，稳态误差的变化。

二、实验步骤：

1、

四、实验总结：

利用simulink绘制高阶系统的典型输入型号的响应曲线，研究系统在不同典型输入信号作用下，稳态误差的变化。

(1)阶跃输入响应

已知一个单位负反馈系统开环传递函数为G（s）＝K/s(0.1s+1)，分别作出K=5和K=50时，系统单位阶跃响应曲线并求单位阶跃响应稳态误差，总结实验结论。

图 5-1 基于Simulink I型系统单位阶跃响应结构图

1、（1）K=5时I型系统阶跃输入误差响应曲线：

K=50时I型系统阶跃输入误差响应曲线：

结论：稳态误差为零。随着K增大，响应过程变快，但终值不变。

(2)斜坡输入响应

仍然上述系统，分别作出K=0.2 B和K=1时，系统单位斜坡响应曲线并求单位斜坡响应稳态误差，总结实验结论。

图 5-2基于Simulink I型系统单位斜坡响应结构图

（2）K=0.2时I型系统斜坡输入误差响应曲线：

K=1时I型系统斜坡输入误差响应曲线：

结论： K越大，响应越快，稳态误差不变

2、研究系统型次不同，稳态误差的变化。

(1)0型系统在典型输入信号作用下的稳态误差

将上述系统中的积分环节改换为一个惯性环节，开环增益改为1，系统变成0型系统。

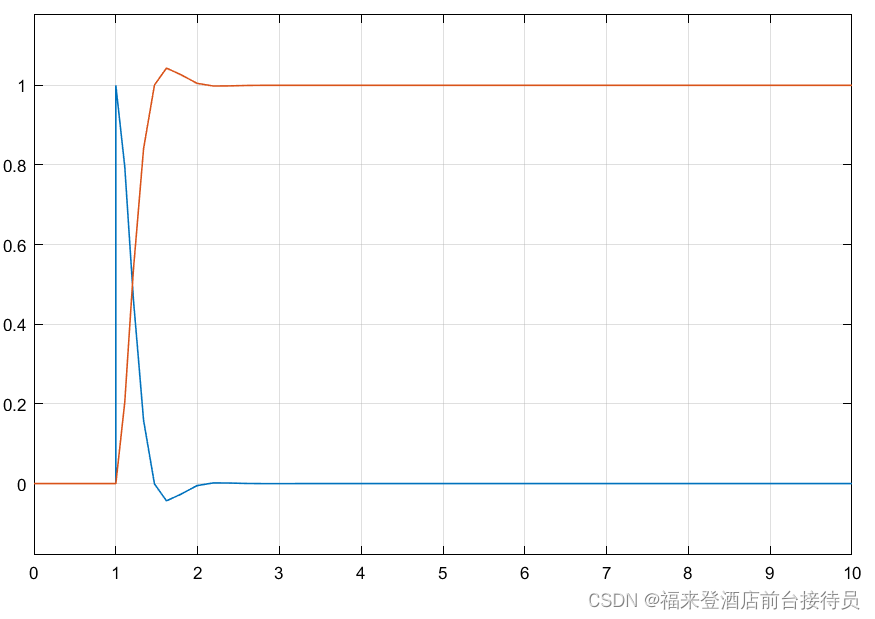
图5-3基于Simulink 0型系统单位阶跃响应误差分析图

在输入端分别给定单位阶跃信号和单位斜坡信号，重新仿真运行，在示波器 Scope 中观察系统响应曲线，并读出稳态误差，总结实验结论。

（1）输入信号为Step的曲线图：

（2）输入信号为Ramp的曲线图：

(2)II型系统在典型输入信号作用下的稳态误差

将上述系统中开环增益改为1，在其前向通道中再增加一个积分环节，系统变成II型系统。在输入端分别给定单位阶跃信号和单位斜坡信号，重新仿真运行，在示波器 Scope 中观察系统响应曲线，并读出稳态误差，总结实验结论。最后，对系统型别、稳态误差和输入信号形式进行归纳，填写表5-1。

图 5-4基于Simulink II型系统单位阶跃和单位斜坡响应误差分析图

（2）输入为Step时的曲线图：

输入为Ramp时的曲线图：

结论：

振荡系统，但最终会趋于稳定

表5-1 输入信号作用下的稳态误差

系统	阶跃输入r(t)=R.1(t)	斜坡输入r(t)=Rt
类别	位置误差e=R/(1+K)	速度误差e=R/K
0	R/1+k	无穷
I	0	R/K
II	0	0

关注作者了解更多

我的其他CSDN专栏

关注作者了解更多

资料来源于网络，如有侵权请联系编者