【自动控制原理】实验6 基于Matlab控制系统的根轨迹及其性能分析 7 系统频率特性及稳定性分析 8 系统频率特性及稳定性分析（上海理工大学）

目录

实验6 基于Matlab控制系统的根轨迹及其性能分析

1、绘制系统的零极点图

3、根据控制系统的根轨迹，分析控制系统的性能。

实验 7 系统频率特性及稳定性分析

1、绘制控制系统 Nyquist 图

2、根据 Nyquist 图分析系统稳定性

实验8 系统频率特性及稳定性分析

2、校正设计案例二

---

实验6 基于Matlab控制系统的根轨迹及其性能分析

一、实验目的：

1、通过学习本实验内容，学生能够掌握使用 MATLAB绘制控制系统零极点图和根轨迹图的方法；

2、学会分析控制系统根轨迹的一般规律；

3、能够利用根轨迹图进行系统性能的分析；

4、研究闭环零极点对系统性能的影响。

二、实验步骤：

1、绘制系统的零极点图

（1）已知系统的开环传递函数G(s)H(s)=(s^2+5s+5)/s(s+1)(s^2+2s+2)绘制系统的零极点图，读取数据填入表6-1中，总结规律。

matlab代码：

num=[1 5 5];den=[1 ,3 ,4, 2 ,0];sys=tf(num,den);figure;pzmap(sys)

根轨迹曲线

表6-1 系统零极点图

零极点	阻尼比ζ	超调量Mp	振荡频率wn
零点1=-1.38	1	0	1.38
零点2=-3.62	1	0	3.62
极点1=-1	1	0	1
极点2=0	-1	0	0
极点3=-1+i	0.707	4.32	1.41
极点4=-1-i	0.707	4.32	1.41

（2）若已知系统开环传递函数G(s)H(s)= k/s(s+1)(s+2),绘制控制系统的根轨迹图，并完成填空：

matlab代码：

clear all; close all;num=[1];den=[1 3 2 0];sys=tf(num,den);rlocus(sys)

根轨迹曲线：

填空

(1) 根轨迹有__ 3__条。

(2) 位于负实轴上的根轨迹(-∞，2)和(1，0)区段，其对应的阻尼ζ_____ 1_____，超调量为__ 0____，系统处于_ 临界阻尼 __状态，而且在远离虚轴的方向，随着增益K增大，振荡频率ω__ 增加___，系统动态相应衰减速率___增加 _____。

(3) 在根轨迹的分离点为___-0.423 ____，对应于阻尼ζ___1 ____，超调量为_0_ __，开环增益K=__ __，系统处于____ 临界阻尼_____状态。

(4) 根轨迹经过分离点后离开实轴，朝5右半平面运动。当根轨迹在分离点与虚轴这个区间时，闭环极点由___ -0.423____变为____0 ____，对应阻尼0<ζ<1，系统处于__ _欠阻尼___状态，其动态响应将出现__减幅_ ___振荡，而且越靠近虚轴，增益K越大，阻尼越小，超调量_ 增加 _，振荡频率ω__增加 __。

(5) 当根轨迹与虚轴相交时，闭环根位于虚轴上，闭环极点是一对纯虚根__+1.41i,-1.41i_ ____，阻尼___0 ___，超调量达到__100% ____，系统处于___ 临界阻尼___状态，其动态响应将出现__ 等幅____振荡。此时称为临界稳定增益K2=_ __6___。

3、根据控制系统的根轨迹，分析控制系统的性能。

已知一负反馈系统的开环传递函数为G(s)H(s)= k(s+3)/s(s+2)

(1) 绘制其根轨迹图，确定根轨迹的分离点与相应的增益。

使用代码:

clear all; close all;num=[1 3];den=[1 2 0];sys=tf(num,den);rlocus(sys)

得到根轨迹图：

(2) 确定系统呈现欠阻尼状态时的开环增益范围。
0.536<k<7.46

(3) 确定系统最小阻尼比时的闭环极点。

Z=0时的阻尼比最小

加深了我对系统根轨迹图绘制法则的了解，了解系统阻尼比等概念。

实验 7 系统频率特性及稳定性分析

一、实验目的：

1、通过学习本实验内容，学生能够掌握频率特性的测量方法；

2、能够分析控制系统 Nyquist 图的基本规律；

3、掌握使用 MATLAB 绘制控制系统 Bode 图和分析稳定性的方法

二、实验步骤：

1、绘制控制系统 Nyquist 图

已知 G(s)H(s)=0.5/(s^3+2s^2+s+0.5), 计算系统特征根,并绘制 Nyquist 图,判定系统的稳定

性.

matlab使用代码：

num=[0.5];den=[1 2 1 0.5];

G=tf(num,den);pole(G)

nyquist(G)

得到结果及奈氏图如下：

ans =

-1.5652 + 0.0000i

-0.2174 + 0.5217i

-0.2174 - 0.5217i

论：系统不具有正实部的根，且奈氏图越过（-1,0）的次数为 0，系统稳定。

2、根据 Nyquist 图分析系统稳定性

(1)已知系统开环传递函数为 G(S)=K(T1s+1)/s^2(T2s+1), 分别作出 T1>T2 和 T1<T2 时的 Nyqusit

图, 判定系统的稳定性,比较两图的区别与特点。(T1 和 T2 可以自拟参数)

解：T1>T2 时，

使用代码: num=[20 10];num=[1 1 0 0];G=tf(num,den);figure();nyquist(G);grid on

结论：系统逆时针包围临界点圈数等于开环正实部极点数，系统稳定

当T1<T2 时，

使用代码：

num=[1 1];num=[6 1 0 0];G=tf(num,den);figure();nyquist(G);grid on

结论： 系统正穿越临界点的圈数不等于开环正实部极点数，系统不稳定

---

(2)已知系统开环传递函数为 G(S)H(s)=K/s^v(s+1)(s+2) (v 和 K 可以自拟参数)

令 v=1,

使用代码:

num=[1 ];num=[1 3 2 0];G=tf(num,den);figure();nyquist(G);grid on

结果截图为:

结论: 当 k 小于临界值时，系统稳定，当 k 大于临界值时，系统不稳定。

令 k=1,

使用代码:

num=[1 ];num=[1 3 2 0];G=tf(num,den);figure();nyquist(G);grid on

结论: 当 v=1 时，系统稳定，当 v 大于 1 时，系统不稳定。

3、绘制控制系统 Bode 图

(1)已知控制系统开环传递函数 G(s)H(s)=10/( s2+2s+10)绘制其 Bode 图,判定系统的稳定性。

使用代码：

num=[10 ];num=[1 2 10 ];G=tf(num,den);figure();bode(G);grid on

结果截图：

结论： 裕度为正，系统稳定

(2)已知单位负反馈系统的开环传递函数为 G(s)=2/s(s+1)(s+2)绘制其 Bode 图,求系统的稳定裕

度。

使用代码:

num=[2 ];num=[1 3 2 0 ];G=tf(num,den);figure();bode(G);grid on

结果截图:

结论：裕度为正，系统稳定

4、根据 Bode 分析系统稳定性

(1)系统开环传递函数 G(s)= K/s(0.5s+1)(.1s+1)，尝试 k 取不同的值时,分析系统的稳定性,找

出系统的临界稳定时的增益 K。

使用代码: num=[1 ];num=[0.5 1.5 1 ];G=tf(num,den);figure();bode(G);grid on

结果截图:

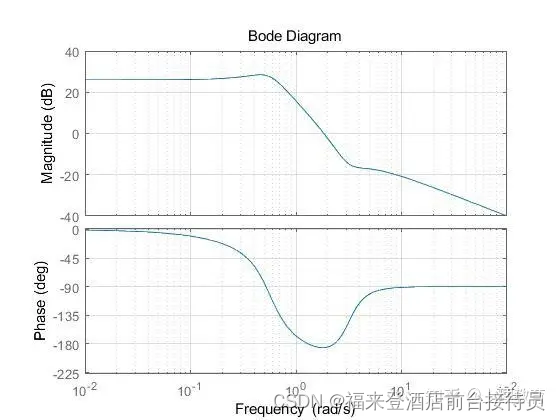
(2)已知系统开环传递函数 G(s)= k(s+1)/ s^2(0.1s+1),令 K=1 作 Bode 图,应用频域稳定判据确

定系统的稳定性,并确定使系统获得最大相位裕度 y 的增益 K 值。

使用代码:

num=[1 1];num=[0.1 1 0 0 ];G=tf(num,den);figure();bode(G);grid on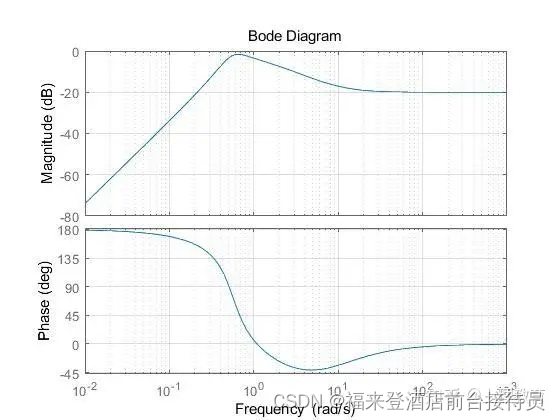

让我学会正确运用奈氏图和 BODE 图判定系统稳定性

实验8 系统频率特性及稳定性分析

一、实验目的：

1、通过学习本实验内容，学生能够掌校正设计方法；

2、巩固掌握使用 MATLAB 绘制控制系统 Bode图和分析稳定性的方法。

二、实验步骤：

1、校正设计案例一

已知系统开环传递函数G()=1/s^2(s+10)

试用根轨迹编辑器对系统进行补偿设计,使系统单位阶跃给定响应一次超调后就衰减;并在根轨迹编辑器中观察根轨迹图,以及系统阶跃响应曲线

步骤:

(1)调用rltool {()函数,打开带系统的根轨迹编辑器;

---

(1) 输入代码：

>> num=[1];den=[1 10 0 0 ];G=tf(num,den);rltool(G)

结果截图：

结论：发散

(2)确定控制系统的结构,选择其中的控制器模块(s)进行参数配置;

(2) 选中模块C进行参数配置

改变增益，扔发散

结论：有变化，在无穷处仍发散震荡

(3)在补偿器编辑窗口可动态调整增益大小附加零点或极点关键步骤

(3) 添加一个零点z=-10，

结论：添加零点，发散震荡，在无穷处衰减

(4)在根轨迹编辑器窗口中系统观察根轨迹

(5)在根轨迹编辑器窗口中系统观察阶跃响应曲线,读取动态性能指标;

(6)重复进行步骤(3)~(5),可以设计出符合题意要求的系统。多次尝试,可以掌握补偿增益和附加实数(或复数)零极点之间匹配的规律。

由此减小零点的绝对值大小z=-1，并将增益增大(K=30);

截图：

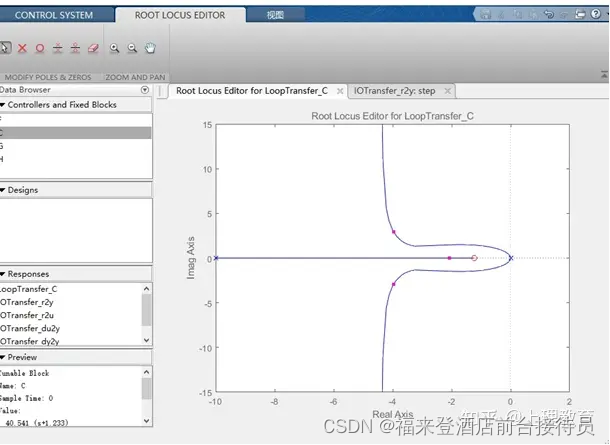
函数阶跃超调一次后就衰减

结论

通过添加零点z=-1，改变增益，可以进行系统校正，设计出符合题意的系统。

2、校正设计案例二

已知系统开环传递函数G(s)=10/(0.5s^2+s)

要求用根轨迹法设计超前校正装置Gc,要K>20,希望该单位负反馈系统的时域性能指标M<15%,1.5

输入代码：num=[10];den=[0.5 1 0 ];G=tf(num,den);rltool(G)

得到结果截图:

我们可以看到系统已经可以达到稳定状态，但是超调量48.5不满足题设要求，于是配置参数K=21，并新增一个零点z=-1；此时系统为过阻尼状态。

截图：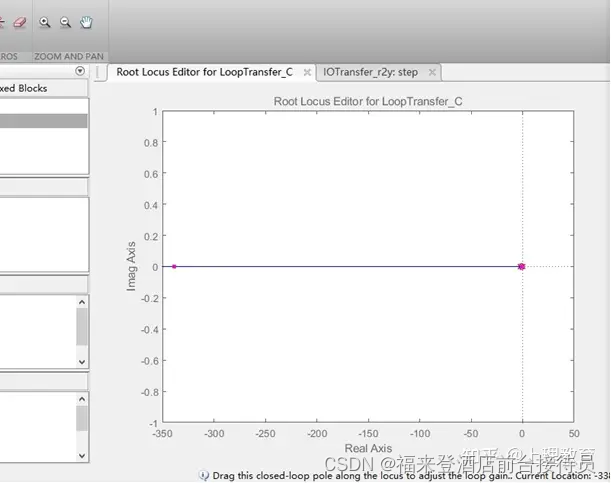

我们 因此将z值缩小10倍，即z=-10，得到结果：

增加零点和改变系数可以调节系统阻尼，调节系统稳定性

让我知道了增益系数k和添加零点对系统稳定性的影响

---

资料仅供学习使用

编者能力有限，如有错误欢迎留言交流

编者的其他专栏：

C语言

单片机原理

模式识别原理

数字电子技术

自动控制原理

模拟电子技术

数据结构

线性代数

复变函数与积分变换

 概率论与数理统计

高等数学

大学物理

电路原理

关注编者了解更多