0. 受控对象与设计要求
这里列出上一篇文章的结果
0.1 受控对象
P
p
e
n
d
(
s
)
=
Φ
(
s
)
U
(
s
)
=
m
l
q
s
s
3
+
b
(
I
+
m
l
2
)
q
s
2
−
(
M
+
m
)
m
g
l
q
s
−
b
m
g
l
q
[
r
a
d
N
]
P_{pend}(s) = \frac{\Phi(s)}{U(s)}=\frac{\frac{ml}{q}s}{s^3+\frac{b(I+ml^2)}{q}s^2-\frac{(M+m)mgl}{q}s-\frac{bmgl}{q}} \qquad [ \frac{rad}{N}]
Ppend(s)=U(s)Φ(s)=s3+qb(I+ml2)s2−q(M+m)mgls−qbmglqmls[Nrad]
P
c
a
r
t
(
s
)
=
X
(
s
)
U
(
s
)
=
(
I
+
m
l
2
)
s
2
−
g
m
l
q
s
4
+
b
(
I
+
m
l
2
)
q
s
3
−
(
M
+
m
)
m
g
l
q
s
2
−
b
m
g
l
q
s
[
m
N
]
P_{cart}(s) = \frac{X(s)}{U(s)} = \frac{ \frac{ (I+ml^2)s^2 - gml } {q} }{s^4+\frac{b(I+ml^2)}{q}s^3-\frac{(M+m)mgl}{q}s^2-\frac{bmgl}{q}s} \qquad [ \frac{m}{N}]
Pcart(s)=U(s)X(s)=s4+qb(I+ml2)s3−q(M+m)mgls2−qbmglsq(I+ml2)s2−gml[Nm]
其中:
q
=
[
(
M
+
m
)
(
I
+
m
l
2
)
−
(
m
l
)
2
]
q=[(M+m)(I+ml^2)-(ml)^2]
q=[(M+m)(I+ml2)−(ml)2]
0.2 设计要求
对于倒立摆,当小车受到1Nsec的冲激响应的时候:
- θ的稳定时间 < 5s
- |θ-θ0| < 0.05 radians
对于整个系统,当小车收到0.2m的阶跃信号的时候:
- x 与 θ 的稳定时间 < 5s
- x 的上升时间 < 0.5s
- |θ-θ0| < 0.05 radians (也就是20°)
- 对于x和θ来说,稳态误差 < 2%
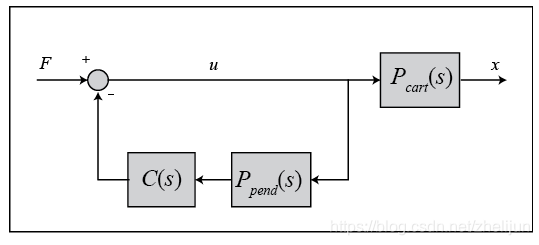
0.3 系统结构
由上一节我们知道该系统的控制结构框图:

该系统的转换方程为:
T
(
s
)
=
Φ
(
s
)
F
(
s
)
=
P
p
e
n
d
(
s
)
1
+
C
(
s
)
P
p
e
n
d
(
s
)
T(s) = \frac{\Phi(s)}{F(s)} = \frac{P_{pend}(s)}{1 + C(s)P_{pend}(s)}
T(s)=F(s)Φ(s)=1+C(s)Ppend(s)Ppend(s)
在开始设计PID控制器之前,我们先在Matlab里面定义好我们的受控对象
M = 0.5;
m = 0.2;
b = 0.1;
I = 0.006;
g = 9.8;
l = 0.3;
q = (M+m)*(I+m*l^2)-(m*l)^2;
s = tf('s');
P_pend = (m*l*s/q)/(s^3 + (b*(I + m*l^2))*s^2/q - ((M + m)*m*g*l)*s/q - b*m*g*l/q);
1. 根轨迹设计
本节我们用根轨迹法来为该不稳定系统设计一个控制器。通过下面的代码显示当一个比例控制系数K从0到无穷大时的闭环根轨迹
rlocus(P_pend)
title('Root Locus of Plant (under Proportional Control)')
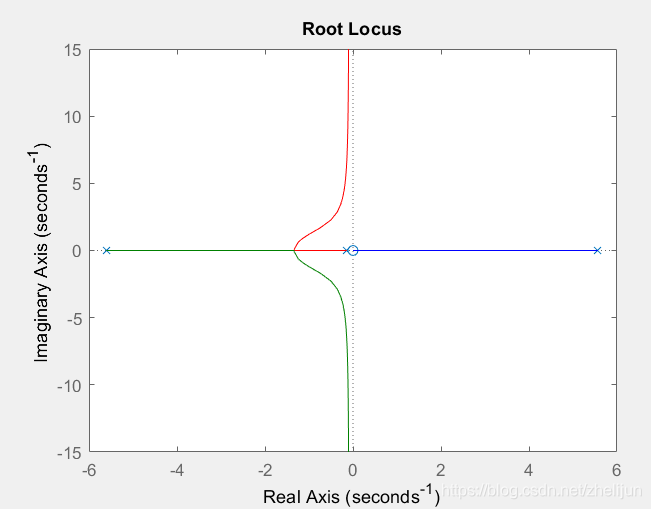
不难发现有一段轨迹线无论K怎么变化,始终都在s平面右半边。也就是说无论K怎么变化,该系统始终不稳定。
为了解决这个问题,我们需要在原点处添加一个极点来抵消原点零点的影响,然后再通过添加修改控制器把s平面右边的极点统统拉到左平面以稳定整个系统。
C = 1/s;
rlocus(C*P_pend)
title('Root Locus with Integral Control')
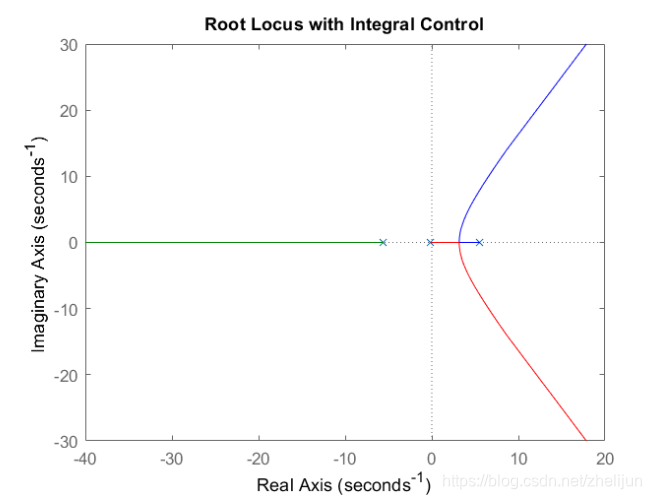
我们看一下零极点
zeros = zero(C*P_pend)
poles = pole(C*P_pend)
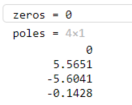
新的系统有一个零点和四个极点,刨去相同位置下的零极点,那么根轨迹相应的有三条。新的根轨迹同样有一段永远在虚轴右边,一般来说我们通过增加零点把根轨迹往虚轴左边拉。由根轨迹的知识可知根轨迹与s平面实轴的交点在:
s
=
Σ
p
o
l
e
s
−
Σ
z
e
r
o
s
#
p
o
l
e
s
−
#
z
e
r
o
s
s = \frac{\Sigma poles - \Sigma zeros}{\#poles - \#zeros}
s=#poles−#zerosΣpoles−Σzeros
因此如果我们添加一个最小相位零点的话(负零点),系统 与虚轴的交点为:
s
=
(
−
5.6041
+
5.5651
−
0.1428
+
0
)
−
(
0
−
z
)
4
−
2
=
−
0.1818
+
z
2
s = \frac{(-5.6041+5.5651-0.1428+0)-(0-z)}{4-2} = \frac{-0.1818+z}{2}
s=4−2(−5.6041+5.5651−0.1428+0)−(0−z)=2−0.1818+z
因此最远我们大概可以把轨迹拖到-0.1的位置(这个结论是怎么得到的),回忆我们估计2%稳定时间的公式:
T
s
=
4
σ
T_s = \frac{4}{\sigma}
Ts=σ4
因此,上述操作并不能使系统5秒的稳定时间满足条件。
2. PID控制
上述分析后我们知道给我们的微分控制器添加零点可以把根轨迹拖到s平面左边,但是拖得又不够左边。一种可行的方法是添加多一个零点。如果我们把两个零点放在负实轴极点中间,那么根轨迹会收敛于这两个极点。假设我们添加了-3 和 -4 两个零点
z = [-3 -4];
p = 0;
k = 1;
C = zpk(z,p,k);
rlocus(C*P_pend)
title('Root Locus with PID Controller')
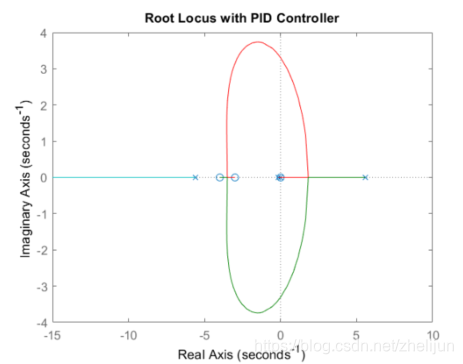
现在我们来看看新的系统是否满足设计要求。要求1,我们希望稳定时间<5秒,因此主极点的实部需要在4/(-5)= - 0.8 的左边才行,我们的主极点明显满足要求。要求2,我们希望超调不超过0.05弧度,因此就要求我们的系统有足够的阻尼,把主极点放在靠近实轴的地方会增大阻尼系数。我们运行以下代码来定位一个K,并输出响应K值下面新系统的零极点。
[k,poles] = rlocfind(C*P_pend)
Matlab会弹出一个窗口然你选择根轨迹的位置,然后帮你输出对应根轨迹下的K值以及相应的零极点。我们在接近实轴的地方大概找了一个点
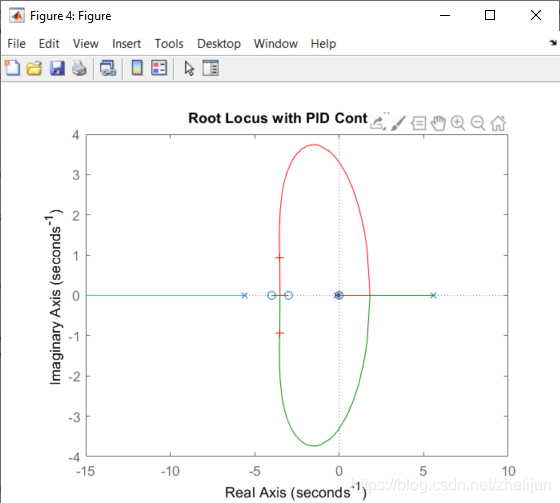
然后matlab输出(不同人点的位置极有可能不一样,所以差不多就好)
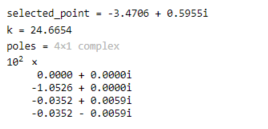
如此这般,我们就得到了一个新系统,我们再看看该系统是否满足超调性能
K = 24.6;
T = feedback(P_pend,K*C);
impulse(T)
title('Impulse Disturbance Response of Pendulum Angle under PID Control');
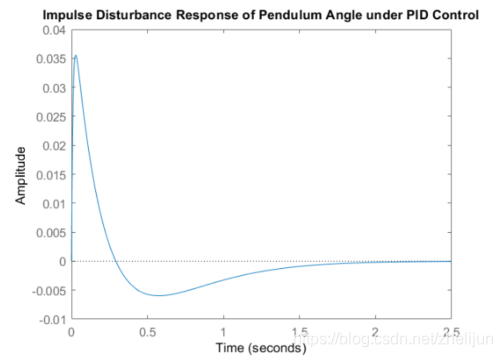
通过仿真,第二个设计要求也满足了!
3. 那小车呢?
就跟上一节我们讲到的那样,该系统是单输入二输出系统,其系统框图为
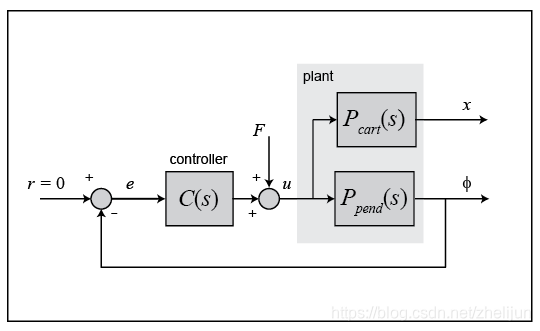
整理一下
于是上面我们设计好了控制器之后,我们的输入对于小车的输出转换方程为
T
2
(
s
)
=
X
(
s
)
F
(
s
)
=
P
c
a
r
t
(
s
)
1
+
P
p
e
n
d
(
s
)
C
(
s
)
T_2(s) = \frac{X(s)}{F(s)} = \frac{P_{cart}(s)}{1 + P_{pend}(s)C(s)}
T2(s)=F(s)X(s)=1+Ppend(s)C(s)Pcart(s)
由之前对小车倒立摆模型的分析可知
P
c
a
r
t
(
s
)
=
X
(
s
)
U
(
s
)
=
(
I
+
m
l
2
)
s
2
−
g
m
l
q
s
4
+
b
(
I
+
m
l
2
)
q
s
3
−
(
M
+
m
)
m
g
l
q
s
2
−
b
m
g
l
q
s
[
m
N
]
P_{cart}(s) = \frac{X(s)}{U(s)} = \frac{ \frac{ (I+ml^2)s^2 - gml } {q} }{s^4+\frac{b(I+ml^2)}{q}s^3-\frac{(M+m)mgl}{q}s^2-\frac{bmgl}{q}s} \qquad [ \frac{m}{N}]
Pcart(s)=U(s)X(s)=s4+qb(I+ml2)s3−q(M+m)mgls2−qbmglsq(I+ml2)s2−gml[Nm]
其中:
q
=
[
(
M
+
m
)
(
I
+
m
l
2
)
−
(
m
l
)
2
]
q=[(M+m)(I+ml^2)-(ml)^2]
q=[(M+m)(I+ml2)−(ml)2]
我们把设计好的控制器和小车的转换方程代入进
T
2
(
s
)
T_2(s)
T2(s) 里,并查看阶跃输出
P_cart = (((I+m*l^2)/q)*s^2 - (m*g*l/q))/(s^4 + (b*(I + m*l^2))*s^3/q - ((M + m)*m*g*l)*s^2/q - b*m*g*l*s/q);
T2 = feedback(1,P_pend*C)*P_cart;
t = 0:0.01:8.5;
impulse(T2, t);
title('Impulse Disturbance Response of Cart Position under PID Control');
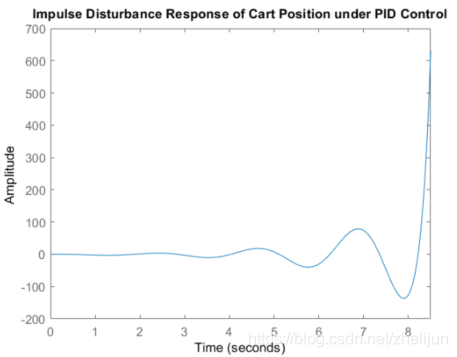
可以发现为了保持倒立摆的稳定,小车的运动是发散的。因此,显然我们不能用SISO的设计方法去处理SIMO的系统。
4. 几个问题
- 为什么要加原点极点?
- 为啥添加的最小相位零点取值接近0?
- 2% 稳定时间公式的依据在哪里?
- 主极点放在实轴附近增大阻尼系数的依据来源于哪里?
5. 引用
https://ctms.engin.umich.edu/CTMS/index.php?example=InvertedPendulum§ion=ControlRootLocus






















 1361
1361











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








