关注作者了解更多
我的其他CSDN专栏
关注作者了解更多
资料来源于网络,如有侵权请联系编者
目录

8.1 图像退化机理
什么是图像的退化
图像退化原因
图像退化的处理方法
什么是图像复原
图像增强和图像复原的区别
1.什么是图像退化?
在景物成像过程中,由于目标的高速运动、散射、成像系统畸变和噪声干扰,致使最后形成的图像存在种种恶化,称之为“退化”。
退化的形式有图像模糊或图像有干扰等。


2. 图像退化原因
成像系统镜头聚焦不准产生的散焦;
相机与景物之间的相对运动;
成像系统存在的各种非线性因素以及系统本身的性能 ;
射线辐射、大气湍流等因素造成的照片畸变;
成像系统的像差、畸变、有限带宽等;
底片感光图像显示时会造成记录显示失真;
成像系统中存在的各种随机噪声 ;
3.图像退化的处理方法
无论是由光学、光电或电子方法获得的图像都会有不同程度的退化;退化的形式多种多样,如传感器噪声、摄像机未聚焦、物体与摄像设备之间的相对移动、光学系统的相差、成像光源或射线的散射等;
如果我们对退化的类型、机制和过程都十分清楚,那么就可以利用其反过程来复原图像。

4. 什么是图像复原?
图像复原是通过对图像退化的过程进行估计,并补偿退化过程造成的失真,以便获得未经干扰退化的原始图像或原始图像的最优估值,从而改善图像质量的一种方法。
图像复原是图像退化的逆过程。
典型的图像复原方法:根据图像退化的先验知识建立退化模型,以此模型为基础,用滤波等手段进行处理,使复原图像符合一定的准则,达到复原图像的目的。




5. 图像增强和图像复原的区别?
图像增强是为了突出图像中感兴趣的特征,增强后的图像可能与原始图像存在一定的差异。 评判图像增强质量好坏的是主观标准。
图像复原是针对图像退化的原因做出补偿,使恢复后的图像尽可能接近原始图像。 评判图像复原质量好坏的是客观标准。
8.2 图像退化模型
1)线性特性
2)位置不变性

H(x,y)概括了图像退化的物理过程




连续退化模型几点说明:
(1)若线性成像系统的冲击响应是理想的,即Hδ(x-α,y-β)=δ(x-α,y-β),那么形成的图像g(x,y)就和原始图像一样,不产生模糊。

(2) 若冲激响应是非理想的,则造成图像模糊。 通常把成像系统考虑成为线性位移不变系统,即



(3)退化的另一种现象,噪声污染,假定噪声是加性的,那么退化模型为

傅氏变换

数字图像讨论的是离散的图像函数,因此需要对连续模型进行离散化处理,即将连续模型中的积分以求和的形式表示。
1. 一维退化模型
对f(x)及h(x)均匀采样,样本数分别为A及B,即:
f(x) x=0,1,…,A-1
h(x) x=0,1,…,B-1
离散循环卷积是针对周期函数定义的
如果f(x)及h(x)都是具有周期为N的序列,那么离散的退化模型可表示为:

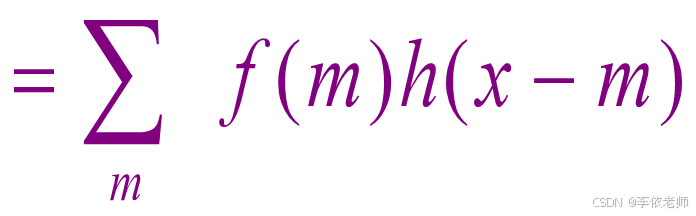
为了不使离散循环卷积时发生相互重叠现象,必须对f (x)和h (x)进行周期延拓.

则fe(x)和he(x)可分别表示为:

f e (x)、 he(x)均是长度为M的周期序列,其卷积为

g e (x)也是长度为M的周期序列。
若把f e (x)、 g e (x) 表示成向量形式:

循环卷积写成矩阵形式:
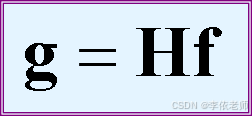
H是M*M的矩阵。

利用周期特性:he(x)=he(x+M)可得

循环矩阵:方阵,下一行是上一行循环右移一位的结果.
2. 二维离散退化模型
f (x,y)、h (x,y)均匀采样,样本数分别为A*B,C*D。周期性地延拓成M*N样本

则循环卷积为

矩阵形式 :

H是分块循环矩阵。

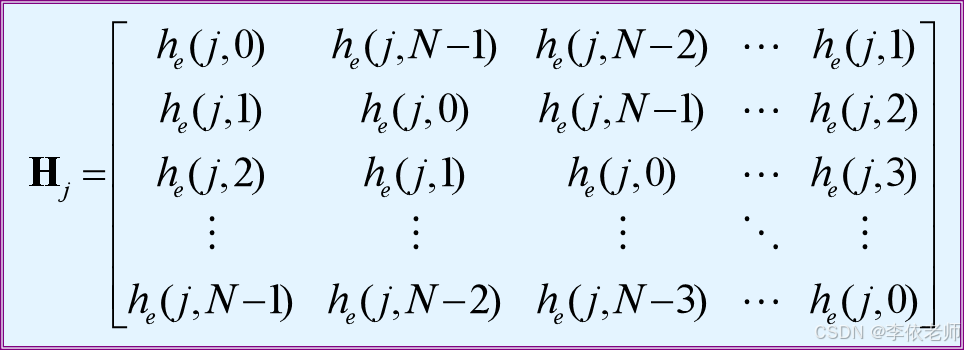
若n是MN 维噪声,则退化模型为:


3.退化参数的确定
退化参数:
h(x,y) n(x,y)
图像恢复:
对原始图像作出尽可能好的估计。 已知退化图像,要作这种估计,须知道退化参数的有关知识。
4.点扩展函数的确定
1) 运用先验知识:
大气湍流
光学系统散焦
照相机与景物相对运动
根据模糊的物理过程(先验知识)来确定h(x,y)或H(u,v)。
(1)长时间曝光下大气湍流造成的转移函数

C是与湍流性质有关的常数。
(2)光学散焦

d是散焦点扩展函数的直径; J1(•)是第一类贝塞尔函数。
(3)照相机与景物相对运动 设T为快门时间,x0(t),y0(t)是位移的x分量和y分量

5. 噪声的确定
需知道n(x,y)的统计性质,以及n(x,y)与f(x,y)之间的相关性质。
一般假设图像中的噪声是一类白噪声。
白噪声:图像平面上不同点的噪声是不相关的,其谱密度为常数。
当噪声与图像不相关时,噪声是加性的。 在有些情况下噪声大小确实与图像信号有关。如以下的乘性白噪声

8.3 无约束复原
无约束复原方法
逆滤波复原
有约束复原(最小二乘类复原)
图像复原的主要目的是当给定退化的 图像g(x,y)及系统h(x,y)和噪声n(x,y)的 某种了解或假设,估计出原始图像f(x,y)。 其代数表达式即:
g=Hf+n
因此,可用线性代数中的理论解决复原 问题。
复原时以消除噪声为目的,可将上式改为:\

在最小二乘方意义上说,希望找到一个 使
 为最小。
为最小。





这种方法要求知道成像系统的点扩散函数H.




8.4 逆滤波复原方法
逆滤波复原基本原理
\

逆滤波复原举例


复原图像频谱





(1)逆滤波的应用条件是退化图像g(x,y)是信噪比较高的图像。
(2)如果H (u ,v)有许多零点,必然使得复原的结果受到极大影响。
(3)如果H (u ,v)不为零但是有非常小的值,也即病态条件,也会使复原效果受到影响。
8.5 有约束复原
最小二乘类约束复原
性能指标J (f )如下:



令γ=1/λ


维纳滤波原理是使 和 的均方误差最小实现的滤波方法
维纳滤波法
维纳滤波的基本原理是将原始图像f和对原始图像 的 估计看作为随机变量,按照使f和估计值 之间的均方 误差达到最小的准则实现图像复原。
均方误差如下:

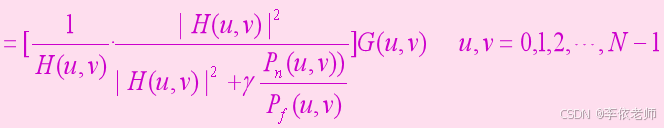
若γ=1,则称为维纳滤波器
本章主要知识点
什么是图像的退化
图像的退化及复原模型
无约束复原基本原理
逆滤波方法基本原理
几种有约束复原基本原理
匀速直线运动模糊复原
几何畸变的三角形校正

























 5539
5539

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










