MIMO-OFDM无线通信技术及MATLAB实现（2）SISO信道模型

1candobetter

已于 2022-05-11 10:18:50 修改

阅读量5.1k

点赞数 4

分类专栏：通信书籍读书笔记文章标签： matlab 算法开发语言

于 2022-05-04 15:44:02 首次发布

本文链接：https://blog.csdn.net/pgone1/article/details/124561975

版权

通信书籍读书笔记专栏收录该内容

7 篇文章

订阅专栏

信道模型能够随着接收机和发射机天线配置的改变而改变，即取决于单天线系统和多天线系统。特别的在MIMO系统的研究过程中，需要一个完全不同的信道模型来捕获其空-时特点（即多接收天线和多发射天线中不同路径之间的相关性）

室内信道模型

当信号强度在一个符号周期内随时间的波动程度较小时，可认为信道环境是静态的。这种特殊情况被称为准静态信道环境。对室内信道进行建模时，通常假设信道为静态或准静态的。

一般室内信道模型

2-径模型（两条射线，一条是零时延的直射路径，一条是时延大于0的反射路径，两条路径的功率相同，第二条路径的时延是决定这一特殊模型的唯一参数）
指数模型（信道的平均功率随着信道的时延按指数规律递减）

IEEE 802.11信道模型

IEEE 802.11b任务组采纳了指数模型来代表2.4GHz的室内信道。它的功率时延服从指数模型。可以用有限脉冲响应（FIR）滤波器的输出表示信道脉冲响应。将每个信道抽头建模为独立的复高斯随机变量，其功率服从指数的PDP，每一抽头的时间编号取样为采样周期的整数倍。最大的路径数由RMS时延扩展和采样值周期数决定: $gif.latex?P_{max}=[rac{10*sigma _{_{ au }}}{T{s}}]$ , $gif.latex?sigma _{ au }$ 为时延扩展, $gif.latex?T_{s}$ 为采样周期

Saleh-Valenzuela信道模型

通过对室内信道的大量测量，可以将多径时延分量的到达过程建模为泊松过程。在时延分布中存在多簇现象，而且每一簇中又有多条射线。S-V信道模型，其中每一簇对应一组射线。每一簇以及每一簇内射线的到达时间是泊松过程。簇间到达时间分布和簇内射线间道道时间的分布服从指数分布。 每次实现的路径数也就是子径数。

UWB信道模型

根据对室内带宽信道的测量，我们发现尽管多径衰落幅度也显示出和S-V信道模型一样的簇现象，但这些幅度服从对数正态分布或Nakagami分布，而不是瑞利分布。基于这个结论，通过修改S-V模型，使多簇信号和每簇内的多径信号都服从独立的对数正态衰落。

室外信道模型

室外信道受终端移动速度的影响，其典型特点使信道增益随时间的变化而变化。信道增益的时变性依赖于移动台的速度，并且受多普勒谱的影响。多普勒谱决定了信道增益的时域相关性。

FWGN信道模型

室外信道的特点主要由控制信道增益随时间变化的多普勒谱来描述。可以通过滤波后的高斯白噪声（FWGN）模型实现不同类型的多普勒谱。Clarke/Gans模型是一种基本的FWGN模型，根据如何在时域或频域实现多普勒滤波器，可以将Clarke/Gans修改成其他各种类型。

Clarke/Gans模型

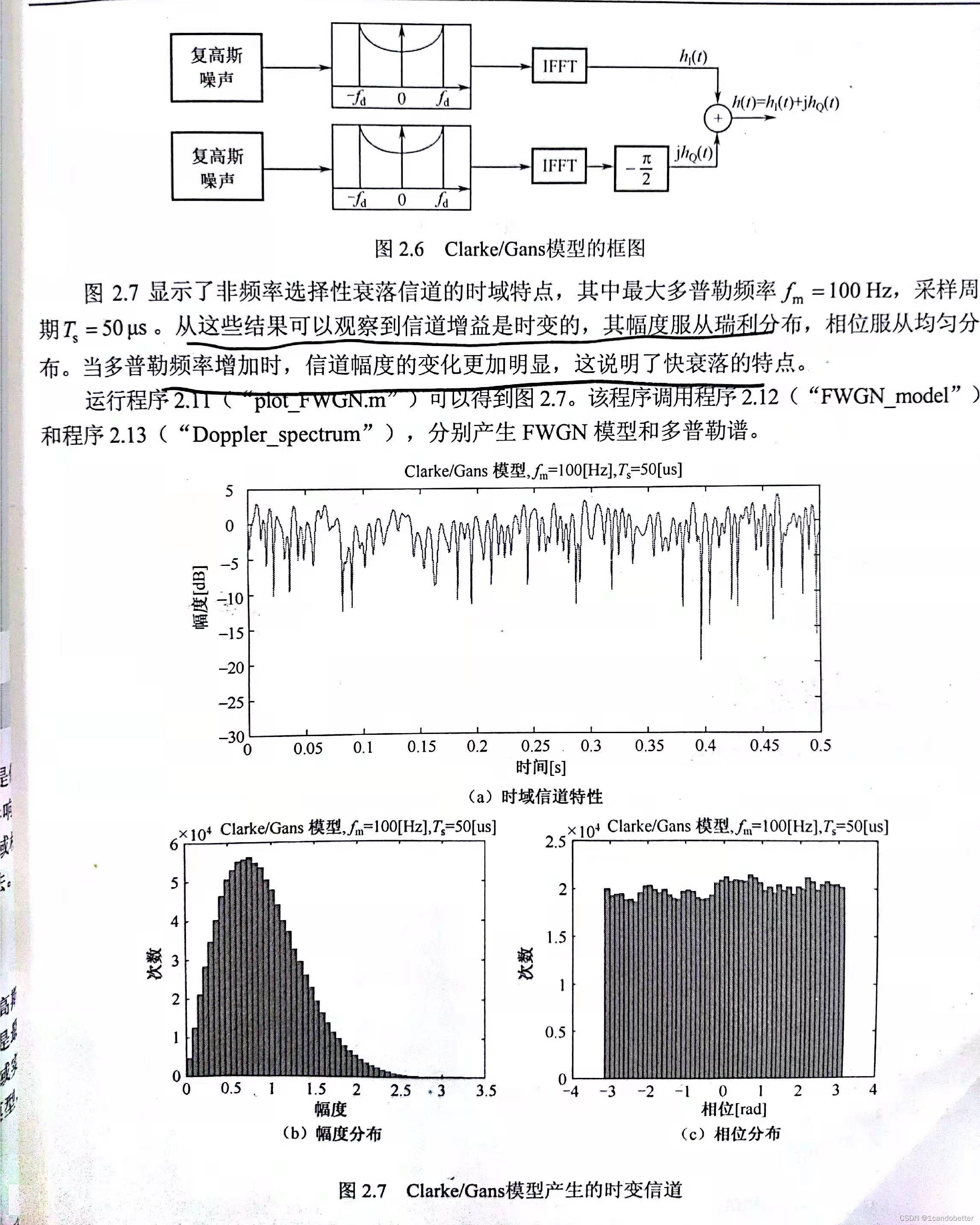
假设条件：移动台周围的散射分量是均匀分布的，且每一分量的功率都相等。图中有两个分支。

在频域产生一个复高斯噪声
通过一个多普勒滤波器（频域分量符合多普勒频移）
将这个经过多普勒频移的高斯噪声通过IFFT模块变成时域信号（由于IFFT的输出必须是实信号，所以IFFT模块的输入必须是共轭对称的）
将输出的实部和虚部加起来可以构建一个复信道增益，从而产生幅度服从瑞利分布的信道

根据信道检测的报告可知，不同的信道环境有不同的多普勒谱，而且每条路径的最大多普勒频率和多普勒谱可能会发生变化。

在频域模型中，衰落信道的持续时间由IFFT的大小和频域过采样系数共同决定

在时域模型中，衰落信道的持续时间由复高斯随机信号的长度决定

在使用FIR滤波器实现多普勒滤波的情况下，其计算复杂度随着抽头数量的增加而呈指数增长。

Jakes模型

通过对复正弦波的合成，可以产生服从给定多普勒谱的瑞利衰落信道。为了使产生的信号幅度近似瑞利分布，正弦波的数量必须足够大。此外，必须对每个正弦波发生器进行加权，以产生想要的多普勒谱。这就是Jakes模型。

基于射线的信道模型

基于射线的模型能够考虑空、时相关性，所以经常被用于MIMO信道的建模。然而，它同样适用于SISO信道。和Jakes模型一样，基于射线的模型由道道平面波的总和给出。基于射线的模型能在各种散射环境下模拟移动台周围以认以方向到达的平面波，且通常不是均匀的功率方位谱（PAS）与Jakes不同，它的多普勒谱不是U形谱，而是根据散射环境的不同而呈不同的形式。

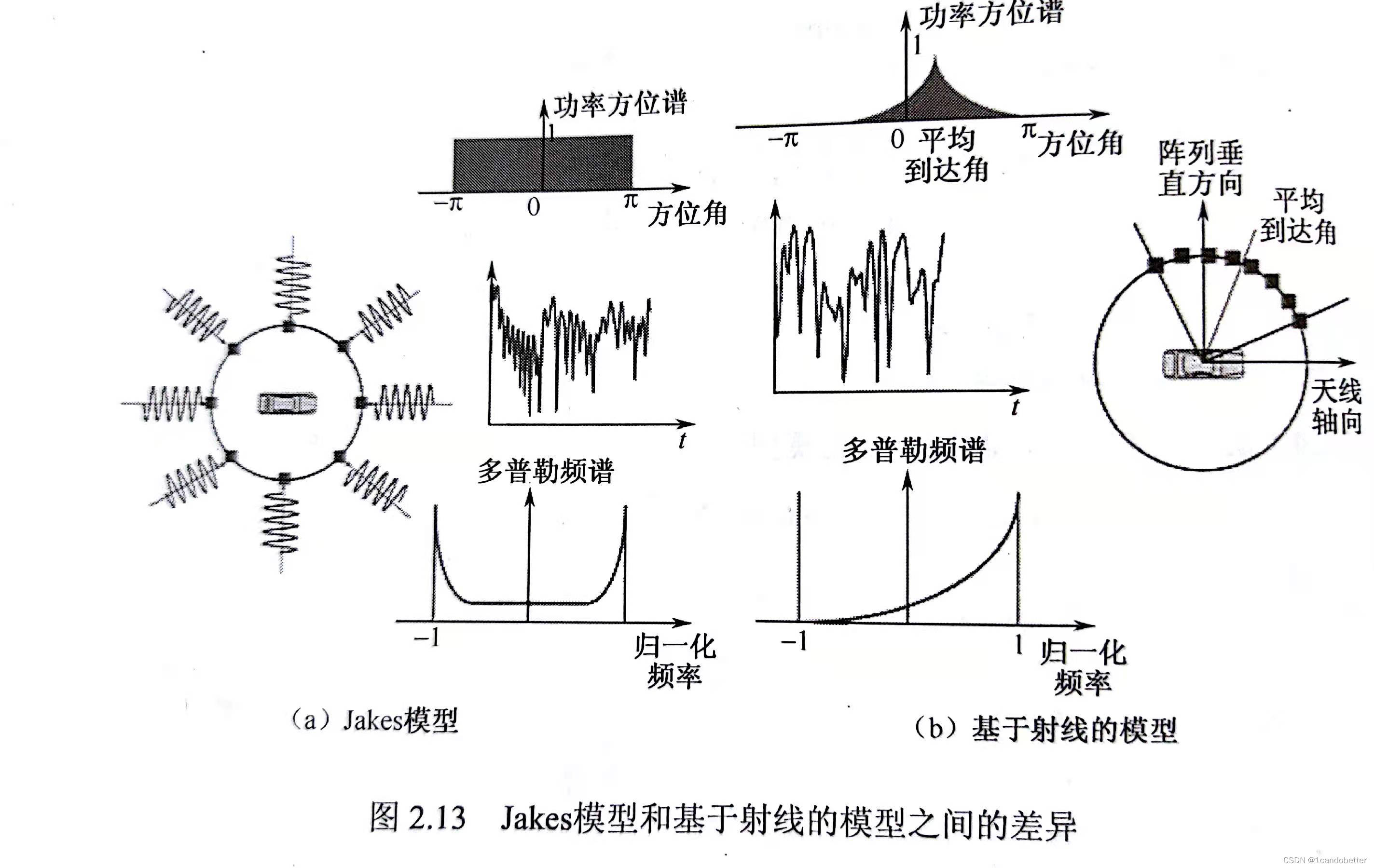
下图给出了基于射线的信道模型，即大家熟知的3GPP用于MIMO系统的空间信道（SCM）模型

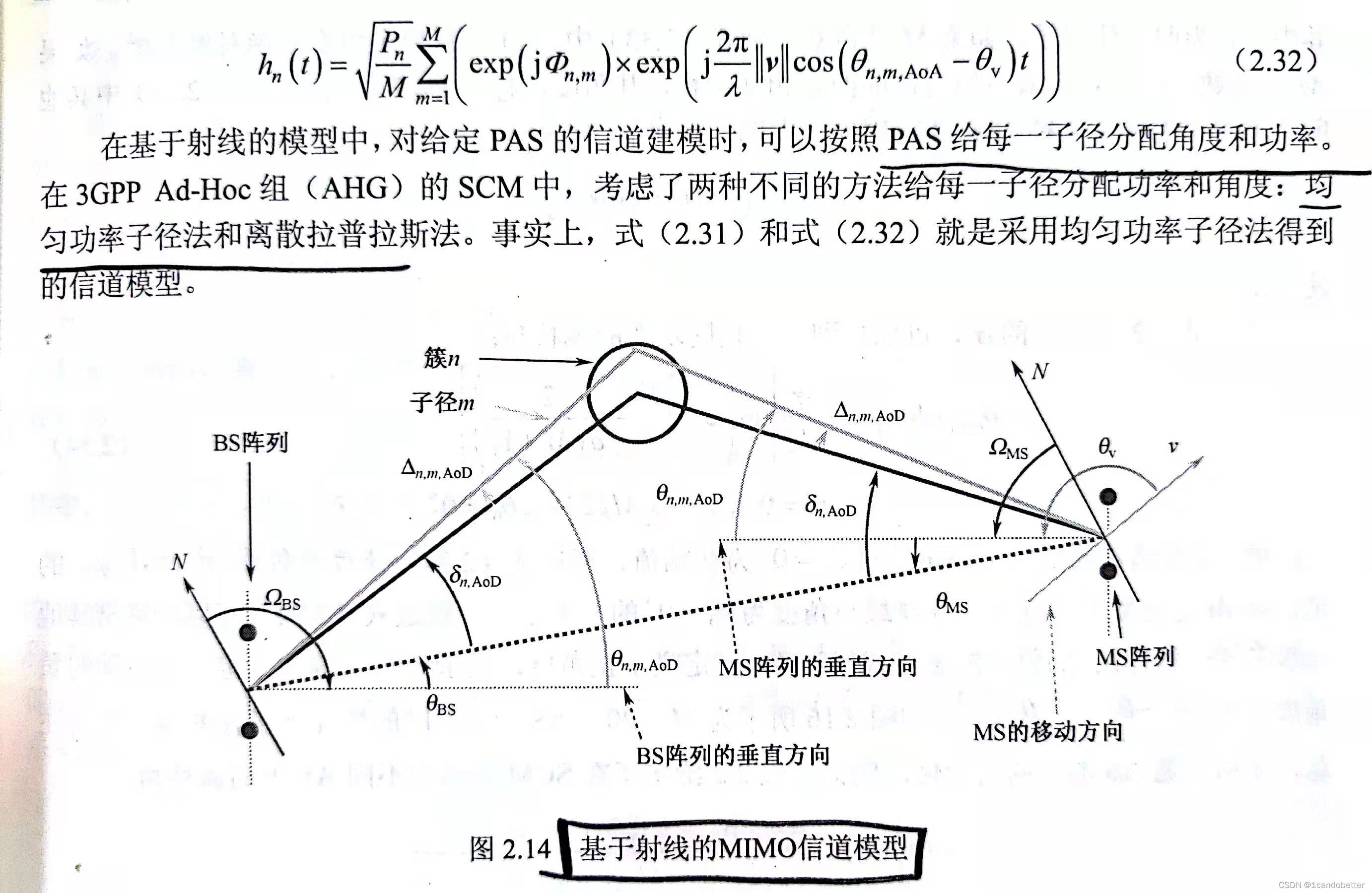
在基于射线的模型中，对给定PAS（功率方位谱）的信道建模时，可以按照PAS给每一子径分配角度和功率。考虑两种不同方法给每一子径分配功率和角度：均匀功率子径法和离散拉普拉斯法。

均匀功率子径法

均匀功率子径法为每一条子径分配相同的功率、不同的角度。等功率分配通常会简化建模的过程。给定子径数M，在确定的每一条子径的角度时，要使得由子径分割的PAS（功率方位谱）面积相同。下图描述了两条子径的情况，偏移角将PAS划分为三个不同的部分，每一部分面积相同。

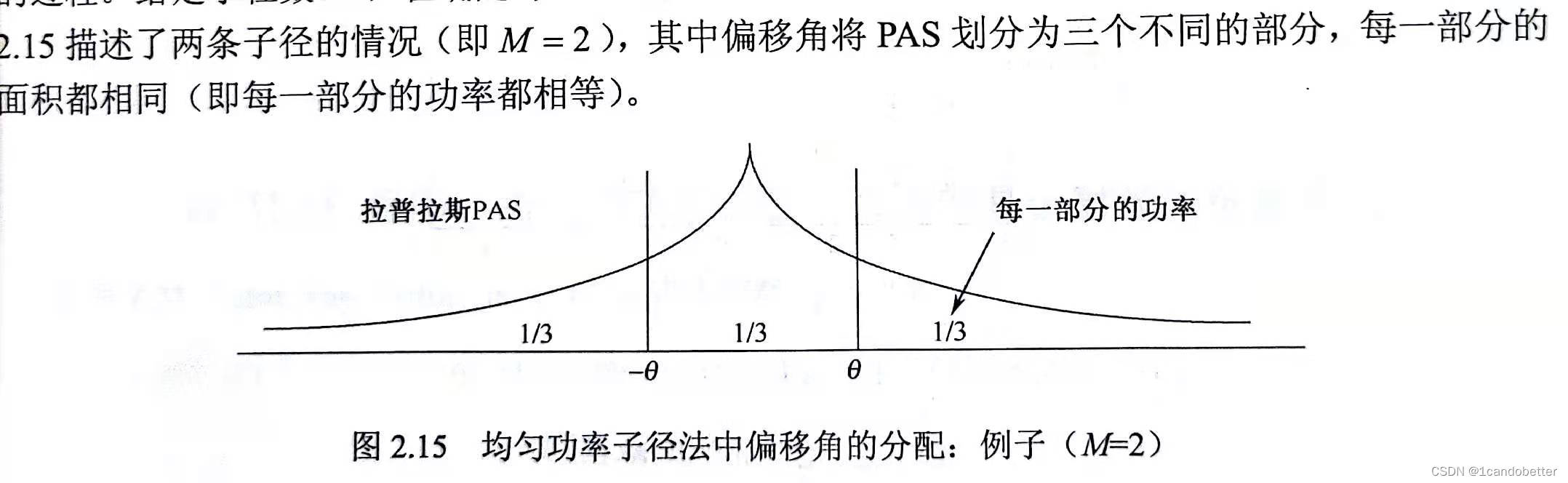
采样的拉普拉斯法

拉普拉斯子径法中，每一子径功率服从拉普拉斯PAS，偏移角渐进集中在平均AOA附近。

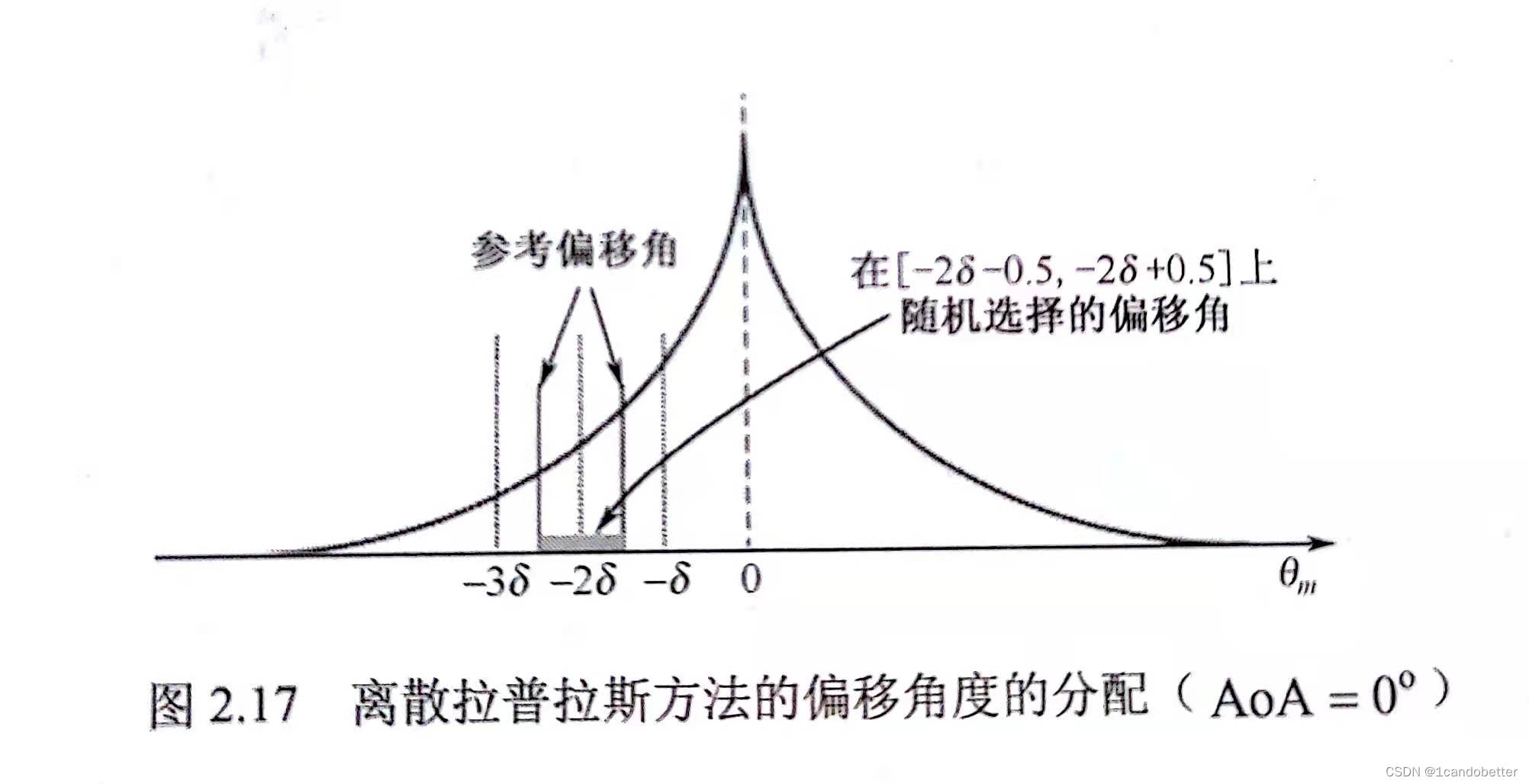
频率选择性衰落信道模型

对频率选择性衰落信道建模时,需要时延分布(PDP).PDP描述了接收信号的平均功率在每一径上的分布情况,其中每一径的功率由该径功率与第一径功率比值给出.

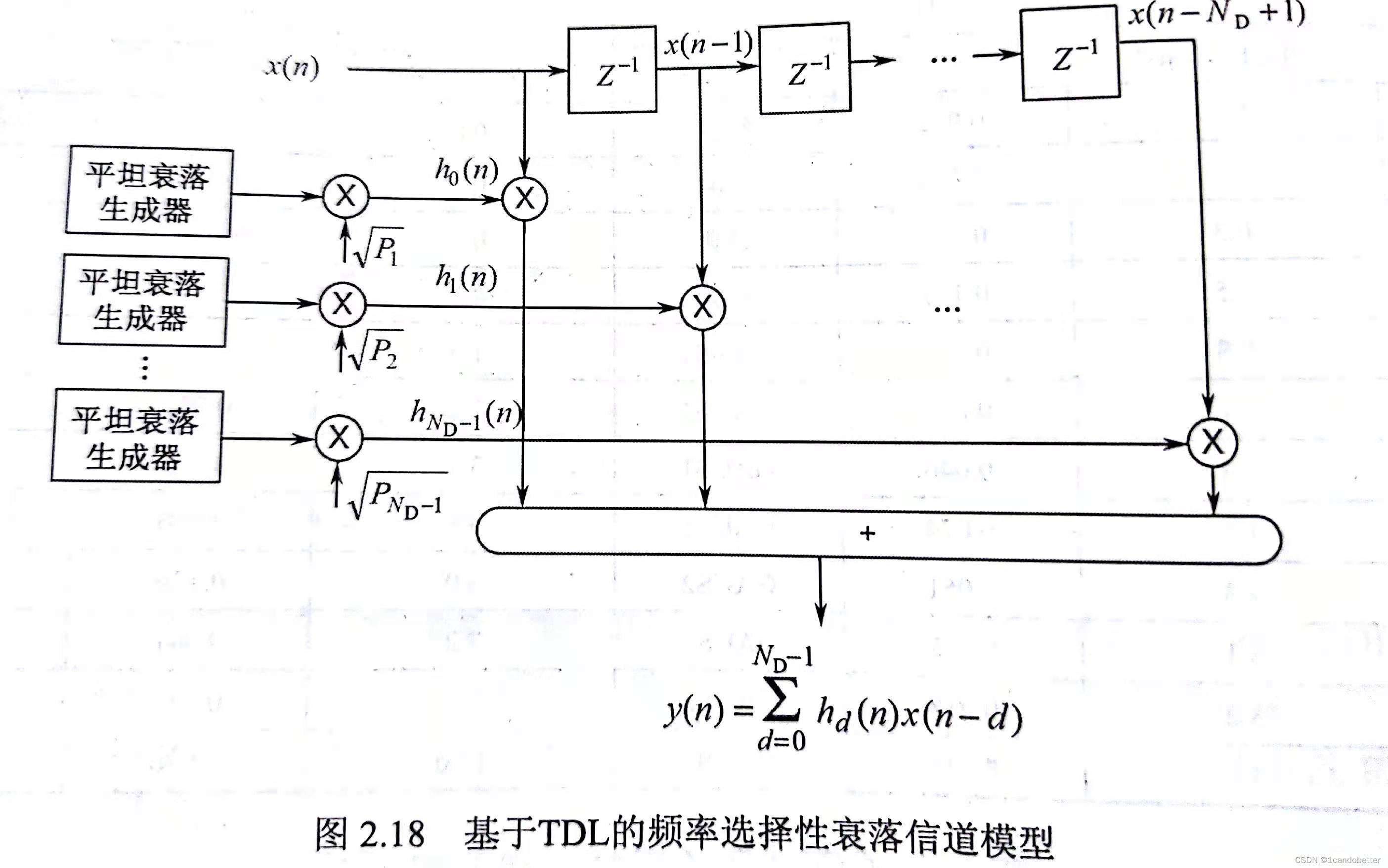
抽头延时线模型

通常利用抽头延迟线(TDL) 模型实现多径信道.TDL模型采用一组非频率选择性衰落生成器(如FWGN或者Jakes模型),其中各生成器相互独立,且平均功率为1.独立的衰落生成器的输出与抽头功率相乘,得到TDL模型的系数.实际上,可以用FIR滤波器实现TDL.

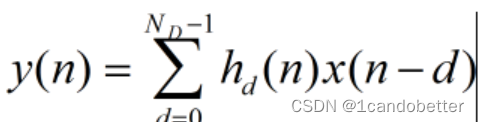
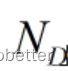为FIR滤波器的抽头数.然而如果抽头时延不是采样周期Ts的整数倍,就不能直接用FIR滤波器实现.

抽头调整

由于一般信道的PDP是基于特定环境的实际测量得到的,时延有可能不是采样周期的整数倍,在这种情况下为了实现离散的信道仿真器,需要调整PDP.例如,可以利用过采样将抽头时延修正为采样周期的整数倍,然而这样做会导致FIR滤波器的抽头数太多.反而抽头插值,取整或抽头重复采样是实施起来更为简便的方法.必须要保证抽头调整后信道的特性(如时延扩展RMS)保持不变