摄像机校准一般采用小孔成像模型,理想的小孔模型是线性模型,但是由于存在镜头畸变等原因,线性模型通常要加上一些内部参数,变成非线性模型。现对产生这一现象的原理以及解决方法进行整理,如下:
一、镜头畸变现象介绍
相机的成像过程实质上是坐标系的转换。首先空间中的点由 “世界坐标系” 转换到 “像机坐标系”,然后再将其投影到成像平面 ( 图像物理坐标系 ) ,最后再将成像平面上的数据转换到 图像像素坐标系。但是由于透镜制造精度以及组装工艺的偏差会引入畸变,导致原始图像的失真。镜头的畸变分为径向畸变和切向畸变两类。参见:
http://blog.csdn.net/dcrmg/article/details/52950141
http://blog.csdn.net/waeceo/article/details/50580808
1. 径向畸变
径向畸变是沿着透镜半径方向分布的畸变,产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲,这种畸变在普通廉价的镜头中表现更加明显,径向畸变主要包括桶形畸变和枕形畸变两种。
成像仪光轴中心的畸变为0,沿着镜头半径方向向边缘移动,畸变越来越严重。畸变的数学模型可以用主点(principle point)周围的泰勒级数展开式的前几项进行描述,通常使用前两项,即k1和k2,对于畸变很大的镜头,如鱼眼镜头,可以增加使用第三项k3来进行描述,成像仪上某点根据其在径向方向上的分布位置,调节公式为:
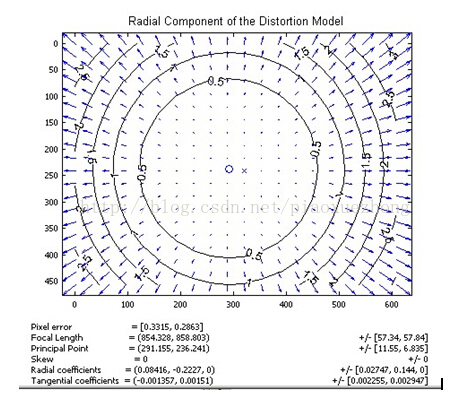
式里(x0,y0)是畸变点在成像仪上的原始位置,(x,y)是畸变较真后新的位置,下图是距离光心不同距离上的点经过透镜径向畸变后点位的偏移示意图,距离光心越远,径向位移越大,表示畸变也越大,在光心附近,几乎没有偏移。
2. 切向畸变
切向畸变是由于透镜本身与相机传感器平面(成像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。畸变模型可以用两个额外的参数p1和p2来描述:
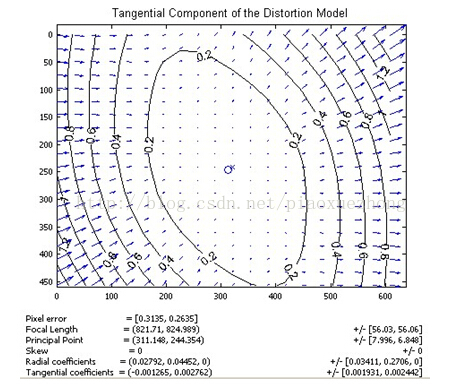
大体上畸变位移相对于左下——右上角的连线是对称的,说明该镜头在垂直于该方向上有一个旋转角度。
二、物象坐标映射转换
opencv中,函数findhomography可以找到这一单应性矩阵。
Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,
Mat& status, int method=0,
double ransacReprojThreshold=3 );
Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,
vector<uchar>& status, int method=0,
double ransacReprojThreshold=3 );
Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,
int method=0, double ransacReprojThreshold=3 ); 1、srcPoints,dstPoints为CV_32FC2或者vector<Point2f>类型
2、method:0表示使用所有点的常规方法;CV_RANSAC 基于RANSAC鲁棒性的方法;CV_LMEDS 最小中值鲁棒性方法
3、ransacReprojThreshod 仅在RANSAC方法中使用,一个点对被认为是内层围值(非异常值)所允许的最大投影误差。如果srcPoints和dstPoints单位是像素,通常意味着在某些情况下这个参数的范围在1到10之间。
4、status,可选的输出掩码,用在CV_RANSAC或者CV_LMEDS方法中。注意输入掩码将被忽略。
如果参数method设置为默认值0,该函数使用一个简单的最小二乘方案来计算初始的单应性估计。然而,如果不是所有的点对(srcPoints,dstPoints)都适应这个严格的透视变换。(也就是说,有一些异常值),这个初始估计值将很差。在这种情况下,我们可以使用两个鲁棒性算法中的一个。RANSCA和LMEDS这两个方法都尝试不同的随机的相对应点对的子集,每四对点集一组,使用这个子集和一个简单的最小二乘算法来估计单应性矩阵,然后计算得到单应性矩阵的质量quality/goodness。(对于RANSAC方法是内层围点的数量,对于LMeDs是中间的重投影误差)。然后最好的子集用来产生单应性矩阵的初始化估计和inliers/outliers的掩码。
三、相机校正
在第二部分,求得的单应性矩阵,是由两部分构成的:内参矩阵和外参矩阵,在OpenCV的3D重建中,对摄像机的内参外参有讲解:
外参:摄像机的旋转平移属于外参,用于描述相机在静态场景下相机的运动,或者在相机固定时,运动物体的刚性运动。因此,在图像拼接或者三维重建中,就需要使用外参来求几幅图像之间的相对运动,从而将其注册到同一个坐标系下面来。
内参:下面给出了内参矩阵,需要注意的是,真实的镜头还会有径向和切向畸变,而这些畸变是属于相机的内参的。
摄像机内参矩阵:
fx s x0
K = 0 fy y0
0 0 1其中,fx,fy为焦距,一般情况下,二者相等,x0、y0为主点坐标(相对于成像平面),s为坐标轴倾斜参数,理想情况下为0。
摄像机外参矩阵:包括旋转矩阵和平移矩阵,旋转矩阵和平移矩阵共同描述了如何把点从世界坐标系转换到摄像机坐标系。
旋转矩阵:描述了世界坐标系的坐标轴相对于摄像机坐标轴的方向。
平移矩阵:描述了在摄像机坐标系下,空间原点的位置。
博文http://blog.csdn.net/dcrmg/article/details/52939318中给出了opencv校正流程,表示感谢.
另外还可以参见:
http://www.cnblogs.com/tianya2543/p/3894644.html,http://www.eepw.com.cn/article/201706/352360.htm
http://blog.csdn.net/dcrmg/article/details/52929669
1. 准备标定图片
标定图片需要使用标定板在不同位置、不同角度、不同姿态下拍摄,最少需要3张,以10~20张为宜。标定板需要是黑白相间的矩形构成的棋盘图,制作精度要求较高,如下图所示:
2.对每一张标定图片,提取角点信息
需要使用findChessboardCorners函数提取角点,这里的角点专指的是标定板上的内角点,这些角点与标定板的边缘不接触。
findChessboardCorners函数原型:
//! finds checkerboard 








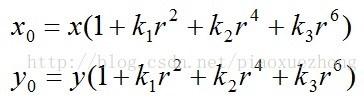
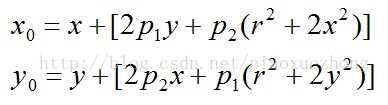

 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








