目录
SAS是统计学工具,帮助人们计算一些有明确公式但是计算复杂的值,节省人力,便于人们对数据进行分析。
语句分为两种:数据步和过程步。我的理解是让SAS处理数据首先要让它清楚数据有哪些(几个自变量),之后清楚要传递出来的有哪些(散点图、曲线、F-检验......)
可以先在txt中写,再复制粘贴。word有些时候报错。
回归分析:
了解变量之间是否相关,相关方向与强度,建立因变量Y与自变量X之间关系的模型,预测感兴趣的变量,观察事物的发展趋势,并进行控制。
分为数据步(DATE)和过程步(PROC)
一、一元线性回归
1. 相关说明
若分析自变量X与因变量Y的内在联系,X是确定性的变量,Y是随机性的变量,进行n次独立试验,测得数据如下
| X | x1 | x2 | ...... | xn |
| Y | y1 | y2 | ...... | yn |
回归模型:Y=a+bX+ (E(
)=0,Var(
)=,Cov(
)=0)
用最小二乘法估计参数 min (不能直接相减求和,因为相减结果有正有负,要进行平方。求:一阶导数为零)
一元线性回归模型的显著性检验:(只做其中之一个就好)
1.回归方程的显著性检验(F-检验)
2.回归系数的显著性检验(t-检验)
3.相关系数的显著性检验(判定系数,相关系数 r)
2. 一元线性实例
PROC REG 输入数据集名 <选项列表> ;
MODEL dependents=independents / <选项列表> ;
其它选择语句 ;
RUN;
代码及解释
(求线性回归方程,并做显著性检验,若x=2,求y的0.95置信区间)
/*数据步*/
data ex; /*表示数据集为ex*/
input x y @@; /*@@表示续行符*/
cards;
1.5 4.8 1.8 5.7 2.4 7 3 8.3 3.5 10.9 3.9 12.4 4.4 13.1 4.8
13.6 5 15.3 2 . /*. 用于预测,与前面的数字用空格隔开*/
;
/*过程步*/
proc gplot; /*画散点图*/
plot y*x; symbol i=rl v=dot; /*全程控制语句,连线方式是带上下界的回归线,点的形状是实心圆点,
“c=”可用来表示颜色*/
proc reg; model y=x/cli ;
run;1./* */为解释语句
2.SAS以;为结尾
3.如果没有续行符@@也可以(表示一行数据中只读x y两个数,于是)数据要一行一行的输。1.5 4.8 回车 1.8 5.7
4.“2 .”的意思:所给数据中没有当x=2时y的值,预测值用. 但是注意数字与.之间有空格。
5.数据步和过程步一般都有run,但是在最后过程步有run,就合并了。
6.proc用于执行任务,其中gplot是散点图(不是缩写),reg是回归;意思是做出散点图(或回归线)
7.plot y*x:说明y是纵坐标,x是横坐标。i是这些点的连线方式,rl是回归直线;spline是光滑曲线。即做一条直线(或光滑曲线)
8.v是线上点的形状,dot是实心圆点;plus是加号;
9.c是线的颜色,直接blue,red 就好。
10.model y=x 是说通过一条直线描述因变量y和自变量x之间的关系。cli是输出每个个体观测值95%置信区间的上、下限。noint是说拟合出没有常数项(截距)的回归模型
结果及解读
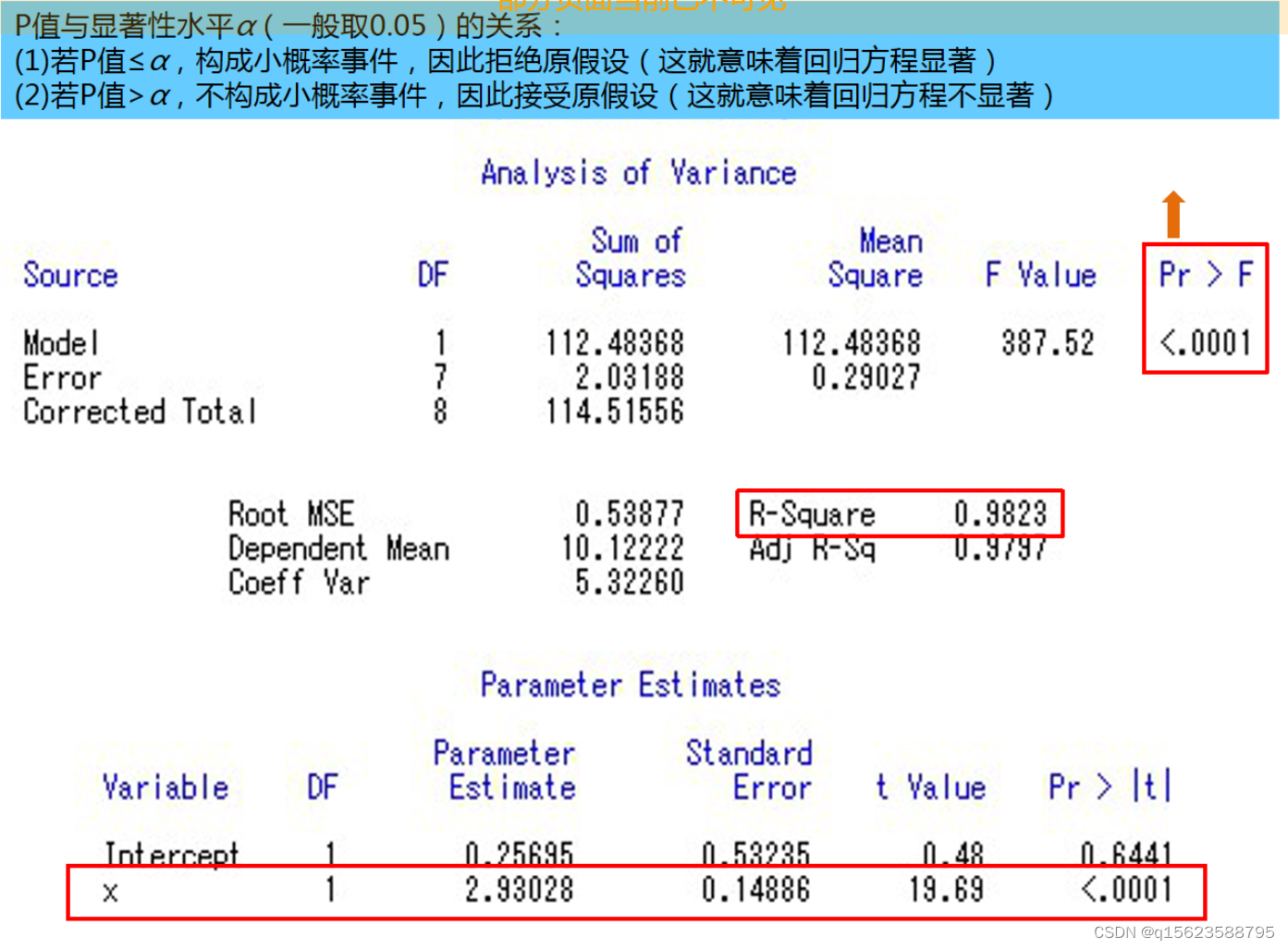
1.source为误差来源,其中Model是模型所带来的误差SSA,自由度DF是1,大小是112.48368,均方MSA是112.48368;Error是随机误差SSE,自由度是7,大小是2.03188,均方MSE是0.29027;Total是总离差平方和SST=SSA+SSE。F值是MAS除以MSE,大小为387.52。显著性检验Pr>F的值要小于0.05()
2.R-Square是,Adj R-Sq是修正
,与R方相比,Adj R-Sq更加稳健,因为它考虑了模型中自变量的个数,避免了因自变量个数过多而导致的模型过度拟合。
3.Intercept行中ParameterEstimate是截距a的值,x是系数b的值,所以结果是Y=2.93028x+0.25695.

其中输入数据仅9对,第十行为预测值,当x=2时y=6.1175(其余如图)
二、一元非线性回归
1. 相关说明
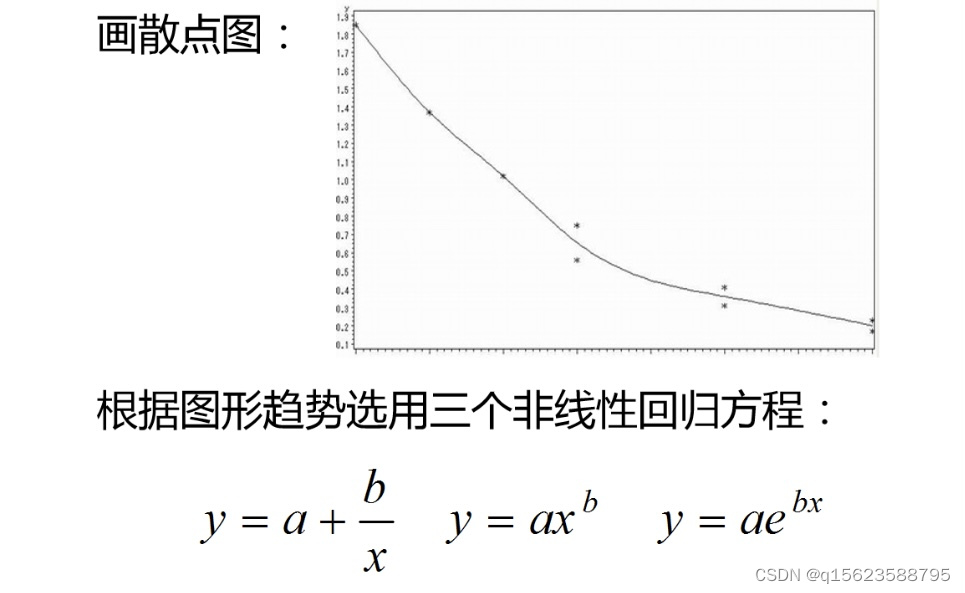
常见的非线性回归方程
;
;
;
;
思想:转化为线性规划

曲线方程有多个,不确定是哪一个,所以先画散点图选定方程,有时会出现遗漏现象,可以用泰勒公式(matlab)。例如:
2. 一元非线性实例

data ex; input x y @@;
x1=1/x; lx=log(x);ly=log(y);
cards;
1 1.85 2 1.37 3 1.02 4 0.75 4 0.56
6 0.41 6 0.31 8 0.23 8 0.17
;
proc gplot; plot y*x; symbol i=spline v=star;
proc reg;model y=x1;
proc reg;model ly=lx;
proc reg;model ly=x;
run;代码大意:画一个散点图,y是纵轴,x是横轴,光滑曲线,点用星星点,做这三个模型的回归分析
注意,输入的还是x和y的值,只是最后画图不是。model直线需要更换。
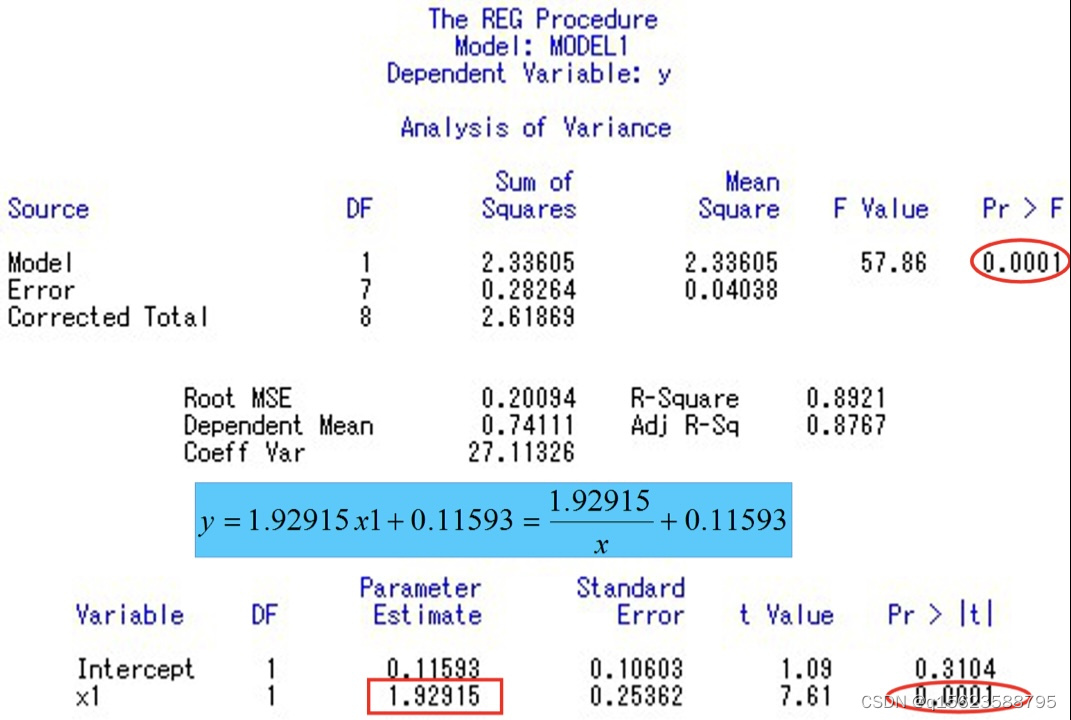
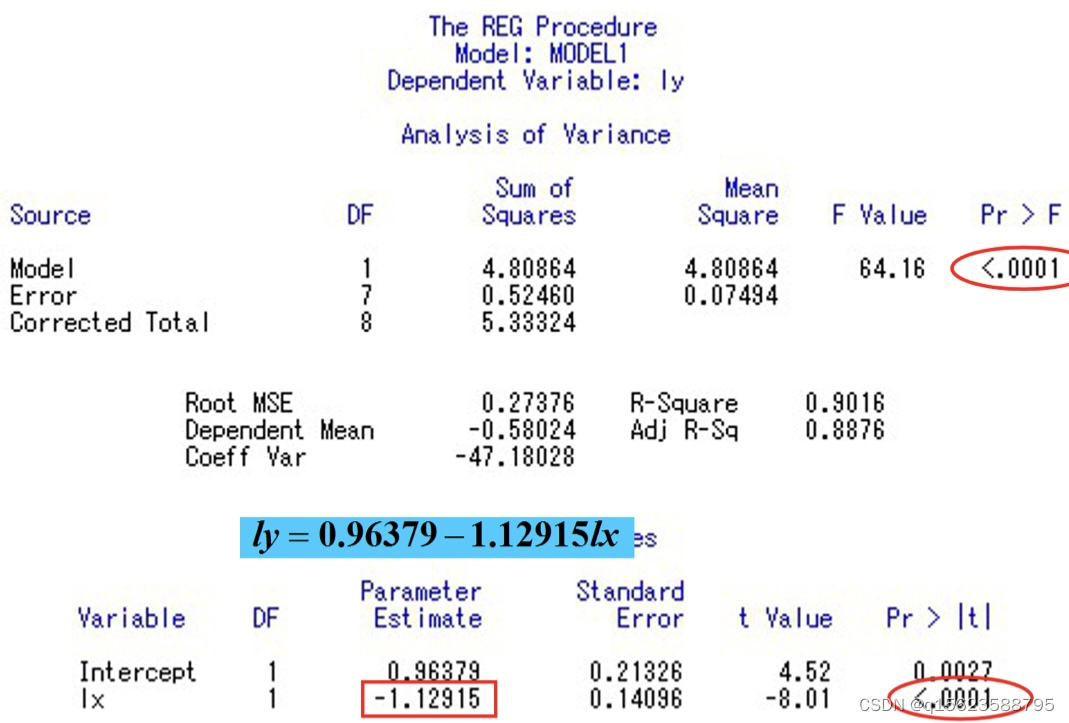

在得到结果后要进行检验以最终确定是哪个模型
检验就是看那个拟合效果好,预测出来的值和实际值相差不大,所以求出预测值和实际值的差异,由于差异有正有负且不能相互抵消,所以要求出剩余平方和,越小越好。
程序如下,
data ex; input x y @@;
x1=1/x;lx=log(x);ly=log(y);
y1=1.9291*x1+0.11593; q1+(y-y1)**2;
y2=exp(0.9638-1.1292*lx); q2+(y-y2)**2;
y3=exp(0.9230-0.3221*x); q3+(y-y3)**2;
cards;
1 1.85 2 1.37 3 1.02 4 0.75 4 0.56
6 0.41 6 0.31 8 0.23 8 0.17
;
proc print;var q1-q3; run;q1+(y-y1)**2就是q1=q1+(y-y1)**2;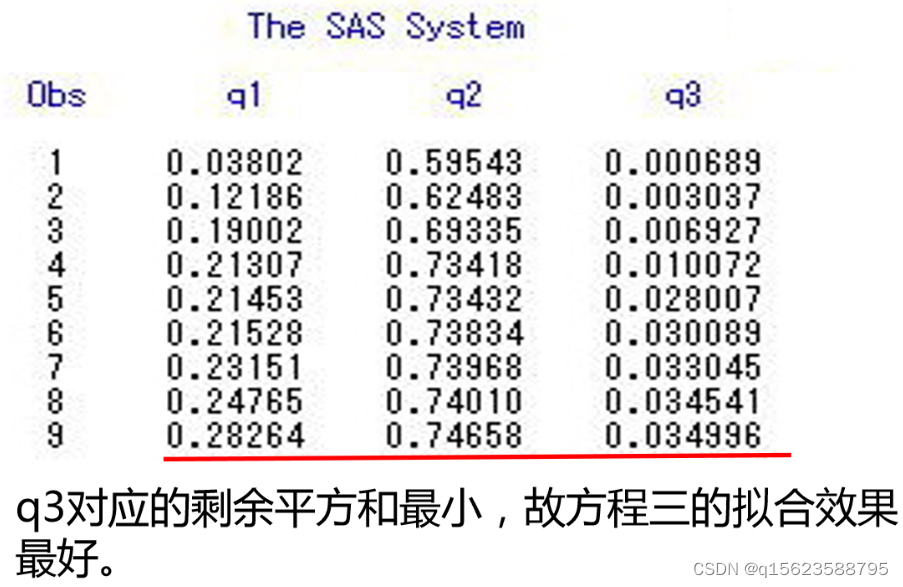
三、多元回归
因为变量多了,画图所需要的维数也多,就没有画图的方法。所以直接建模型,根据检验结果决定是哪一个模型。
1. 相关说明
1.1多元线性回归模型的假设
>解释变量是确定性变量,不是随机变量
>解释变量之间互不相关,即无多重共线性
>随机误差项不存在序列相关关系
>随机误差项与解释变量之间不相关
>随机误差项服从O均值、同方差的正态分布
1.2多元线性回归模型的检验
1.拟合优度检验(判定系数)
2.回归方程的显著性检验(F -检验)
3.回归参数的显著性检验(t-检验)
注意:对多元线性回归而言,这三种检验考虑的问题不同,并不等价,需分别检验。
1.拟合优度检验
目的:构造一个不含单位,可以相互比较,而且能直观判断拟合优劣的指标。
判定系数的定义:
意义:判定系数越大,自变量对因变量的解释程度越高,自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。
取值范围:0-1
2.回归方程的显著性检验
检验的目的:检验Y与解释变量X1,X2,...,Xk之间的线性关系是否显著。
原假设:
备择假设:不全为0(i=1,2,...,k)
计算统计量:,
拒绝H0,回归方程显著。
3.回归系数的显著性检验
回归方程显著,并不意味着每个解释变量对因变量Y的影响都重要,因此需要进行检验。
原假设:(i=1,2,......,k)
备择假设:(i=1,2,......,k)
计算统计量:,
拒绝原假设
拓展:方差膨胀因子(Variance Inflation Factor,VIF)是一种用于评估多元线性回归模型中多重共线性问题的指标。多重共线性是指自变量之间存在高度的相关性,使得回归系数的估计不准确。
VIF是用来度量多元线性回归模型中每个自变量与其他自变量之间的相关性的指标。它可以用来评估自变量之间的线性相关性,以及自变量与其他自变量之间的相关性的影响。
VIF = 1 / (1 - R\_i^2)
其中,R\_i^2 是自变量 X\_i 与其他自变量的残差平方和的比例,即 R\_i^2 是自变量 X\_i 的回归系数的 determination coefficient(决定系数)。
VIF的值的范围是 [1, +∞)。当 VIF 值接近 1 时,表明该变量与其他变量 basically uncorrelated,也就是不存在多重共线性问题。当 VIF 值较大(通常认为 VIF 值大于 10 时)时,表明该变量与其他变量存在高度的相关性,可能会导致多重共线性问题。
在进行多元线性回归分析时,可以使用 VIF 来评估自变量之间的相关性,并采取适当的变量选择方法来解决多重共线性问题。例如,可以删除 VIF 值最大的变量,或者使用主成分分析(Principal Component Analysis,PCA)等技术来降维。
2. 多元回归实例1

data ex; /*表示数据集为ex*/
input x1 x2 y @@;
cards;
1.37 9.08 4.93 11.34 1.89 1.86 9.67 3.06 2.33 0.76
10.2 5.78 17.67 0.05 0.06 15.91 0.73 0.43 15.74
1.03 0.87 5.41 6.25 3.86 5.4 6.3 . /*预测*/
;
proc reg; /*调用回归模块*/
model y=x1 x2/cli; /*对y关于x1,x2做回归,
/cli表示要求预测区间*/
run;预估x1=5.4,x2=6.3时y的值
方程显著性检验(F检验)

F value=392.52,pr>F的值<0.0001,远小于0.05,故拒绝原假设,接受备择假设,认为y1与x1,x2之间具有显著性的线性关系;
参数显著性检验(t检验)

由参数估计表可知,对自变量x2检验t值为t=2.12,Pr>|t|的值=0.0879,大于0.05,因此,接受原假设,认为x2的系数应为0。为此,需要在程序中model y1=x1x2中去掉x2 .
修改SAS程序
model y=x1 x2 → model y=x1 得到:

对常数检验t值分别为t=33.9、,Pr>|t|的值<0.0001,远小于0.05,说明截距项通过检验,估计值为5.62117,同理可知 x1的系数通过检验,估计值为-0.31911
所以 回归方程: y = -0.31911* x1 + 5.62117
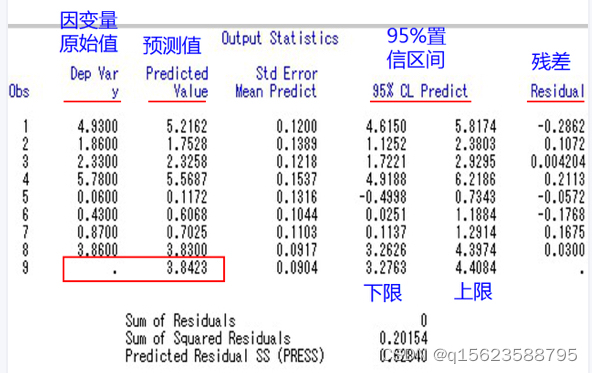
3. 多元回归实例2
湖北省油菜投入与产出的统计分析
说明:
1.投入指标:(1)土地(S);(2)劳动(L);(3)资本(K)
2.产出指标:用湖北省历年油菜生产的总产量(V)来表示。
3.模型:。转化为
。
代码
data ex; input y k s l t @@;
x1=log(k); x2=log(s); x3=log(l) ; y1=log(y);
cards;
70.8972 40076.5884 825.1305 15347.4273 1
83.7506 48008.7690 915.1500 15832.0950 2
70.8627 44593.8425 801.6150 13306.8090 3
78.3451 43460.3229 783.2100 13314.5700 4
98.0749 72657.2633 923.8050 14596.1190 5
134.8767 146108.3421 1282.8900 20911.1070 6
147.5315 162433.3500 1244.7000 18670.5000 7
154.7607 166979.6325 1330.5150 18627.2100 8
159.9743 190395.5262 1505.4600 20775.3480 9
198.4942 205914.6645 1738.4100 22599.3300 10
194.7943 189762.7335 1677.0900 20963.6250 11
187.1013 193461.5610 1761.9450 21936.2153 12
235.1184 183768.4035 1779.1500 19606.2330 13
;
proc reg; model y1=x1 x2 x3 t ;
run;结果及解读
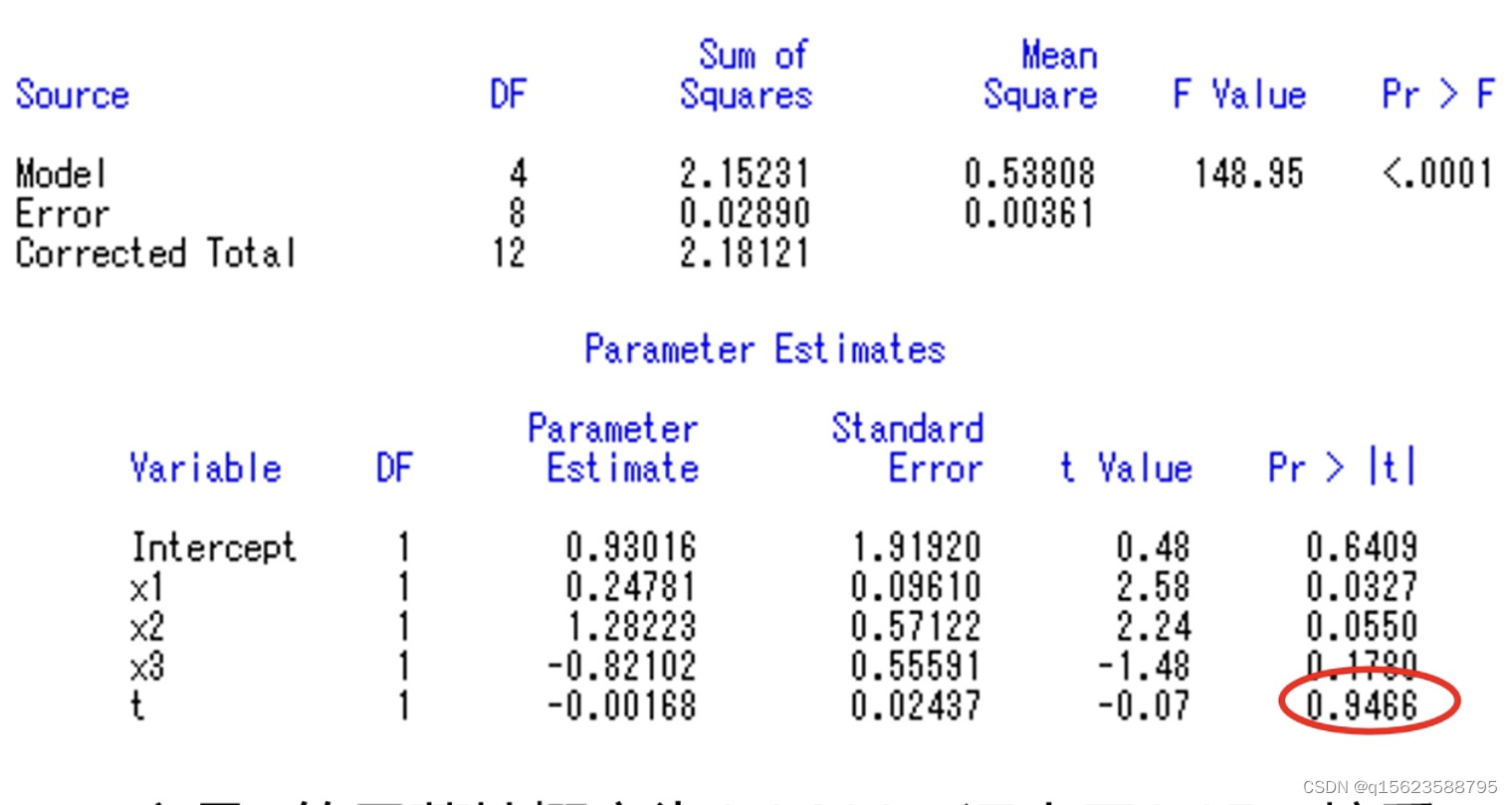
变量t 的显著性概率为0.9466,远大于0.05,接受原假设,认为t不显著,因此将程序中model y1=x1 x2 x3 t中去掉t,即改为model y1=x1 x2 x3.即先把最不显著的变量消掉,但不能所有不显著的变量都一起删,删除一个变量之后,另一个变量的显著性检验可能会由不显著变为显著,需要再跑一次程序。(记住这一步,下文要用到)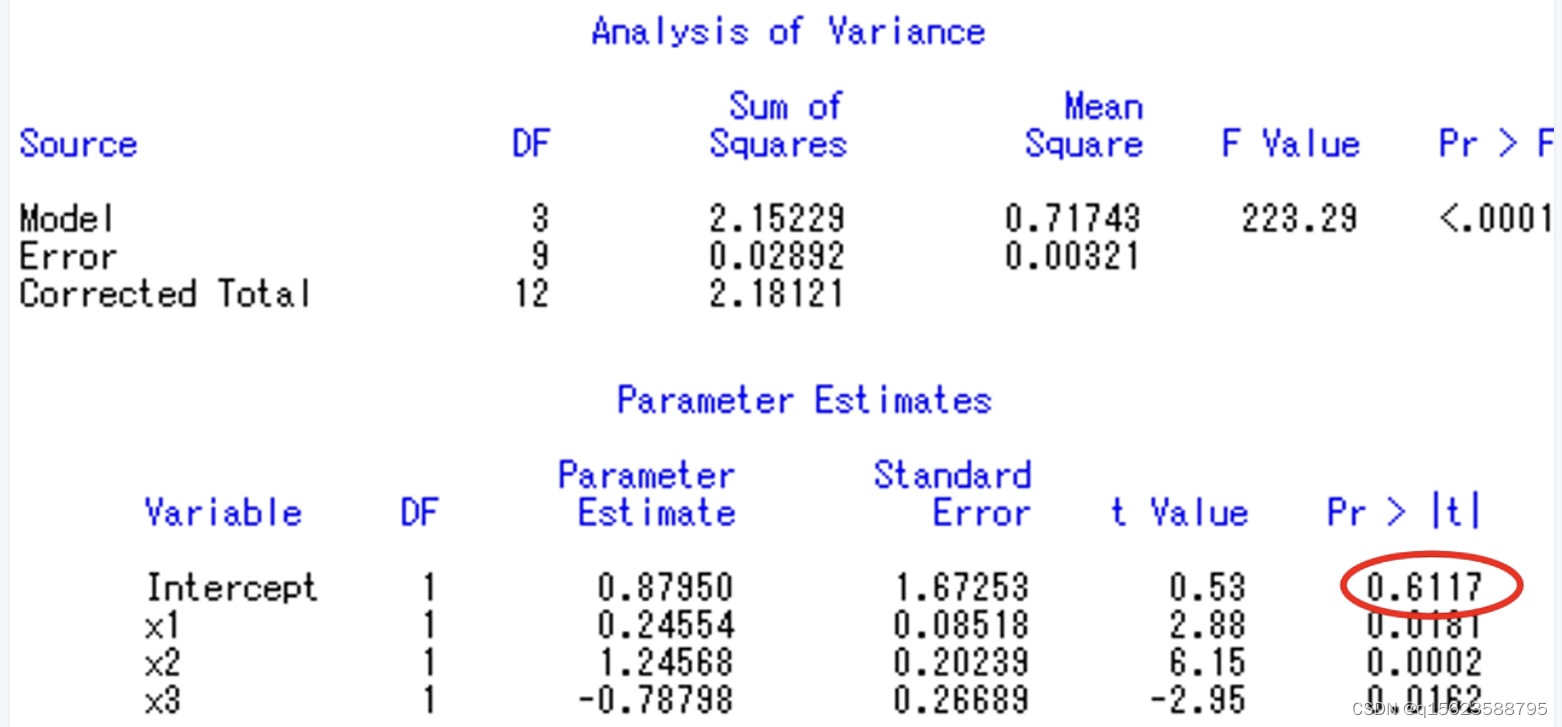
截距项intercept 的显著性概率为0.6117,大于0.05,因此将程序中model y1=x1 x2 x3 改为model
y1=×1 x2 x3 /noint:意思是不要截距项(因为截距项的显著性检验0.6117>0.05没通过)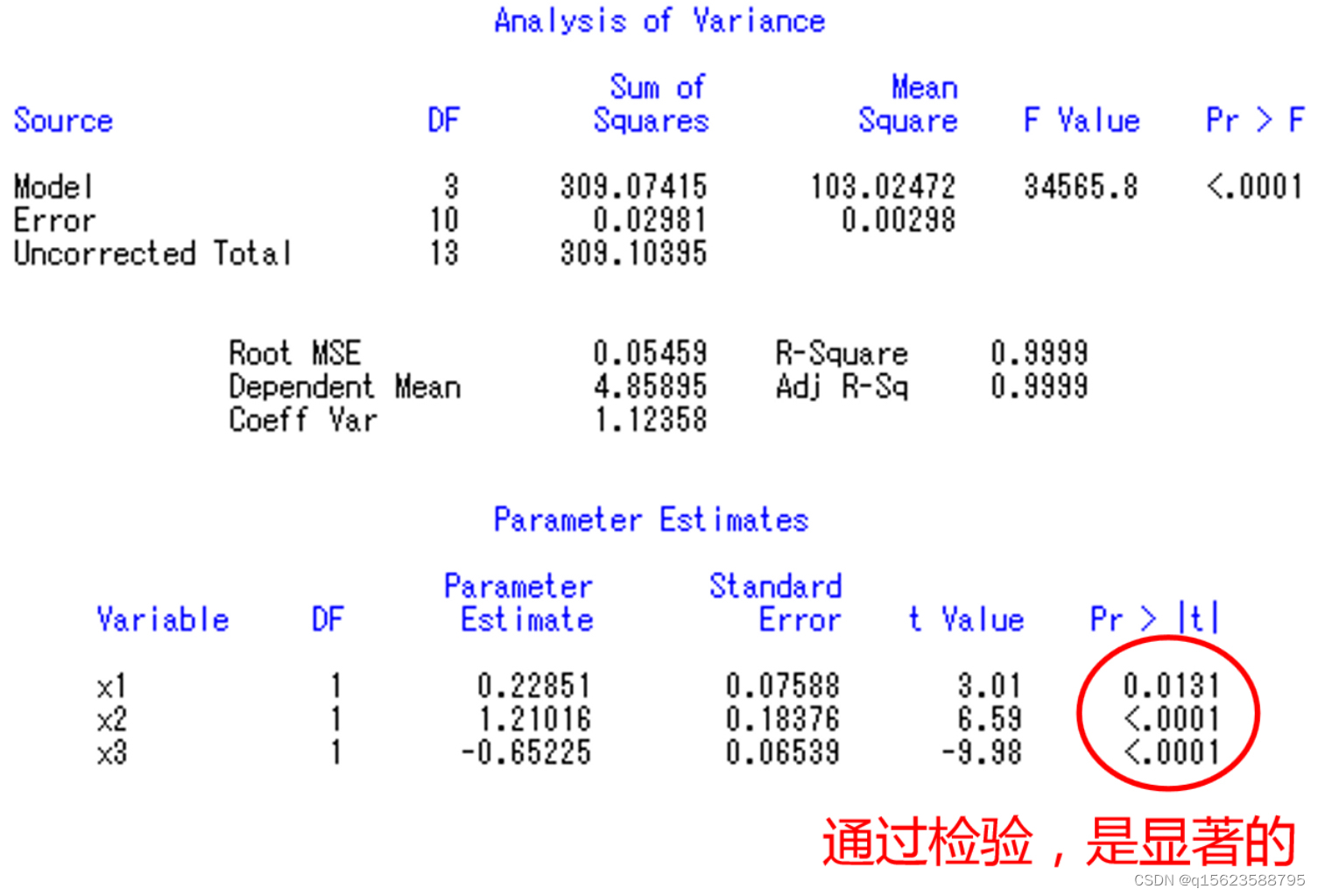
写出结果:
即最后结果为
但是根据经济学知识得知此模型虽然满足数学规则,但不能通过经济检验()。
四、逐步回归
1. 相关说明
基本思想:(先看作只有一个变量x1,对他进行数据步过程步,并对其进行检验,结果如果是显著就留下,不显著就扔掉。之后向里增加变量x2,在x1被留下的基础上,对Y进行有两个自变量x1x2的数据步过程步若x1x2都显著留下,不显著扔掉;在x1扔掉的基础上,对x2进行类似x1的过程,x3以此类推)
书面语:将变量一个一个引入,引入的条件是其偏回归平方和经检验是显著的。同时,每引入一个新变量后,对已入选回归模型的老变量逐个进行检验,将经检验认为不显著的变量删除,以保证所得自变量子集中每一个变量都是显著的。此过程经过若干步直到不能再引入新变量为止。
目的:从大量可能有关的自变量中挑选出对因变量有显著影响的部分自变量。
为了筛选变量宽容,程序中默认显著度为0.15 而不是0.05,以避免条件过于严格只用筛选无法进行。自变量进入模型的顺序并不反映它们的重要程度。 逐步回归选择变量快捷,但对于存在多重共线的自变量选择,有时并不准确,使用时注意分辦。代码为model....../selection=stepwise
2. 逐步回归实例
代码:湖北省油菜投入与产出的统计分析
data ex; input y k s l t @@;
x1=log(k); x2=log(s); x3=log(l) ; y1=log(y);
cards;
70.8972 40076.5884 825.1305 15347.4273 1
83.7506 48008.7690 915.1500 15832.0950 2
70.8627 44593.8425 801.6150 13306.8090 3
78.3451 43460.3229 783.2100 13314.5700 4
98.0749 72657.2633 923.8050 14596.1190 5
134.8767 146108.3421 1282.8900 20911.1070 6
147.5315 162433.3500 1244.7000 18670.5000 7
154.7607 166979.6325 1330.5150 18627.2100 8
159.9743 190395.5262 1505.4600 20775.3480 9
198.4942 205914.6645 1738.4100 22599.3300 10
194.7943 189762.7335 1677.0900 20963.6250 11
187.1013 193461.5610 1761.9450 21936.2153 12
235.1184 183768.4035 1779.1500 19606.2330 13
;
proc reg;model y1=x1 x2 x3 t/selection=stepwise;
run;结果及解读
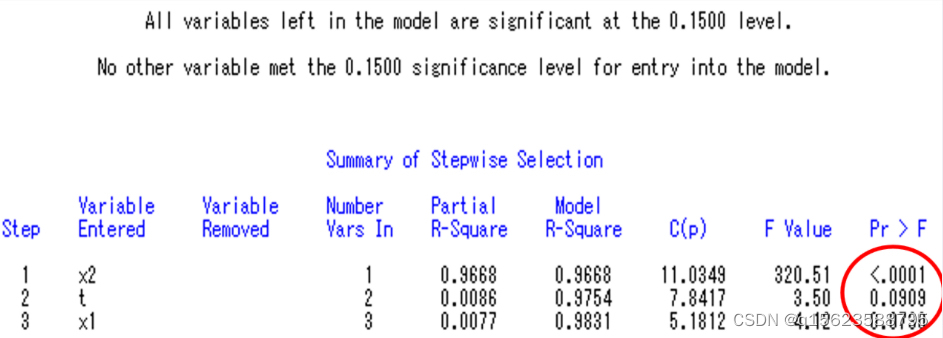
从程序结果中不难看出,x2、x1、t进入模型。因此程序中model y1=x1 x2 x3 t /selection=stepwise;改为model y1=x1 x2 t /noint;再运行一遍即可得到以下的结果: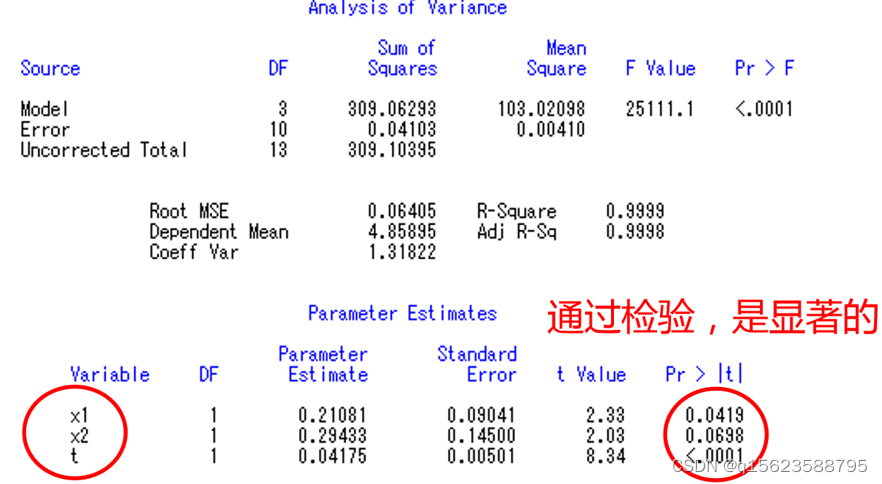
此时注意逐步回归方法(一个一个的往里填检验结果显性的变量)得到结果与上文多元回归部分(一起做检验后依次删掉最不显著的)不同,其原因最有可能为有多重贡献性(即自变量之间是相关的),于是为了结果更加准确采用逐步回归方法。
五、标准化回归
看哪个自变量对因变量的影响最大,看最后得到的等式中哪个自变量前的系数最大,但是
由于单位量纲(如米和千米)不一样,偏回归系数的大小不能完全反映自变量对因变量影响的大小。要想真实反映自变量的贡献(谁对因变量的影响最大),标准化回归是个好的选择。
标准化回归方程,就是将自变量、因变量都标准化后建立的回归方程。(标准化:滅去均值,除以标准差),代码是model ........../stb
标准化回归系数(Beta值)在多元回归中被用来比较变量间的重要性。

从最后一列(标准化回归系数)可看出,x1重要性超过x2和t。与原先的参数大小比有变化。原回归系数X2最大。
























 1396
1396

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








